Complete Solutions to JEE ADVANCED (COMPREHENSION TYPE QUESTIONS) of chapter उष्मागतिकी तथा उष्मारसायन of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | उष्मागतिकी तथा उष्मारसायन |
| ERRORLESS HINDI | JEE ADVANCED (COMPREHENSION TYPE QUESTIONS) |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
निश्चित ताप पर अभिक्रिया की मानक गिब्स ऊर्जा `(Delta_r G^@)` का परिकलन `Delta_r G^@ = Delta_r H^@ - T.Delta_r S^@` से कर सकते है तथा अभिक्रिया के लिए तापमान के साथ `Delta_r H^@` तथा `Delta_r S^@` के मान में परिवर्तन को निम्न प्रकार परिकलित किया जा सकता है
`Delta_r H_(T_2)^@ - Delta_r H_(T_1)^@ = Delta_r C_p^@ (T_2 -T_1)`
` Delta_r S_(T_1)^@ - Delta_r S_(T_1)^@ = Delta_r C_p^@ ln(T_2/T_1)`
`Delta_r G^@ = Delta_r H^@ - T Delta_r S^@`
`Delta_r G^@ =-RT ln K_(eq)` द्वारा
निम्न अभिक्रिया पर विचार करें
`CO(g) +2H_2(g) iff CH_3OH(g)`
दिया है :`Delta_f H^@ (CO, g) = -114`kJ/mole
`S^@ (CH_3OH, g) = 240 "J/K mol" , C_(p,m)^@(H_2,g) = 29JK^(-1) "mol"^(-1)`
`S^@ (CO,g) = 198 "J/mol" -K , C_(p,m)^@ (H_2) = 28.8 ` J/mole - K
`C_(p,m)^@ (CO) = 29.4 `J/mol - K , `C_(p,m)^@ (CH_3OH) = 44 `J/mol-K
तथा `ln (320/300) = 0.06 ` , सभी आँकड़े 300K पर है।
300K ताप पर अभिक्रिया के लिए `Delta_r S^@` है
View Solutionनिश्चित ताप पर अभिक्रिया की मानक गिब्स ऊर्जा `(Delta_r G^@)` का परिकलन `Delta_r G^@ = Delta_r H^@ - T.Delta_r S^@` से कर सकते है तथा अभिक्रिया के लिए तापमान के साथ `Delta_r H^@` तथा `Delta_r S^@` के मान में परिवर्तन को निम्न प्रकार परिकलित किया जा सकता है
`Delta_r H_(T_2)^@ - Delta_r H_(T_1)^@ = Delta_r C_p^@ (T_2 -T_1)`
` Delta_r S_(T_1)^@ - Delta_r S_(T_1)^@ = Delta_r C_p^@ ln(T_2/T_1)`
`Delta_r G^@ = Delta_r H^@ - T Delta_r S^@`
`Delta_r G^@ =-RT ln K_(eq)` द्वारा
निम्न अभिक्रिया पर विचार करें
`CO(g) +2H_2(g) iff CH_3OH(g)`
दिया है :`Delta_f H^@ (CO, g) = -114`kJ/mole
`S^@ (CH_3OH, g) = 240 "J/K mol" , C_(p,m)^@(H_2,g) = 29JK^(-1) "mol"^(-1)`
`S^@ (CO,g) = 198 "J/mol" -K , C_(p,m)^@ (H_2) = 28.8 ` J/mole - K
`C_(p,m)^@ (CO) = 29.4 `J/mol - K , `C_(p,m)^@ (CH_3OH) = 44 `J/mol-K
तथा `ln (320/300) = 0.06 ` , सभी आँकड़े 300K पर है।
320K ताप पर `Delta_r H^@` है
View Solutionनिश्चित ताप पर अभिक्रिया की मानक गिब्स ऊर्जा `(Delta_r G^@)` का परिकलन `Delta_r G^@ = Delta_r H^@ - T.Delta_r S^@` से कर सकते है तथा अभिक्रिया के लिए तापमान के साथ `Delta_r H^@` तथा `Delta_r S^@` के मान में परिवर्तन को निम्न प्रकार परिकलित किया जा सकता है
`Delta_r H_(T_2)^@ - Delta_r H_(T_1)^@ = Delta_r C_p^@ (T_2 -T_1)`
` Delta_r S_(T_1)^@ - Delta_r S_(T_1)^@ = Delta_r C_p^@ ln(T_2/T_1)`
`Delta_r G^@ = Delta_r H^@ - T Delta_r S^@`
`Delta_r G^@ =-RT ln K_(eq)` द्वारा
निम्न अभिक्रिया पर विचार करें
`CO(g) +2H_2(g) iff CH_3OH(g)`
दिया है :`Delta_f H^@ (CO, g) = -114`kJ/mole
`S^@ (CH_3OH, g) = 240 "J/K mol" , C_(p,m)^@(H_2,g) = 29JK^(-1) "mol"^(-1)`
`S^@ (CO,g) = 198 "J/mol" -K , C_(p,m)^@ (H_2) = 28.8 ` J/mole - K
`C_(p,m)^@ (CO) = 29.4 `J/mol - K , `C_(p,m)^@ (CH_3OH) = 44 `J/mol-K
तथा `ln (320/300) = 0.06 ` , सभी आँकड़े 300K पर है।
320K ताप पर `Delta_r S^@` है
View Solutionनिश्चित ताप पर अभिक्रिया की मानक गिब्स ऊर्जा `(Delta_r G^@)` का परिकलन `Delta_r G^@ = Delta_r H^@ - T.Delta_r S^@` से कर सकते है तथा अभिक्रिया के लिए तापमान के साथ `Delta_r H^@` तथा `Delta_r S^@` के मान में परिवर्तन को निम्न प्रकार परिकलित किया जा सकता है
`Delta_r H_(T_2)^@ - Delta_r H_(T_1)^@ = Delta_r C_p^@ (T_2 -T_1)`
` Delta_r S_(T_1)^@ - Delta_r S_(T_1)^@ = Delta_r C_p^@ ln(T_2/T_1)`
`Delta_r G^@ = Delta_r H^@ - T Delta_r S^@`
`Delta_r G^@ =-RT ln K_(eq)` द्वारा
निम्न अभिक्रिया पर विचार करें
`CO(g) +2H_2(g) iff CH_3OH(g)`
दिया है :`Delta_f H^@ (CO, g) = -114`kJ/mole
`S^@ (CH_3OH, g) = 240 "J/K mol" , C_(p,m)^@(H_2,g) = 29JK^(-1) "mol"^(-1)`
`S^@ (CO,g) = 198 "J/mol" -K , C_(p,m)^@ (H_2) = 28.8 ` J/mole - K
`C_(p,m)^@ (CO) = 29.4 `J/mol - K , `C_(p,m)^@ (CH_3OH) = 44 `J/mol-K
तथा `ln (320/300) = 0.06 ` , सभी आँकड़े 300K पर है।
320K ताप पर `Delta_r H^@` है
View Solutionनिश्चित ताप पर अभिक्रिया की मानक गिब्स ऊर्जा `(Delta_r G^@)` का परिकलन `Delta_r G^@ = Delta_r H^@ - T.Delta_r S^@` से कर सकते है तथा अभिक्रिया के लिए तापमान के साथ `Delta_r H^@` तथा `Delta_r S^@` के मान में परिवर्तन को निम्न प्रकार परिकलित किया जा सकता है
`Delta_r H_(T_2)^@ - Delta_r H_(T_1)^@ = Delta_r C_p^@ (T_2 -T_1)`
` Delta_r S_(T_1)^@ - Delta_r S_(T_1)^@ = Delta_r C_p^@ ln(T_2/T_1)`
`Delta_r G^@ = Delta_r H^@ - T Delta_r S^@`
`Delta_r G^@ =-RT ln K_(eq)` द्वारा
निम्न अभिक्रिया पर विचार करें
`CO(g) +2H_2(g) iff CH_3OH(g)`
दिया है :`Delta_f H^@ (CO, g) = -114`kJ/mole
`S^@ (CH_3OH, g) = 240 "J/K mol" , C_(p,m)^@(H_2,g) = 29JK^(-1) "mol"^(-1)`
`S^@ (CO,g) = 198 "J/mol" -K , C_(p,m)^@ (H_2) = 28.8 ` J/mole - K
`C_(p,m)^@ (CO) = 29.4 `J/mol - K , `C_(p,m)^@ (CH_3OH) = 44 `J/mol-K
तथा `ln (320/300) = 0.06 ` , सभी आँकड़े 300K पर है।
300K ताप पर अभिक्रिया के लिए `Delta_r S^@` है
View Solutionएक गैस के निश्चित द्रव्यमान m की अवस्था परिवर्तन K से L से M से N तथा वापस K में चित्र द्वारा दिखाई गई है।
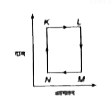
क्रमित परिचालन जो इन अवस्था परिवर्तनों में सहायक है , वह है
View Solutionएक गैस के निश्चित द्रव्यमान m की अवस्था परिवर्तन K से L से M से N तथा वापस K में चित्र द्वारा दिखाई गई है।
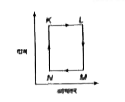
अवस्था परिवर्तनों की स्थितियों में समआयतनिक प्रक्रम युग्म है
View Solution298K पर गैसीय `X_2` का गैसीय X में ऊष्मा अपघटन निम्नलिखित समीकरण
`X_2 (g) iff 2X(g)`
के अनुसार होता है। इस अभिक्रिया की मानक अभिक्रिया गिब्स ऊर्जा `Delta_r G^@` धनात्मक है। अभिक्रिया के प्रारम्भ में `X_2` का 1 मोल है तथा X नहीं है। जैसे-जैसे यह अभिक्रिया बढ़ती है, निर्मित X के मोलों की संख्या `beta` द्वारा दी जाती है। इस प्रकार, साम्यावस्था पर निर्मित X के मोलों की संख्या `beta_("साम्यावरण्या")` है। अभिक्रिया 2 बार के स्थिर कुल दाब पर की जाती है। मान लें कि गैसें आदर्श व्यवहार करती हैं
298 K पर इस अभिक्रिया का `beta_("साम्यावस्था")` के पद में साम्यवस्था स्थिरांक `K_p` क्या होगा
View Solution298K पर गैसीय `X_2` का गैसीय X में ऊष्मा अपघटन निम्नलिखित समीकरण
`X_2 (g) iff 2X(g)`
के अनुसार होता है। इस अभिक्रिया की मानक अभिक्रिया गिब्स ऊर्जा `Delta_r G^@` धनात्मक है। अभिक्रिया के प्रारम्भ में `X_2` का 1 मोल है तथा X नहीं है। जैसे-जैसे यह अभिक्रिया बढ़ती है, निर्मित X के मोलों की संख्या `beta` द्वारा दी जाती है। इस प्रकार, साम्यावस्था पर निर्मित X के मोलों की संख्या `beta_("साम्यावरण्या")` है। अभिक्रिया 2 बार के स्थिर कुल दाब पर की जाती है। मान लें कि गैसें आदर्श व्यवहार करती हैं
298 K पर इस अभिक्रिया का `beta_("साम्यावस्था")` के पद में साम्यवस्था स्थिरांक `K_p` क्या होगा
View Solution
JEE ADVANCED (COMPREHENSION TYPE QUESTIONS) questions and complete solutions for chapter उष्मागतिकी तथा उष्मारसायन of ERRORLESS CHEMISTRY (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 CHEMISTRY उष्मागतिकी तथा उष्मारसायन
- ASSERTION AND REASON
- CRITICAL THINKING
- JEE ADVANCED (COMPREHENSION TYPE QUESTIONS)
- JEE ADVANCED (INTEGER TYPE QUESTIONS)
- JEE ADVANCED (MATRIX MATCH TYPE QUESTIONS)
- JEE ADVANCED (MORE THAN ONE CORRECT ANSWERS)
- JEE ADVANCED (REASONING TYPE QUESTIONS)
- MULTIPLE CHOICE QUESTIONS ( अभिक्रिया की ऊष्मा)
- MULTIPLE CHOICE QUESTIONS ( ऊष्मागतिकी का द्वितीय और तृतीय नियम तथा एण्ट्रॉपी)
- MULTIPLE CHOICE QUESTIONS ( ऊष्मागतिकी का प्रथम नियम तथा हैस का नियम)
- MULTIPLE CHOICE QUESTIONS ( बंध ऊर्जा)
- MULTIPLE CHOICE QUESTIONS ( मुक्त ऊर्जा एवं कार्य फलन)
- MULTIPLE CHOICE QUESTIONS (आधारभूत धारणा)