Complete Solutions to Exercise of chapter केन्द्रीय प्रवृत्ति के माप of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | केन्द्रीय प्रवृत्ति के माप |
| ERRORLESS HINDI | Exercise |
| Number Of Questions | 54 |
| Academic Year | 2023-24 |
एक कक्षा में लड़कों का औसत अंक 52 है तथा लड़कियों का औसत अंक 42 है। लड़के तथा लड़कियों का संयुक्त (combined) औसत अंक 50 है। कक्षा में लड़कों का प्रतिशत है
View Solutionकिसी समूह की 50 संख्याओं का समान्तर माध्य 38 है यदि समूह की दो संख्यायें 55 तथा 45 हटा दी जायें, तब शेष संख्याओं के समूह का समान्तर माध्य है
View Solutionकिसी कक्षा के 35 छात्रों का औसत भार 40 किग्रा है। यदि इसमें शिक्षक का भार शामिल किया जाये, तब औसत `1/2` किग्रा बढ़ जाता है, शिक्षक का भार है
View Solution100 छात्रों की एक कक्षा में 70 लड़के है, जिनके किसी विषय में औसत अंक 75 है। यदि सम्पूर्ण कक्षा के औसत अंक 72 है, तब लड़कियों के औसत अंक हैं
View Solutionयदि समूह की संख्याओं `x_1,x_2,x_3`,….`x_n` का माध्य `barx` हैं, तब संख्याओं `x_i+2i,1 le I le n` का माध्य है
View Solution100 पदों का माध्य 49 है। बाद में यह पाया गया, कि तीन पद जो कि 60, 70, 80 होना चाहियें, गलती से क्रमशः 40, 20, 50 पढ़े गये थे। सही माध्य है
View Solutionएक विद्यालय की कक्षा XII में रसायन के 4 विभाग हैं जिनमें 40, 35, 45 तथा 42 छात्र हैं। इन चार विभागों द्वारा रसायन के प्रश्न-पत्र में प्राप्त माध्य अंक क्रमशः 50, 60, 55 तथा 45 हैं, तब सभी विभागों का प्रति विद्यार्थी अंको का औसत है
View Solutiona से शुरू होते हुए 7 क्रमागत पूर्णांकों का समान्तर माध्य m है। तब a+ 2 से शुरू होने वाले 11 क्रमागत पूर्णांकों का समान्तर माध्य हैं
View Solution9 पदों का समान्तर माध्य 15 है। यदि इस श्रेणी में एक ओर पद जोड़ दिया जाए, तब समान्तर माध्य 16 हो जाता है। तब जोड़े गए पद का मान है
View Solutionदुर्बल विषमीय बंटन के माध्य, माध्यिका तथा बहुलक के मध्य सम्बन्ध है
View Solutionयदि प्रसरण v तथा मानक विचलन `sigma` है, तब
View Solutionयदि आँकड़ों का प्रत्येक प्रेक्षण, जिसका प्रसरण `sigma^2` है, `lambda` से बढ़ाया जाता है, तब नये समूह का प्रसरण है
View Solutionकिसी सामान्य वक्र (Normal curve) के लिये महत्तम कोटि है
View Solutionमाना एक जनसंख्या A के लिए 100 प्रेक्षण 101, 102,...., 200 तथा अन्य जनसंख्या B के लिए 100 प्रेक्षण 151, 152, ..... 250 है। यदि `V_A` तथा `V_B` क्रमशः दो जनसंख्याओं के प्रसरण को प्रदर्शित करते है तब `V_A/V_B` है
View Solutionकिसी समूह के प्रेक्षणों - 1, 0, 4 के लिये माध्य से माध्य विचलन है
View Solution15 पदों का मानक विचलन 6 है। यदि प्रत्येक पद से 1 घटा दिया जाये, तब मानक विचलन होगा
View Solution10 अवलोकनों का उनके माध्य 50 से विचलनों के वर्गों का योगफल है 250 तो विचरण गुणांक है :
View Solutionपाँच प्रेक्षणों का माध्य 4 है तथा इनका प्रसरण 5.2 है। यदि इन प्रेक्षणों में से तीन 1, 2 तथा 6 है, तब अन्य दो प्रेक्षण हैं
View Solutionकिसी समूह के प्रेक्षणों `x_1,x_2,x_3`,….,`x_101` पर विचार करते हैं। यह दिया गया है, कि `x_1 lt x_2 lt x_3lt` ….`ltx_100 lt x_101` , तब इस समूह के प्रेक्षणों का एक बिन्दु k के परितः माध्य विचलन न्यूनतम होगा जबकि k का मान है
View Solution(2n+1) प्रेक्षणों `x_1-x_1,x_2-x_2`,…..`x_n ,-x_n` तथा 0 (शून्य) के लिये (जहाँ x के सभी मान भिन्न है)। माना S.D तथा M.D. क्रमशः मानक विचलन तथा माध्यिका प्रदर्शित करते हैं, तब निम्न में से कौनसा सदैव सत्य है
View Solutionमाना एक चर x द्वारा लिये गये मान इस प्रकार हैं, कि `ale x_i le b` जहाँ `x_i`, 1 = 1,2. ....n के लिये iवी स्थिति में x का मान प्रदर्शित करता है
View Solutionनिम्नलिखित श्रेणी का मानक विचलन है।

View Solutionकिसी प्रयोग में x पर 15 प्रेक्षणों के निम्न परिणाम प्राप्त होते हैं, `sum x^2=2830 , sumx=170` प्रेक्षण करने पर एक मान 20 गलत पाया गया तथा उसे सही मान 30 से प्रतिस्थापित किया गया तब सही प्रसरण है
View Solution7 व्यक्तियों के दैनिक वेतन (रुपयों में) निम्न है 12, 7, 15 10, 17, 19, 25, तब दैनिक वेतन का चतुर्थक विचलन है
View Solutionयदि चर 0, 1, 2, ..... n मान ग्रहण करता है. जबकि बारम्बारताऐं क्रमशः द्विपद गुणांकों C(n, 0), C(n, 1), C(n, 2), ...., C(n, n) के समानुपाती हैं, तब बंटन का प्रसरण है
View Solutionदो आँकड़ा-समुच्चय, जिनमें से प्रत्येक में 5 अवयव है, के प्रसरण 4 तथा 5 हैं तथा उनके तदनुरूपी माध्य क्रमशः 2 तथा 4 हैं। मिश्रित औंकड़ा-समुच्चय का प्रसरण हैं
View Solutionn पदों का माध्य `barx` है। यदि प्रथम पद को 1, द्वितीय पद को 2 तथा इसी प्रकार आगे के पदों को बढ़ाया जाये तब नया माध्य होगा
View Solutionमानों 0, 1, 2, 3,..., n जिनके संगत भार क्रमश: `n_(C_0),n_(C_1),...,n_(C_n)` हैं, का माध्य है
View Solution100 प्रेक्षणों का माध्य 45 है। बाद में यह पाया गया कि दो प्रेक्षण 19 तथा 31 गलती से 91 तथा 13 लिये गये थे सही माध्य है
View Solutionn संख्याओं `x_1,x_2,x_3`,…..`x_n` का औसत M है। यदि `x_n` को x' से बदल दिया जाये तब नया औसत होगा
View Solutionछात्रों की ऊँचाईयों के बंटन के आंकड़े निम्नानुसार हैं।
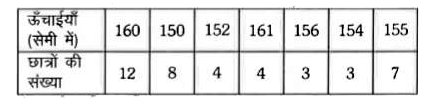
बंटन की माध्यिका हैं।
View Solution200 उम्मीदवारों के अंकों का माध्य तथा मानक विचलन क्रमशः 40 तथा 15 है। बाद में, यह पाया गया कि किसी संख्या 40 को गलती से 50 पढ़ा गया है सही माध्य तथा मानक विचलन क्रमशः हैं
View Solutionकिसी समूह के प्रेक्षणों `x_1,x_2`,…`x_n` के लिये परिसर r तथा मानक विचलन `S^2=1/(n-1)sum_(i=1)^n (x_i-barx)^2` हैं, तब
View Solution2n प्रेक्षणों की एक श्रेणी में, आधे a के बराबर तथा शेष आधे -a के बराबर हैं। यदि प्रेक्षणों का मानक विचलन 2 है, तब |a|=
View Solutionकिसी चर x का मानक विचलन `sigma` है । तब चर `(ax+b)/c` का मानक विचलन है, (जहाँ a, b, c अचर है)
View Solutionयदि संख्याओं 1, 1+ d, 1+ 2d, .....1+ 100d का उनके माध्य से माध्य विचलन 255 है, तब d बराबर है।
View Solutionसंख्याओं a, b, 8, 5, 10 का माध्य 6 है तथा प्रसरण 6.80 है। तो निम्न में से कौन-सा एक विकल्प a तथा b के सम्भावित मान देगा
View Solutionयदि संख्याओं 1, 2, 3, ....98, 99, x का औसत 100x है, तब x का मान है
View Solutionn प्रेक्षणों `x_1,x_2,x_3`...., `x_n` का माध्य तथा प्रसरण क्रमशः 5 तथा 0 हैं। यदि `sum_(i=1)^(n) x_i^2 = 400`, तब n का मान है
View Solutionदो बंटनों के प्रसरण गुणांक 55 तथा 65 हैं एवं उनके मानक विचलन क्रमशः 22 तथा 39 हैं, तब उनके समान्तर माध्य क्रमशः हैं
View Solutionप्रथम 20 प्राकृत संख्याओं का प्रसरण है
View Solutionयदि दो समूहों का यौगिक माध्य `40/3` है तथा एक समूह का माध्य 15 है जिसमें 10 अवलोकन है, तो अन्य समूह का माध्य ज्ञात कीजिए जिसमें 8 अवलोकन है।
View Solutionपाँच अवलोकनों का माध्य 4 है तथा उनका प्रसरण 5.2 है । यदि उनमें से तीन अवलोकन 2, 4 तथा 6 है तब अन्य दो अवलोकन है
View Solutionएक कक्षा में, गणित की परीक्षा में 10 विद्यार्थियों में से प्रत्येक 100 अंक प्राप्त करता है, 2 विद्यार्थी शून्य अंक पाते है तथा बचे हुए विद्यार्थियों में औसत विद्यार्थी 72 अंक पाते हैं। यदि कक्षा का औसत 76 है, तो कक्षा में विद्यार्थियों की संख्या है
View Solutionपुरूषों तथा महिलाओं के एक संयुक्त समूह की माध्य आयु 25 वर्ष है यदि पुरूषों के समूह की माध्य आयु 26 तथा महिलाओं के समूह की 21 है, तब समूह में पुरूषों तथा महिलाओं का प्रतिशत होगा
View Solutionएक कार यात्रा का प्रथम आधा भाग `v_1` वेग से तथा शेष आधा भाग `v_2` वेग से पूर्ण करती है। सम्पूर्ण यात्रा के लिये कार की औसत चाल है
View Solutionयदि एक चर 0,1,2,…,n मान ग्रहण करता है, जबकि आवृत्तियों `q^n , n/1 q^(n-1) p, (n(n-1))/1.2 q^(n-2) p^2`, …., `p^n` हैं, जहाँ p+q= 1, तब माध्य है
View Solutionनिम्नलिखित सारणी से माध्यिका का मान है
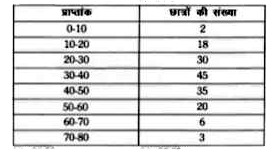
View Solutionप्रथम n प्राकृत संख्याओं का मानक विचलन (S.D.) है
View Solutionएक समूह की पाँच संख्याओं का माध्य 8 तथा प्रसरण 18 है तथा दूसरे समूह की 3 संख्याओं का माध्य 8 तथा प्रसरण 24 है। तब संख्याओं के संयुक्त समूह का प्रसरण है
View Solutionयदि 1, 2, 3, 4, 5, ....... 10 का प्रसरण `99/12` है, तब 3, 6, 9, 12,….,30 का मानक विचलन है
View Solutionकिसी असतत् श्रेणी में (जबकि सभी मान समान नहीं हैं) माध्य से माध्य विचलन तथा मानक विचलन के मध्य सम्बन्ध है
View Solutionयदि बंटन `(y_i,f_i)` का माध्य `mu` है, तथा `sum f_i (y_i - mu)`=
View Solutionयदि `x_1,x_2`,….`x_18` प्रेक्षण इस प्रकार हैं कि `sum_(j=1)^(18) (x_j-8)=9` तथा `sum_(j=1)^18 (x_j-8)^2=45`, तब इन प्रेक्षणों का मानक विचलन है
View Solution
Exercise questions and complete solutions for chapter केन्द्रीय प्रवृत्ति के माप of ERRORLESS MATHS (HINDI) of Class 12