Complete Solutions to JEE Advanced (More than one correct answers) of chapter सदिश बीजगणित of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | सदिश बीजगणित |
| ERRORLESS HINDI | JEE Advanced (More than one correct answers) |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
वह सदिश जो सदिशों `hati+hatj+2hatk` तथा`hati+2hatj+hatk` के समतलीय है और सदिश `hati+hatj+hatk` के लम्बवत है होंगें
View Solutionमाना `vec(A)`, मुलबिन्दु से गुजरने वाले समतल `P_(1)` और `P_(2)` की प्रतिच्छेद की रेखा के समान्तर सदिश है | समतल `P_(1)`, सदिश `2hatj+3hatk` और `4hatj-3hatk` के समान्तर है तथा समतल `P_(2),hatj-hatk` और `3hati+3hatj` के समान्तर है, तब सदिश `vec(A)` और `2hati+hatj-2hatk` के बीच का कोण है
View Solutionमाना कि a और b दो एकक असंरेख सदिश हैं | यदि `u=a-(a.b)b` और `v=axxb` हों, तो `|v|=`
View Solutionनिम्नलिखित व्यंजकों में से कौनसे अर्थपूर्ण हैं
View Solutionसदिश `(1)/(3)(2i-2j+k)` है
View Solutionमाना `a=2i-j+k,b=i+2j-k` व `c=i+j-2k` तीन सदिश हैं | तब सदिश b व c के तल में वह सदिश, जिसका a पर प्रक्षेप का परिमाण `sqrt((2)/(3))` है, है
View Solutionयदि सरल रेखाएँ `(x-1)/(2)=(y+1)/(k)=z/2` और `(x+1)/(5) = (y+1)/(2)=z/k` समतलीय हैं, तो वह (वे) समतल, जिसमें ये दोनों रेखाएँ स्थित हैं, निम्न है/हैं
View Solutionएक सदिश `hati+x hatj+3hatk` परिमाण में दुगना है तथा कोण `theta` के परित: घूर्णन करके `4hati+(4x-2)hatj+2hatk` हो जाता है, तब x का मान है
View Solutionयदि तीन सदिश `vec(a),vec(b)` तथा `vec(c)` समतलीय इकाई सदिश इस प्रकार हो कि `vec(a)+vec(b)+vec(c)=0` यदि तीन सदिश `vec(p),vec(q)` तथा `vec(r)` क्रमश: `vec(a),vec(b)` तथा `vec(c)`, के समान्तर हो तथा अलग-अलग परिमाण के पूर्णत: है, तब निम्न चुनावों के बीच, `|vec(p)+vec(q)+vec(r)|` का मान बराबर है
View Solutionचतुर्थ विमीय में, अक्षों के अनुदिश इकाई सदिश `hati,hatj,hatk` तथा `hatl` है तथा `vec(a)_(1),vec(a)_(2),vec(a)_(3),vec(a)_(4)` चार अशून्य सदिश इस प्रकार है कि कोई भी सदिश दूसरों सदिशों के रेखीय युग्म को प्रदर्शित नहीं करता है तथा `(lambda-1)(vec(a)_(1)-vec(a)_(2))+mu(vec(a)_(2)+vec(a)_(3))+gamma`
`(vec(a)_(3)+vec(a)_(4)-2vec(a)_(2))+vec(a)_(3)+delta vec(a)_(4)=vec(0)`, तब
View Solution`vec(b)` तथा `vec(c)` असंरेखीय सदिश है यदि `vec(a)xx(vec(b)xxvec(c))+(vec(a).vec(b))vec(b)=(4-2x-siny)vec(b)+(x^(2)-1)vec(c)` तथा `(vec(c).vec(c))vec(a)=vec(c)` है, तब
View Solutionएक समान्तर चतुर्भुज बनाया जाता है जिसकी दो आसन्न भुजाऐं `vec(a)` तथा `vec(b)` है एक सदिश जो समान्तर चतुर्भुज का शीर्षलम्ब तथा `vec(a)` पर लम्ब हो, है
View Solutionयदि सदिशों `vec(b)=(tan alpha,-1,2sqrt(sin alpha//2))` तथा `vec(c)=(tan alpha, tan alpha,-(3)/(sqrt(sin alpha//2)))` अभिलम्बवत है तथा सदिश `vec(a)=(1,3,sin2alpha)`, z-अक्ष के साथ न्यूनकोण बनाती हो, तो `alpha` का मान है
View Solution`vec(A)` तथा `vec(B)` सदिश समीकरणों `vec(A)+vec(B)=vec(a),vec(A)xxvec(B)=vec(b)` तथा `vec(A).vec(a)=1`, को सन्तुष्ट करतें हैं जहाँ `vec(a)` तथा `vec(b)` दिए गए सदिश है, वे हैं.
View Solutionएक त्रिभुज के कोण हैं, जिसकी दो भुजाओं को सदिशों `sqrt(3)(hata xx hatb)` तथा `hatb-(hata.hatb)hata` के द्वारा प्रदर्शित किया जाता है | जहाँ `vec(b)` एक अशून्य सदिश तथा `hata,vec(a)` की दिशा में इकाई सदिश है
View Solutionदो अदिश इस प्रकार है कि `l vec(a)+m vec(b)=vec(c)`, जहाँ `vec(a),vec(b)` तथा `vec(c)` दिए गए सदिश हैं, बराबर है
View SolutionA, B, C तथा D चार बिंदु इस प्रकार है कि
`vec(AB)=m(2hati-6hatj+2hatk),vec(BC)=(hati-2hatj)` तथा `vec(CD)=n(-6hati+15hatj-3hatk)` यदि कुछ बिन्दु E पर CD, AB को प्रतिच्छेद करता है, तब
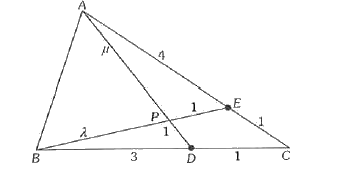
View Solution`DeltaABC` में D तथा E क्रमश: BC तथा AC पर बिन्दु इस प्रकार हैं कि `BD=3DC` तथा `AE=4EC` रेखाओं AD तथा BE बिन्दु P पर प्रतिछेद करती है तब
View Solutionत्रिभुज `DeltaABC` में, माना I तथा O क्रमानुसार अंत: केन्द्र तथा वृत्त केन्द्र हो, तो
View Solutionमाना `vec(b)=4vec(i)+3vec(j)`, यदि सदिश `vec(c)`, सदिश `vec(b)` पर लम्ब हो तथा xy समतल में स्थित हो, एक सदिश xy समतल में `vec(b)` तथा `vec(c)` के अनुदिश प्रक्षेप क्रमश: 1 तथा 2 है, तब सदिश है
View Solutionमाना की सदिशों (vectors) `vec(x),vec(y)` तथा `vec(z)` में प्रत्येक का परिमाण `sqrt(2)` हैं तथा प्रत्येक युग्म के मध्य का कोण `(pi)/(3)` है | यदि शून्येतर (non-zero) सदिश `vec(a)` सदिशों `vec(x)` तथा `vec(y)xx vec(z)`, के लम्बवत है, तब
View Solutionमाना कि `DeltaPQR` एक त्रिभुज है | माना कि `vec(a)=vec(QR),vec(b)=vec(RP)` और `vec(c)=vec(PQ)` है | यदि `|vec(a)|=12,|vec(b)|=4sqrt(3)` और `vec(b).vec(c)=24`, तब निम्नलिखित में से कौन सा (से) सही है (हैं)
View Solutionविचार कीजिये, एक सूच्याकार (pyramid, OPQRS) जो प्रथम अष्टांशक (first octant) `(x ge 0,y ge0,z ge0)` में स्थित है, जिसमें O मुलबिन्दु (origin) तथा OP तथा OR क्रमश: x- अक्ष है | इस सूच्याकार का आधार (base) OPQR एक वर्ग (square) है जिसमें OP = 3 है | बिन्दु S कर्ण (diagonal) OQ के मध्यबिन्दु T के ठीक ऊपर इस प्रकार है कि `TS=3` है, तब
View Solutionमाना कि `R^(3)` में `vecu=u_(1)hati+u_(2)hatj+u_(3)hatk` एक मात्रक सदिश (unit vector) है और `vecw=(1)/(sqrt(6))(hati+hatj+2hatk)` है | दिया हुआ है कि `R^(3)` में सदिश `vec(v)` का अस्तित्व इस प्रकार है कि `|vecu xx vec(v)|=1` और `vecw.(vecu xx vec(v))=1` है | निम्नलिखित में से कौन सा कथन सहीं है
View Solutionमाना कि O मुलबिन्दु है एवं PQR एक स्वेच्छिक त्रिभुज है | बिन्दु S इस प्रकार है कि
`vec(OP).vec(OQ)+vec(OR).vec(OS)=vec(OR).vec(OP)+vec(OQ).vec(OS)=vec(OQ).vec(OR)+vec(OP).vec(OS)`
तब बिन्दु S त्रिभुज PQR का है
View Solution
JEE Advanced (More than one correct answers) questions and complete solutions for chapter सदिश बीजगणित of ERRORLESS MATHS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 MATHS सदिश बीजगणित
- Exercise
- ILLUSTRATION
- JEE Advanced (Comprehension type questions) Passage - I
- JEE Advanced (Comprehension type questions) Passage - II
- JEE Advanced (Comprehension type questions) Passage - III
- JEE Advanced (Comprehension type questions) Passage - IV
- JEE Advanced (Comprehension type questions) Passage - V
- JEE Advanced (Comprehension type questions) Passage - VI
- JEE Advanced (Comprehension type questions) Passage - VII
- JEE Advanced (Comprehension type questions) Passage - VIII
- JEE Advanced (Integer type questions)
- JEE Advanced (Matrix Match type questions)
- JEE Advanced (More than one correct answers)
- JEE Advanced (Reasoning type questions)
- Solved Multiple Choice Questions (अदिश त्रिगुणन तथा उसके अनुप्रयोग)
- Solved Multiple Choice Questions (त्रिविमीय ज्यामिति में सदिशों का अनुप्रयोग)
- Solved Multiple Choice Questions (दो सदिशों का अदिश गुणन तथा उसके अनुप्रयोग)
- Solved Multiple Choice Questions (सदिश का मापांक, सदिशों का बीजगणित)
- Solved Multiple Choice Questions (सदिश त्रिगुणन)