Complete Solutions to ILLUSTRATION of chapter अवकलन तथा अवकलज के अनुप्रयोग of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | अवकलन तथा अवकलज के अनुप्रयोग |
| ERRORLESS HINDI | ILLUSTRATION |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
If `y=t^(4//3)-3t^(-2//3)`, then `dy//dt=`
View SolutionDerivative of `tanx-x` w.r.t to `x` is :
View Solutionयदि `y=2^(logx)`, तब `(dy)/(dx)` है
View Solution`(d)/(dx)(e^(x^(3)))` का मान है
View Solution`(d)/(dx)[log(x-(1)/(x))]=`
View Solutionयदि `x=a(t-sint)` तथा `y=a(1-cost)`, तो `(dy)/(dx)=`
View Solutionयदि `tany=(2t)/(1-t^(2))` तथा `sinx=(2t)/(1+t^(2))`, तो `((dy)/dx)=`
View Solutionयदि `x=at^(2),y=2at`, तब `(d^(2)y)/(dx^(2))`=
View Solutionयदि `x=2cost-cos2t,y=2sint-sin2t` , तो `t=(pi)/(4)` पर `(dy)/(dx)=`
View Solutionयदि `y=e^(x)logx`, तब `(dy/dx)` है
View Solution`(d)/(dx)(x^(2)e^(x)sinx)=`
View Solution`(d)/(dx)((1)/(x^(4)secx))=`
View Solutionयदि `cos(x+y)=ysinx`, तो `(dy)/(dx)`=
View Solutionयदि `x^(3)+8xy+y^(3)=64`, तो `(dy)/(dx)=`
View Solutionयदि `3sin(xy)+4cos(xy)=5`, तो `(dy)/(dx)`=
View Solution`(d)/(dx){(sinx)^(logx)}=`
View Solution`(d)/(dx)(x^(log_(e)^(x)))=`
View Solutionयदि `y=sqrt(((x-a)(x-b))/((x-c)(x-d)))`, तो `(dy)/(dx)`=
View Solutionयदि `x=a(tcost-sint),y=a(tsint+cost)`, तो `(dy)/(dx)` बराबर है
View Solutionयदि `x=sintcos2t` और `y=costsin2t`, तब `t=(pi)/(4)`पर `(dy)/(dx)`=
View Solutionयदि `y=sqrt(sinx+sqrt(sinx+sqrt(sinx+...oo)))` तब
View Solutionयदि `y=sqrt(x+sqrt(x+sqrt(x+........oo)))` तब `(dy)/(dx)=`
View Solutionयदि `y=(sinx)^((sinx)^(sinx.....oo))` , तो `(dy)/(dx)`=
View Solutionयदि `x=e^(y+e^(y+...oo)),xgt0`, तब `(dy)/(dx)` है
View Solutionयदि
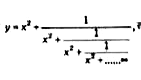 तो `(dy)/(dx)=`
तो `(dy)/(dx)=`
View Solution`cos^(-1)(sqrt(x))` का `sqrt((1-x))` के सापेक्ष अवकल गुणांक है
View Solution`cos^(-1)sqrt(1-x^(2))` के सापेक्ष `sin^(-1)x` का अवकलन गुणांक है
View Solution`tan^(-1)x` के सापेक्ष `tan^(-1)((sqrt(1+x^(2))-1)/(x))` का अवकलन गुणांक है
View Solution`tan^(-1)sqrt(x)` का `sqrt(x)` के सापेक्ष अवकलन गुणांक है
View Solutionयदि `y=Acosnx+Bsinnx`, तो `(d^(2)y)/(dx^(2))` =
View Solutionयदि `y="cos"^(2)(3x)/(2)-"sin"^(2)(3x)/(2)`, तब `(d^(2)y)/(dx^(2))` है
View Solutionयदि `y=x^(2)e^(mx)`, जहाँ m अचर है , तो `(d^(3)y)/(dx^(3))`=
View Solution`(d^(n))/(dx^(n))(logx)`=
View Solution`cos^(2)x` का n वाँ अवकलन =
View Solutionयदि `z=tan^(-1)((x)/(y))`, तो `z_(x):z_(y)=`
View Solutionयदि `u=(x+y)/(x-y)`, तो `(varthetau)/(varthetax)+(varthetau)/(varthetay)`=
View Solutionयदि `u=sin^(-1)((y)/(x))`, तो `(varthetau)/(varthetax)`=
View Solutionयदि `z=((x^(4)+y^(4))^(1//3))/((x^(3)+y^(3))^(1//4))`, तो `x(varthetaz)/(varthetax)+y(varthetaz)/(varthetay)`=
View Solutionयदि `u="tan"^(-1)(y)/(x)`, तो यूलर प्रमेय द्वारा `x(varthetau)/(varthetax)+y(varthetau)/(varthetay)`=
View Solutionयदि `z=sec^(-1)((x^(4)+y^(4)-8x^(2)y^(2))/(x^(2)+y^(2)))` तब `x(varthetaz)/(varthetax)+y(varthetaz)/(varthetay)` बराबर है
View Solutionयदि `F(u)=f(x,y,z),x,y,z` में n घाट का समघातीय फलन हो , तब `x(varthetau)/(varthetax)+y(varthetau)/(varthetay)+z(varthetau)/(varthetaz)`=
View Solutionरेखा में गतिमान एक कण की गति का समीकरण `v^(2)=2-3x` है। यदि रेखा के एक निश्चित बिंदु से `x` मापा गया हो ,तो कण का त्वरण होगा
View Solutionस्वतंत्रतापूर्वक गिरता हुआ एक पत्थर `t` सेकण्ड में `s` दूरी तय करता है , जहाँ `s=(1)/(2)g t^(2)` , तब पत्थर का त्वरण है
View Solutionएक कण एक सरल रेखा में इस प्रकार चलता है कि t सेकण्ड में वह `at^(3)+bt+5` मीटर दूरी तय करता है। यदि उसका त्वरण 4 सेकण्ड के पश्चात `48`मीटर /सेकण्ड`"^(2)` हो ,तो a बराबर है
View Solutionउर्ध्वाधरतः ऊपर कि ओर गतिमान एक पत्थर कि गति का समीकरण `s=490t-4.90t^(2)` है ,तब पत्थर द्वारा प्राप्त महत्तम ऊँचाई होगी
View Solutionयदि एक गोलाकार गुब्बारे का चर व्यास `3x+(9)/(2)` हो , तो x के सापेक्ष उसके आयतन में परिवर्तन की दर होगी
View Solutionचर घन की एक कोर 10 सेमी /सेकण्ड की दर से बढ़ रही है। जब कोर 5 सेमी लम्बाई की हो , तो कितनी शीघ्रता से घन का आयतन बढ़ेगा
View Solutionधातु की एक वर्गाकार चादर की भुजा की लम्बाई 4सेमी/सेकण्ड की दर बढ़ रही है। जब भुजा की लम्बाई 2 सेमी है , तब उसका क्षेत्रफल किस दर से बढ़ रहा है
View Solutionवक्र `x=t^(2)+3t-8,y=2t^(2)-2t-5` के बिंदु (2,-1) पर स्पर्श रेखा की प्रवणता है
View Solutionवक्र `y^(2)=2(x-3)` का वह बिंदु जिस पर अभिलम्ब रेखा `y-2x+1=0` के समांतर है , है
View Solutionयदि वक्र `y=f(x)` का अभिलम्ब, x- अक्ष के समांतर हो , तो निम्न कथन सत्य है
View Solutionवक्र `y=2cosx` के बिंदु `x=(pi)/(4)` पर स्पर्श रेखा का समीकरण होगा
View Solutionवक्र `y=x^(4)` पर बिंदु (2,0) , जो वक्र पर नहीं है , से स्पर्श रेखा का समीकरण है
View Solutionवक्र `x^(2)=-4y` के बिंदु `(-4,-4)` पर स्पर्श रेखा का समीकरण है
View Solutionयदि `x=t^(2)` और `y=2t`, तब t=1 पर अभिलम्भ का समीकरण होगा
View Solutionवक्र `y^(4)=ax^(3)` के बिंदु (a,a) पर अभिलम्भ का समीकरण है
View Solutionवक्रो `y^(2)=4x+4` एवं `y^(2)=36(9-x)` के बीच का कोण है
View Solutionव्रक्रो `y=sinx` तथा `y=cosx` के मध्य कोण है
View Solutionफलन `(x-1)(x-2)^(2)` का उच्चिष्ठ मान है
View Solutionफलन `|sin4x+3|` के क्रमशः उच्चिष्ठ एवं निम्निष्ठ मान है
View Solutionफलन `(x-1)(x+2)^(2)` के स्थानीय उच्चिष्ठ तथा स्थानीय निम्निष्ठ मान है
View Solutionफलन `(logx)/(x)` का स्थानीय महत्तम मान है
View Solutionफलन `((1)/(x))^(x)` का उच्चिष्ठ मान है
View Solutionयदि दो संख्याओं का योग 3 है , तो प्रथम संख्या का दूसरी संख्या के वर्ग से गुणनफल का उच्चिष्ठ मान है
View Solution`2x+3y` का न्यूनतम मान ,जबकि `xy=6` है , है
View Solutionफलन `x^(3)-18x^(2)+96x` के अंतराल (0,9) में उच्चिष्ठ एवं निम्निष्ठ मान है
View Solutionअंतराल `[1,e]` में `x^(2)logx` का महत्तम मान है
View Solutionअंतराल `[0,2pi]` में बिंदु जहाँ `f(x)=e^(x)sinx` की प्रवणता अधिकतम है , है
View Solutionफलन `f(x)=(4)/(3)x^(3)-8x^(2)+16x+5` के लिए `x=2` एक बिंदु है
View Solutionफलन `x^(4)-4x ` किस अंतराल में ह्यसमान है
View Solutionकिस अंतराल के लिए फलन `f(x)=-2x^(3)-9x^(2)-12x+1` ह्यसमान है
View Solutionफलन `(f(x)=cosx-2px` एकदिष्ट ह्यसमान है
View Solutionनिम्न में से किस अंतराल में फलन `f(x)=x^(3)-3x^(2)-24x+5` वर्धमान फलन है
View Solutionफलन `f(x)=sin2x` के लिए कौन सा कथन सही है
View Solutionकिस अंतराल के लिए फलन `(x^(2)-3x)/(x-1)` रोले प्रमेय की सभी शर्तों को संतुष्ट करता है
View Solution`[-1,1]` पर परिभाषित फलन `f(x)=|x|` के लिए रोले का प्रमेय लागू नहीं है क्योँकि
View Solutionयदि फलन `f(x)=x^(3)-6x^(2)+ax+b` रोले प्रमेय को अंतराल `[1,3]` में संतुष्ट करता है और `f'((2sqrt(3)+1)/(sqrt(3)))=0`, तब
View Solutionअंतराल `-1lexle1` में रोले की प्रमेय किस फलन पर लागू है
View Solutionफलन `f(x)=e^(x),a=0,b=1` के लिए माध्यम प्रमेय में c का मान होगा
View Solutionयदि `f(x)=cosx,0lexle(pi)/(2)` , तब माध्यम प्रमेय में 'c' का वास्तविक मान है
View Solutionमध्यमान प्रमेय `f(b)-f(a)=(b-a)f'(x_(1)),altx_(1)ltb` से यदि `f(x)=(1)/(x)`, तो `x_(1)=`
View Solutionफलन `f(a)=log_(e)x`, मध्यमान प्रमेय की शर्तों को `[1,3]` में संतुष्ट करता है , तो c का मान है
View Solutionयदि मध्यमान प्रमेय का रूप `f(b)-f(a)=(b-a)f'(c )` है , तो फलन `x^(2)-2x+3` के अंतराल `[1,(3)/(2)]` में c का मान है
View Solutionयदि `y=t^(4//3)-3t^(-2//3)`, तो `dy//dt=`
View Solution`tanx-x` का x के सापेक्ष अवकलन गुणांक होगा
View Solutionयदि `y=2^(logx)`, तब `(dy)/(dx)` है
View Solution`(d)/(dx)(e^(x^(3)))` का मान है
View Solution`(d)/(dx)[log(x+(1)/(x))]=`
View Solutionयदि `x=a(t-sint)` तथा `y=a(1-cost)`, तो `(dy)/(dx)=`
View Solutionयदि `tany=(2t)/(1-t^(2))` तथा `sinx=(2t)/(1+t^(2))`, तो `(dy)dx)=`
View Solutionयदि `x=at^(2),y=2at`, तब `(d^(2)y)/(dx^(2))`=
View Solutionयदि `x=2cost-cos2t,y=2sint-sin2t` , तो `t=(pi)/(4)` पर `(dy)/(dx)=`
View Solutionयदि `y=e^(x)logx`, तब `(dy)dx)` है
View Solution`(d)/(dx)(x^(2)e^(x)sinx)=`
View Solution`(d)/(dx)((1)/(x^(4)secx))=`
View Solutionयदि `cos(x+y)=ysinx`, तो `(dy)/(dx)`=
View Solutionयदि `x^(3)+8xy+y^(3)=64`, तो `(dy)/(dx)=`
View Solutionयदि `3sin(xy)+4cos(xy)=5`, तो `(dy)/(dx)`=
View Solution`(d)/(dx){(sinx)^(logx)}=`
View Solution`(d)/(dx)(x^(log_(e)^(x)))=`
View Solution
ILLUSTRATION questions and complete solutions for chapter अवकलन तथा अवकलज के अनुप्रयोग of ERRORLESS MATHS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 MATHS अवकलन तथा अवकलज के अनुप्रयोग
- EXERCISE
- ILLUSTRATION
- JEE Advanced (Comprehension type questions)
- JEE Advanced (Integer type questions)
- JEE Advanced (Matrix Match type questions)
- JEE Advanced (More than oen correct answers)
- JEE Advanced (Reasoning thye questions)
- MULTIPLE CHOICE QUESTIONS (अस्पष्ट फलनों का अवकलन,प्रचलिक व संयुक्त फलनों का अवकलन,लघुगणकीय अवकलन, अनन्त श्रेणियों के अवकलन )
- MULTIPLE CHOICE QUESTIONS (आंशिक अवकलन )
- MULTIPLE CHOICE QUESTIONS (उच्चिष्ठ तथा निम्निष्ठ)
- MULTIPLE CHOICE QUESTIONS (एक बिन्दु पर अवकलज,मानक अवकलज)
- MULTIPLE CHOICE QUESTIONS (यांत्रिकी में अनुप्रयोग व परिवर्तन की दर )
- MULTIPLE CHOICE QUESTIONS (रोले की प्रमेय, लेग्रांज की मध्यमान प्रमेय )
- MULTIPLE CHOICE QUESTIONS (वर्धमान तथा ह्रासमान फलन)
- MULTIPLE CHOICE QUESTIONS (स्पर्श रेखा तथा अभिलम्ब )
- MULTIPLE CHOICE QUESTIONS(प्रतिस्थानपन द्वारा अवकलन, उच्च कोटि के अवकलज )