Complete Solutions to SOLVED MULTIPLE CHOICE QUESTIONS (वक्रों द्वारा परिबद्ध क्षेत्रफल ) of chapter निश्चित समाकलन एवं वक्रों से घिरा क्षेत्रफल of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | निश्चित समाकलन एवं वक्रों से घिरा क्षेत्रफल |
| ERRORLESS HINDI | SOLVED MULTIPLE CHOICE QUESTIONS (वक्रों द्वारा परिबद्ध क्षेत्रफल ) |
| Number Of Questions | 97 |
| Academic Year | 2023-24 |
वक्र `y = xe^(x^2)` , x- अक्ष तथा कोटियों x = 0, x = a से घिरा क्षेत्रफल है
View Solutionx = 0 तथा `x =2pi` के बीच वक्र y = sin x से घिरा क्षेत्रफल है
View Solutionयदि `y = (1-x)^(2),y=0` और x= 0 द्वारा परिबद्ध क्षेत्र को सरल रेखा x =b दो भागों `R_(1)(0 le x le b)` और `R_(2) (b le x le 1)` में इस प्रकार विभाजित करती है कि `R_(1) - R_(2) =1/4` तो b का मान है.
View Solutionयदि कोटि x=a वक्र `y =(1+8/(x^2))` x-अक्ष तथा कोटियों x=2, x=4 से घिरे क्षेत्रफल को समद्विभाजित करती हो, तो
View Solutionवक्र `y= cosx` तथा x-अक्ष से घिरे क्षेत्र का क्षेत्रफल क्या होगा, जबकि `0 le x le 2 pi`
View Solutionपरवलय `(y-2)^(2)=x-1`, परवलय कि बिन्दु `(2,3)` पर स्पर्श रेखा और x-अक्ष द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है -
View Solutionवक्र xy =c, x-अक्ष और रेखाओं x=1 और x = 4 के मध्य स्थित क्षेत्रफल है
View Solutionमान लीजिए कि `f:[-1,2] rarr [0, oo)` एक ऐसा सतत् फलन है जो कि अन्तराल [-1,2] में x के सभी मानों के लिये f(x) = f(1-x) को संतुष्ट करता है। यदि `R_(1) = int_(-1)^(2)xf (x)dx` है और `R_2` उस क्षेत्र का क्षेत्रफल है जो y= f(x), x =-1,x=2 तथा x-अक्ष द्वारा परिबद्ध है, तब
View Solutionवक्र y= sin2x+ cos 2x तथा x=0 और `x = pi/4` के बीच घिरा क्षेत्रफल है
View Solutionवक्र `y = sqrt(3x+4)` तथा x=0 व x= 4 के बीच घिरा क्षेत्रफल है
View Solutionरेखाओं `y= 2+x, y = 2 - x` और x=2 से परिबद्ध क्षेत्रफल है
View Solutionवक्रों y= cosx और y cos2x के x = 0 `x = pi//3` तथा x - अक्ष से घिरे क्षेत्रों का अनुपात है
View Solutionवक्र `y=x^3` x-अक्ष तथा कोटियों x =1 व x=2 से घिरे क्षेत्र का क्षेत्रफल है
View Solutiony=|sin x|, x-अक्ष एवं रेखाओं `|x| = pi` से परिबद्ध क्षेत्रफल है
View Solutionपरवलय `y^(2) = 4ax` , इसके अक्ष और दो कोटियों x =4, x=9 से घिरे क्षेत्र का क्षेत्रफल है
View Solutionरेखा y= x तथा y = x+sin x से घिरे क्षेत्र का क्षेत्रफल होगा (जहाँ `0 le x le pi` )
View Solutionवक्र y= tanx तथा x-अक्ष से घिरे क्षेत्र का क्षेत्रफल (जहाँ - `pi//3 le x le pi//3`) होगा
View Solutionयदि वक्र `y = asqrt(x) + bx` , बिन्दु (1, 2) से होकर गुजरता है तथा वक्र, सरल रेखा x =4 तथा x-अक्ष के बीच घिरे क्षेत्र का क्षेत्रफल 8 वर्ग इकाई है, तब
View Solutionयदि x-अक्ष के ऊपर, वक्रों `y = 2^(kx)` तथा x = 0 व_x =2 से परिबद्ध क्षेत्र का क्षेत्रफल `3/(ln2)` हो, तो k का मान है
View Solutionयदि वक्र y = f(x), सरल रेखा x=1,x = b तथा x-अक्ष से घिरे । क्षेत्र का क्षेत्रफल `sqrt(b^2+1) -sqrt2` है, (सभी `b gt 1`) तब f{x) =
View Solutionयदि फलन `y= f(x)` का `x-`अक्ष, `x = 1` तथा `x = b` के बीच घिरे क्षेत्र का क्षेत्रफल `(b - 1) sin (3b +4)` है तब `f(x) =`
View Solutionवक्र `x^(2) = 4y` , रेखा `x = 2` और `x-`अक्ष के बीच घिरे क्षेत्र का क्षेत्रफल (वर्ग इकाई में) है `:`
View Solutionवक्र `y= x^(2) - 4x` , `x-`अक्ष एवं रेखा `x = 2` द्वारा घिरा क्षेत्रफल है `:`
View Solutionवक्र xy-3x-2y-10 = 0, x-अक्ष तथा रेखाओं x=3,x = 4 से घिरा क्षेत्रफल है
View Solutionवक्र `y^2 =x` रेखा y=4 तथा y-अक्ष द्वारा परिबद्ध क्षेत्रफल है
View Solutionनिर्देशांक अक्षो तथा वक्र `y = log_(e)x` से परिबद्ध क्षेत्रफल है
View Solutionसरल रेखाओं x = 0,x=2 तथा वक्रों `y=2^(x),y = 2x-x^(2)` से परिबद्ध क्षेत्रफल है
View Solutionवक्रों y =x,x =e,y = `1/x` तथा x-अक्ष की धन दिशा के बीच घिरे क्षेत्र का क्षेत्रफल है
View Solutionवक्र `y = sin^3` x, x-अक्ष तथा x=0 से `x = pi/2` द्वारा परिबद्ध क्षेत्रफल है
View Solutionवृत्त `x^2 + y^2 = 4` , रेखा `x=sqrt(3y)` तथा x-अक्ष द्वारा प्रथम पाद में घिरे क्षेत्र का क्षेत्रफल होगा
View Solutionअतिपरवलय `xy = a^2` पर खींची गई स्पर्श रेखा तथा निर्देशांक अक्षों द्वारा बने त्रिभुज का क्षेत्रफल है
View Solutionवक्रों y = sin x,y = cos x तथा x = 0 द्वारा परिबद्ध त्रिभुजाकार क्षेत्र का क्षेत्रफल है
View Solutionवक्र `y=4x-x^2` तथा x-अक्ष के बीच का क्षेत्रफल होगा
View Solutionवक्र `y = tan x` पर स्थित बिन्दु `x=pi/4` पर खींची गए स्पर्श रेखा तथा x - अक्ष से घिरे क्षेत्र का क्षेत्रफल है
View Solutionवक्रों `y = xlog x` एवं `y = 2x -2x^2` द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
View Solutionवक्र y = x , x - अक्ष तथा कोटियों x = -1 व x = 2 से परिबद्ध क्षेत्र का क्षेत्रफल है
View Solutionपरवलय `y^(2) =4ax` रेखा x = a और x=4a के बीच घिरा क्षेत्रफल है
View Solution`y = -x^2+2x+3` और y = 0 से घिरा क्षेत्रफल है
View Solutionयदि वक्रों `y = mx^2 ` तथा `x = my^(2) ( m gt 0)` के मध्य क्षेत्रफल `1/4` वर्ग की इकाई है , तब m का मान है
View Solutionपरवलय `y=x^2` और y = x रेखा के बीच घिरे क्षेत्र का क्षेत्रफल है
View Solutionपरवलय `y^2 = 4ax` तथा इसकी नाभिलम्ब जीवा से घिरा क्षेत्रफल है
View Solution`ay=3(a^2-x^2)` तथा x- अक्ष से घिरे क्षेत्रफल है
View Solutionदीर्घवृत्त `(x^2)/(a^2)+y^2/b^2=1` का क्षेत्रफल है
View Solutionसमीकरण `y = |x-1|` तथा `y = 1` से घिरे क्षेत्र का क्षेत्रफल होगा
View Solutionपरवलयों `y = 4x^(2), y=x^2/9` तथा रेखा y = 2 से प्रतिबद्ध क्षेत्रफल है
View Solutionवक्र `xy^2 =a^(2)(a-x)` एवं y- अक्ष से घिरे क्षेत्र का क्षेत्रफल होगा
View Solutionपरवलयों `y =x^2-1` तथा `y = 1 -x^2` से परिबद्ध क्षेत्रफल है।
View Solutionरेखा x = 1 तथा वृत `x^(2)+y^(2)=9` से घिरे लघु भाग का क्षेत्रफल है
View Solutionवक्र `y=|x- 2|,x=1,x=3` x-अक्ष के बीच घिरे क्षेत्र का क्षेत्रफल है
View Solutionवक्रों `y^(2) -8x` एवं `x^(2) =8y` द्वारा परिबद्ध क्षेत्रफल है
View Solutionवक्र `y^(2) = 8x` और y = x के बीच घिरे का क्षेत्रफल है
View Solutionवक्रों `y = log_(e) x` तथा `y = (log_(e)x)^2` द्वारा घिरे क्षेत्र का क्षेत्रफल है
View Solutionपरवलय `y^(2) = 4x ` तथा `y = 2x-4` रेखा के बीच प्रतिबद्ध क्षेत्रफल बराबर है
View Solutionवक्रों `y = x^(2) ` तथा `y = |x|` से घिरे क्षेत्र का क्षेत्रफल है `:`
View Solutionकोटियों x = 0 तथा `x = (3pi)/2` के बीच वक्रों y = cos x तथा y = sin x से घिरे क्षेत्र का क्षेत्रफल है
View Solutionप्रथम चतुर्थाश में `x^(2) +y^(2)=pi^2` एवं `y = sinx ` के बीच घिरा क्षेत्रफल है
View Solutionवक्रों `x +2y^(2) =0` तथा `x +3y^2 =1` के बीच घिरे तलीय क्षेत्र का क्षेत्रफल है
View Solution`A = {(x,y) :x^2+y^(2) le 1` तथा `y^2=1-x` } के द्वारा प्रदत्त क्षेत्र का क्षेत्रफल है
View Solutionपहले चतुर्थांश में वक्रो `y = sin^(-1) x +x (1-x)` और `y = sin^(-1) x -x (1-x) ` द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
View Solution`2|x| + 3 | y | le 6` से प्रतिबद्ध क्षेत्रफल है
View Solutionअन्तराल `[0,(pi)/2]` पर वक्रों `y = sinx + cos x ` तथा ` y = |cos x - sinx|` द्वारा परिबद्ध क्षेत्रफल है
View Solutionयदि `f(x)=x^(2//3), x ge 0` तब y = f(x) वक्र एवं तीन रेखाओं y = x, x = 1 तथा x = 8 से घिरे क्षेत्र का क्षेत्रफल होगा
View Solutionवक्र `y = 2x-x^2` तथा x-अक्ष से घिरे क्षेत्र है
View Solutionवक्र `y = x^3` से घिरे क्षेत्र का क्षेत्रफल है , जिसकी स्पर्श रेखा वक्र को बिन्दु (1,1) स्पर्श करती हुई X - अक्ष को काटती है
View Solution`y = |x| ` और `y =-|x|+2` से घिरे क्षेत्र का क्षेत्रफल है वर्ग इकाई
View Solution`y =x^(3) , y = 8` तथा x = 0 से घिरे क्षेत्र है
View Solution`{x,y:y^(2) le 2x` तथा `y ge 4x-1}` द्वारा परिभाषित क्षेत्र का क्षेत्रफल (वर्ग इकाईयों) में है
View Solution`y^(2) =16 -x^2` तथा y = 0 , x = 0 से प्रथम चतुर्थांश में घिरे क्षेत्र का क्षेत्रफल (वर्ग इकाई में) है
View Solutionरेखाओं `y -2x = 2, y = 4` तथा y- अक्ष से घिरे क्षेत्र का क्षेत्रफल है
View Solutionवक्रों `y^(2) = 2x` तथा y = x से घिरे क्षेत्र का क्षेत्रफल है
View Solutionक्षेत्र `{(x,y): y^2 ge 2x` तथा `x^2+y^2lt 4x , x ge 0 , y ge 0` } का क्षेत्रफल (वर्ग इकाईयों में ) है
View Solution`y=sqrt(5-x^2)` तथा y = |x-1| से घिरा क्षेत्र है
View Solutionव्रक `x^2=4y` और सरल रेखा `x = 4y -2` द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
View Solutionवक्र `y = sqrt(16 -x^2)` और X- अक्ष से परिबद्ध क्षेत्र का क्षेत्रफल है
View Solutionप्रथम चतुर्थांश में X - अक्ष, रेखा y = x और वृत `x^(2) +y^(2) = 32` द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
View Solutionव्रक y = cos द्वारा x = 0 और `x = pi ` की बीच में परिबद्ध क्षेत्र का क्षेत्रफल है
View Solutionपरवलय `y^2 = x` और सरल रेखा 2y =x से परिबद्ध क्षेत्र का क्षेत्रफल है
View Solutionवक्र y = sin x द्वारा कोटि x = 0, x = `pi/2` तथा X-अक्ष के बीच परिबद्ध क्षेत्र का क्षेत्रफल है
View Solutionदीर्घवृत्त `(x^2)/(25)+y^2/(16)=1` द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
View Solutionवृत `x^2+y^2=1` द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
View Solutionव्रक y = x+ 1 तथा x = 2 , x = 3 रेखाओं एवं x अक्ष द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
View Solutionव्रक x = 2y + 3 , y = 1 और y = -1 रेखाओं द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
View Solutiony=||x-3|-4|-5 और X-अक्ष द्वारा परिबद्ध क्षेत्रफल है
View Solutionत्रिज्या R वाले किसी वृत्त के अंतर्गत बने सभी चक्रीय चतुर्भुजों जिनके एक कोण का मान `120^@` है, में से सबसे अधिक क्षेत्रफल वाले चतुर्भुज का क्षेत्रफल है
View Solutionपरवलय `y = x^2` और `y =1-x^2` द्वारा परिबद्ध क्षेत्रफल है
View Solutionकिसी समतल पर क्षेत्र `A= {(x,y)|x^(2) +y^(2)lt 100} ` है और क्षेत्र `B= {(x,y|sin(x +y) > 0}` है, तो क्षेत्र `A capB` का क्षेत्रफल क्या
View Solutionनिम्नलिखित आरेख में [1,3] अंतराल पर y= f(x) सतत फलन दिखाया गया है। A,B,C के निर्देशांक क्रमशः (1, 1), (3, 2) और (2, 3) हैं: `L_1` और `L_2` रेखाएँ समांतर हैं, `L_1` स्पर्श रेखा है जो C पर वक्र को स्पर्श करती है। यदि y= f(x) आलेख के नीचे का क्षेत्रफल x=1 से x=3 तक 4 वर्ग इकाई है, तो आच्छादित क्षेत्र का क्षेत्रफल क्या है
View Solutionयदि `0 le x le 3` हो, तो वक्र `y=|x^(3) -4x^(2) +3x|` एवं x-अक्ष के बीच का क्षेत्रफल होगा
View Solutionउन सभी त्रिज्याखण्डों पर विचार करें जिनका परिमाप का परिमाण स्थिर है, तब इनमें से अधिकतम क्षेत्रफल वाले त्रिज्याखण्ड के कोण का मान ज्ञात करें (अर्थात् त्रिज्याखण्ड के दो सीमांकन त्रिज्याओं के बीच का कोण)
View Solutionएक क्षेत्र, जो वक्र y = cosx तथा दो रेखाओं जो कि बिन्दुओं `(-pi //4, cos(-pi//4))` और (0, 2) तथा बिन्दुओं `(pi//4,cos (pi//4))` और (0, 2) को जोड़ती है, से घिरा हुआ है, इस क्षेत्र का क्षेत्रफल होगा
View Solutionवृत्त `C_0` की त्रिज्या 1 है। प्रत्येक पूर्णांक `n ge 1` के लिए `C_n` एक ऐसा वृत्त है जिसका क्षेत्रफल उस वर्ग के क्षेत्रफल के बराबर है जो `C_(n-1)` में अंतर्गत किया गया है, तब ऐसी स्थिति में दी गई अनन श्रेणी `sum_(1=0)^(oo) (C_i` का क्षेत्रफल) का मान होगा
View Solutionमान ले कि वक्र `y = 1/x` और रेखाएँ `y = 0, x = 1, x = 10` द्वारा परिबद्ध क्षेत्रफल A है , माना `B = 1+1/2 + .......+1/9` और `C = 1/(2) +1/(3) + ........ + 1/(10)` है , तब
View Solutionत्रिभुज ABC में G उसका केन्द्रक है और खंड AB,AC पर M,N क्रमशः इस प्रकार हैं कि M,G,N संरेखीय हैं। यदि त्रिभुज AMN और त्रिभुज ABC के क्षेत्रफलों का अनुपात r है.
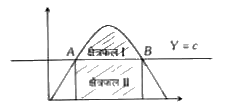
View Solutionफलन `y=2x-4x^(3)` के ग्राफ का एक भाग दी गयी आकृति में दर्शाया गया है। रेखा y =c इस प्रकार है कि क्षेत्र I, II के क्षेत्रफल बराबर हैं। यदि बिन्दु A,B के x-निर्देशांक क्रमानुसार a,b हैं, तो a+b का मान होगा
View SolutionO केंद्र के एक वृत्त में तीन बिन्दु A,P,B वृत की परिधि पर इस प्रकार स्थित है कि बिन्दु P लधु चाप AB का मध्य बिन्दु है माना जब `angleAOB = theta` हो , तो
`("क्षेत्रफल" (DeltaAOB))/("क्षेत्रफल"(DeltaAPB))=sqrt5+2` यदि `angleAOB ` को `2theta` कर दिया जाए , तो `("क्षेत्रफल" (DeltaAOB))/("क्षेत्रफल"(DeltaAPB)) ` का मान होगा
View Solutionक्षेत्र `{(x,y) : x ge 0 , x+ y le 3,x^2le 4y` तथा `y le 1 + sqrtx` } का क्षेत्रफल (वर्ग इकाइयों ) में है
View Solutionमाना `g(x) = cosx^(2),f(x) = sqrt(x)` तथा `alpha , beta (alpha lt beta)` द्विघाती समीकरण `18x^(2)-9pix + pi^2 =0` के मूल हैं। तो वक्र `y= (gof)(x)` तथा रेखाओं `x = alpha , x = beta` तथा y=0 द्वारा घिरे क्षेत्र का क्षेत्रफल (वर्ग इकाइयों में) है
View Solution
SOLVED MULTIPLE CHOICE QUESTIONS (वक्रों द्वारा परिबद्ध क्षेत्रफल ) questions and complete solutions for chapter निश्चित समाकलन एवं वक्रों से घिरा क्षेत्रफल of ERRORLESS MATHS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 MATHS निश्चित समाकलन एवं वक्रों से घिरा क्षेत्रफल
- EXERCISE
- ILLUSTRATION
- JEE ADVANCED (Comprehension type questions)
- JEE ADVANCED (Integer type questions)
- JEE ADVANCED (Matrix Match type questions)
- JEE ADVANCED (More than one correct answers)
- JEE ADVANCED (Reasoning type questions)
- SOLVED MULTIPLE CHOICE QUESTIONS
- SOLVED MULTIPLE CHOICE QUESTIONS (निश्चत समाकलन के प्रगुण )
- SOLVED MULTIPLE CHOICE QUESTIONS (वक्रों द्वारा परिबद्ध क्षेत्रफल )