Complete Solutions to प्रश्न of chapter PAPER (8 APRIL SHIFT -2) of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PAPER (8 APRIL SHIFT -2) |
| ERRORLESS HINDI | प्रश्न |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
वृत `x^(2) + y^(2) =4` के बिन्दु `(sqrt(3),1)` पर खीची गई स्पर्श रेखा और अभिलंब तथाx- अक्ष एक त्रिभुज बनाते है। इस त्रिभुज का क्षेत्र फल (वर्ग इकाईया है। )
View Solutionयदि `f(1) =1 f(1) =3` है तो `f(f(f(x)))+ (f(x)^(2)` का x=1 पर अवकलज है।
View Solutionएक विधार्थी पाँच परीक्षाओं में निम्न अंक प्राप्त करता है। 45 ,54, 41 , 57, 43 उसके द्वारा छटी परीक्षा में प्राप्त अंको का माध्य 48 है। तो छ परीक्षाओं में प्राप्त अंको का मानक विचलन है।
View Solutionयदि एक दीर्घवृत जिसका केन्द्र मूलबिन्दु पर हैं दीर्घ अक्ष तथा लघु अक्ष की लम्बाईया का अंतर 10 है तथा एक नामिकेन्द्र `(0,5sqrt(3))` पर है तो इसके नामिकेन्द्र की लम्बाई है।
View Solutionपरवलय `y^(2) =4x` के उस बिन्दु जहॉ। यह वृत `x^(2)+y^(2)=5` का प्रथम चतुर्भया में काटता है। पर खीची गई स्पर्श रेखा बिन्दु से हेाकर जाती है।
View Solutionनिम्न कथनों में से कौन-सा एक पुनरूवित नही है।
View Solutionएक अनभिनत सिक्के को कम से कम कितनी बार उछाला जाए ताकि कम से कम शीर्ष आने की प्रायिकता कम से कम 90% हों
View Solutionमाना `f(x) = underset(0 ) overset(x )(int ) g (t ) dt` जहॉ। g एक शून्येत्तर समफल है। यदि `f(x+5) = g (x )` है तो ` underset(0 ) overset(x ) (int) f (t) dt` बराबर है
View Solutionयदि तीन भिन्न संख्याए a,b,c गुणोतर श्रेणी में हैं समीकरण `ax^(2) + 2bx + c = 0` और `dx^(2) + 2ex + f = 0` का एक उभयनिष्ठ मूल है। तो निम्न में सें कौन –सा एक कथन सत्य है।
View Solutionमाना `f: R to R ` एक अवकलनीय फलन है तो कि `f(3) + f (2) = 0` को संतुष्ट करता हैं तो `underset(x to 0 ) (lim) .((1+f(3+x)-f(3))/( 1+f(2+x)-f(2)))` बराबर है।
View Solutionमाना किसी वास्तविक संख्या `x ` के लिए `bar(a ) = 3 hat(I ) + 2hat(j ) + xhat(k)` तथा `hat(b ) = hat(I ) - hat(j ) + hat(k )` है तो `|vec( a) xx vec( b)|` तभी सम्भव है जब
View Solutionयदि एक समकोणीय त्रिभुज की भुजाएँ समान्तर श्रेणी में है , तो उनका अनुपात होगा -
View Solutionमाना `f : (1-1,3)to R ` इस प्रकार परिभाषित है कि
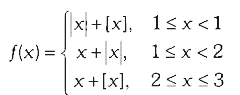 जहॉ। (t ) , t से कम या बराबर पुर्णाक को दर्शाता हैं है तो असतल है।
जहॉ। (t ) , t से कम या बराबर पुर्णाक को दर्शाता हैं है तो असतल है।
View Solutionमाना बिंदु (h, k ) ,(1,2) तथा (-3,4) एक रेखा `L_(1)` पर स्थित हैं यदि बिन्दुओं (h, k) तथा (4,3) से होकर जानते वाली रेखा `L_(2)` रेखा `L_(1)` के लम्बवतल है तो `(k)/(h)` बराबर हैं
View Solutionअंको 0,1,2,3,4,5 का प्रयोग करके (जहाँ अंको को दोहराया जा सकता है) बनाई जा सकने वाली चार अंको की संख्याओं, जो 4321 से अधिक (strictly greater) हो, की संख्या है
View Solutionमाना `S(alpha)= {(x,y) : y^(2) le x , 0 le xx le alpha )` तथा ` A (alpha) ` क्षेत्र `S(alpha)` का क्षेत्र फल है। यदि किसी `lambda 0, le lambda lt 4` के लिए `A (lambda) : A (4 ) = 2:5` है तो `lambda` बराबर है।
View Solutionयदि `int (dx )/( x^(3) (1+x^(6))^(2//3))= x (x ) (1+x)^(6) + c` जहॉ। C एक समाकलन अचर हैं तो फलन f(x ) बराबर है।
View Solutionमाना संख्याऍं 2,b,c एक समान्तर श्रेणी में है तथा `[{:(1,1,1),(2,b,c),(4,b^2 , c^2):}]` यदि `det (A ) EE [1,16]` तो c निम्न में से किस अन्तराल मे है।
View Solutionयदि `z= (sqrt(3))/(2) + (1)/(2) (i= sqrt(-1))` तो `(1+iz+ z^(5)+iz^(8))^(9)` बराबर है।
View Solutionयदि `(sqrt((1)/(x^(1+log 10 x) ))+ x^(1/12))^(6)` के दिपद प्रसार का चौथा पद 200 है। तथा `x gt 1` है तो x का मान है।
View Solutionएक गोले जिसकी त्रिज्या 3 है के अंतर्गत बने अधिकतम आयतन के लंबवृततीय बेलन की ऊँचाई है।
View Solutionयदि रैखिक समरीकरण निकाया
`x-2y + kz=1`
`2x+y+z=2`
`3x-y -kz=3`
का एक हल (x,y,z) z`ne 0` है तो `(x,y)` जिस रेखा पर स्थित है उसका समीकरण है।
View Solutionसमतलों x+y +z=1 तथा 2x+ 3y+4z=5 की प्रतिच्छेद रेखा से होकर जाने वाले तथा समतल x-y+z =0 लंबवत समतल का सदिश समीकरण है।
View Solutionयदि बिन्दु `(4,6)` से होकर जाने वाले मानक अतिपरवल्य की उत्केन्द्रता 2 हैं तो `(4,6)` पर अतिपरवल्य पर खीची गई स्पर्श रेखा का समीकरण हैं
View Solutionयोग `underset(k=1)overset(20)Sigma k (1)/(2^(k))` बराबर है
View Solutionमाना `f(x) = a^(x ) (a gt 0)` को `(f (x ) = f_(1) + f_(2) (x)` के रूप मे लिखा गया है जबकि `f_(1)(x)` एक सम फलन है। और `f_(2) (x )` का विषम फलन है। तो `f_(1) (x+y) + f_(1) (y-x)` बराबर है।
View Solutionयदि एक बिन्दु `R(4,y,z)` बिन्दुओं `P(2,-3,4)` तथा Q(8,0,10) को मिलाने वाले रेखाखण्ड पर स्थित हैं तो R की मूलबिन्दु से दूरी है।
View Solution20mतथा 80 m ऊँचाई वाजे दो खंभे एक क्षेतिज समतल पर सीधे खडे है। हैं प्रत्येक खंभे शिखर को दूसरे खंभे के पाद से मिलाने वाली रेखाओं के प्रतिच्छेद बिन्दु की इस समतल से ऊँचाई मीटारो में है।
View SolutionM के उन पूर्णक मानो की संख्या जिनके लिए समीकरण `(1+m^(2)) x^(2) -2(1+3m)x + (1+8m)=0` के कोई भी वास्तविक मूल नही है।
View Solutionयदि वक्र `y=y(x)` के किसी बिन्दु `(x,y)` पर खीची गई स्पर्श रेखा की प्रवणता `(2y)/( x^(2))` हैं। यदि वक्र, वृत्त `x^(2) + y^(2) - 2x - 2y=0` के केन्द्र से होकर जाता है तो वक्र का समीकरण है।
View Solution
प्रश्न questions and complete solutions for chapter PAPER (8 APRIL SHIFT -2) of ERRORLESS MATHS (HINDI) of Class 12