Complete Solutions to Ordinary Thinking ( सदिश गुणन ) of chapter गणितीय अवधाराणाएं एवं सदिश of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | गणितीय अवधाराणाएं एवं सदिश |
| ERRORLESS HINDI | Ordinary Thinking ( सदिश गुणन ) |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
यदि एक सदिश `2hati+3hatj+8hatk` दूसरे सदिश `4hatj-4hati+alpha hatk` पर लम्बवत हो तो `alpha` का मान होगा
View Solutionदो सदिश `vecA` व `vec B` के मान `vecA=2hati+3hatj` तथा `vecB=hati+hatj` है। `vecB` के अनुदिश `vecA` के घटक का परिमाण है
View Solutionयदि `hati,hatj` व `hatk` क्रमशः x,y व z- अक्ष के अनुदिश इकाई सदिश है तब सदिशों `hati+hatj+hatk` तथा `hati+hatj` के मध्य कोण `theta` होगा
View Solutionएकसमान बल `(4hati+hatj+3hatk)N` के अंतर्गत कोई कण स्थिति `3hati+2hatj-6hatk` से `14hati+13hatj+9hatk` तक गति करता है। यदि विस्थापन मीटर में हो तो किया गया कार्य होगा।
View Solutionयदि दो सदिशों `vecA` तथा `vecB` का योग सदिश `(vecA+vecB)` इनके अंतर सदिश `(vecA-vecB)` के लम्बवत हो तो इनके परिमाणों का अनुपात है
View Solutionसदिश `vecA` और `vecB` के बीच का कोण `theta` हो तो त्रिक गुणनफल `vecA.(vecBxxvecA)` का मान होगा
View Solutionयदि `vecAxxvecB=vecBxxvecA` हो तो `vecA` व `vecB` के बीच का कोण होगा
View Solutionसदिश `vecA` तथा `vecB` परस्पर `theta` कोण अंतरित करते हैं इनके लिये निम्न में से कौन सा कथन सत्य है
View Solutionएक कण X-Y समतल में किसी बल के कारण इस प्रकार गतिमान है कि उसका रेखीय संवेग `vecP(t)=A[haticos (kt)-hatj sin (kt)]` है जहां A और k नियतांक है तोबल और संवेग के बीच कोण होगा
View Solutionयदि `vecAxxvecB=vecC` तो निम्न में से कौन सा कथन गलत है
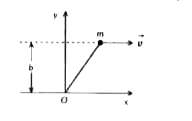
View Solutionm द्रव्यमान का एक कण x-y तल में नियत वेग v से x-अक्ष के समांतर चित्रानुसार गति कर रहा है किसी समय t पर मूल बिंदु के सापेक्ष इसका कोणीय संवेग होगा
View Solution5 इकाई परिमाण का सदिश `vecAxy-` समतल के अनुदिश और बिंदु x को ओर बढ़ती हुई दिशा से `120^(@)` पर है। सदिश `vecB` जिसका परिमाण 9 इकाई तथा बिंदु z- अक्ष के सापेक्ष है तब `vecAxxvecB` के गुणनफल का परिमाण होगा
View Solutionएक सदिश `vecF=4hati-3hatj` है सदिश `vecF` के लम्बवत अन्य सदिश है
View Solutionसदिश `veca=3veci-4vecj` और `vecb=-2veci+3veck` के मध्य कोण है
View Solutionसदिश `vecA` और `vecB` इस प्रकार है कि `|vecA+vecB|=|vecA-vecB|` तो सदिशों के बीच कोण है।
View Solutionबल `vecF=(5hati+3hatj)` न्यूटन एक कण पर लगाया जाता है तो इसे मूल बिंदु से `vecr=(2hati-1hatj)` मीटर तक विस्थापित कर देता है। बल द्वारा किया गया कार्य होगा
View Solution`vecA` और `vecB` दो सदिश है जिनके बीच का कोण `theta` है यदि `|vecAxxvecB|=sqrt(3)(vecA.vecB)` हो तो `theta` का मान होगा
View Solutionयदि सदिश `vecA=cos omega hati +sin omega hatj` तथा सदिश `vecB="cos"(omega t)/2+"sin"(omega t)/2hatj` समय के फलन है तो t का वह मान क्या होगा जिस पर ये सदिश परस्पर लंबकोणि होगें
View Solutionएक कण नियत बल `vecF=(20hati+15hatj-5hatk)N` के प्रभाव में वेग `(6hati-4hatj+3hatk)m//s` से गति करता है। कण पर आरोपित तात्क्षणिक शक्ति है ( तात्क्षणिक शक्ति के लिए `P=vecF.vecv` का प्रयोग करे )
View Solution`(vecA+vecB)xx(vecA-vecB)` का मान है
View Solutionकिसी कण की स्थिति `vecr=(hati+2hatj-hatk)` तथा संवेग `vecP=(3hati+4hatj-2hatk)` है तो कोणीय संवेग निम्न के लम्बवत होगा
View Solutionदो सदिशों `vecA=5hati+5hatj` तथा `vecB=5hati-5hatj` के बीच कोण होगा।
View Solutionयदि`|vec(A)xxvec(B)|= sqrt(3)vec(A).vec(B)` हो , तो`|vec(A)+vec(B)|` का मान होगा -
View Solutionसदिश `2hati+2hatj-hatk` तथा `6hati-3hatj+2hatk` के लम्बवत इकाई सदिश होगा
View Solutionबिंदु `vecr=7hati+3hatj+hatk` पर कार्य करने वाले बल `vecF=-3hati+hatj+5hatk` का आघूर्ण होगा
[ यदि बल आघूर्ण `vec(tau)=vecrxxvecF` हो ]
View Solutionसदिशों `vecA=2hati+3hatj` तथा `vecB=hati+4hatj` द्वारा प्रदर्शित समांतर चतुर्भुज का क्षेत्रफल होगा।
View Solutionसदिश `vecA,vecB` तथा `vecC` इस प्रकार है कि `vecA.vecB=0` तथा `vecA.vecC=0` तो `vecA` के समांतर सदिश है
View Solutionयदि दो सदिशों `vecA` तथा `vecB` के लिए `vecAxxvecB=0`, हो तो सदिश
View Solutionसदिश `(vecAxxvecB)` तथा `(vecBxxvecA)` के बीच कोण है
View Solutionजब `vecA.vecB=-|vecA||vecB|` तब
View Solutionदो सदिशों के परिमाण क्रमशः 2 तथा 3 है। यदि इनका परिणामी 1 हो तो उनका सदिश गुणनफल होगा
View Solutionसदिश जो `(a cos theta hati+b sin theta hatj)` के लम्बवत है
View Solutionदो परस्पर लम्बवत सदिशों का अदिश गुणनफल होगा।
View Solutionएक सदिश `vecA` ऊर्ध्वाधर ऊपर की ओर इंगित है तथा `vecB` उत्तर की ओर। सदिश गुणनफल `vecAxxvecB` है
View Solutionस्थिति सदिश `vecr=(3hati+4hatj)` पर स्थित एकांक द्रव्यमान वेग `vecv=(5hati-6hatj)` से गति कर रहा है । मूल बिंदु के सापेक्ष पिण्ड का कोणीय संवेग होगा।
View Solutionयदि `vec(omega)=3hati-4hatj+hatk` तथा `vecr=5hati-6hatj+6hatk` तब रेखीय वेग का मान होगा
View Solution
Ordinary Thinking ( सदिश गुणन ) questions and complete solutions for chapter गणितीय अवधाराणाएं एवं सदिश of ERRORLESS PHYSICS (HINDI) of Class 12