Complete Solutions to Critical Thinking (Objective Questions) of chapter द्वि-विमीय गति of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | द्वि-विमीय गति |
| ERRORLESS HINDI | Critical Thinking (Objective Questions) |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
एक वेग `vecv=K(y hati+x hatj)` जहां K एक स्थिरांक है। इसके पथ का सामान्य समीकरण है
View Solutionएक L लम्बाई की नलिका में M द्रव्यमान का असम्पीड्य द्रव भरा है तथा नली दोनों सिरों पर बन्द है। अब नली को इसके एक सिरे के सापेक्ष क्षैतिज तल में एकसमान कोणीय वेग से घुमाया जाता है, तो द्रव द्वारा दूसरे सिरे पर आरोपित बल होगा
View SolutionR त्रिज्या के वृत्तीय मार्ग पर गति करते हुए कण की गतिज ऊर्जा K, इसके द्वारा तय की गई दूरी पर `K= as^2` के अनुसार निर्भर करती है, जहाँ a अचर है। कण पर कार्य करने वाला बल है
View Solutionएक कार 10 मीटर त्रिज्या के वृत्तीय क्षैतिज मार्ग पर समान चाल 10 मीटर/सेकण्ड से गति कर रही है। कार की छत से 1 m की दृढ़ छड़ से एक लोलक लटका है, तो पथ से छड़ द्वारा बनाया गया कोण है
View Solutionएक घडी की सैकण्ड की सुई और घण्टे की सुई की कोणीय गति का अनुपात होता है
View SolutionL लम्बाई की एक डोरी एक सिरे पर बंधी हुई है एवं इसके दूसरे सिरे पर M द्रव्यमान लटका है। डोरी स्थिर सिरे से गुजरने वाले ऊर्ध्वाधर अक्ष के परितः (चित्रानुसार) `2//pi` चक्कर प्रति सैकण्ड पूर्ण करती है। डोरी में तनाव है :
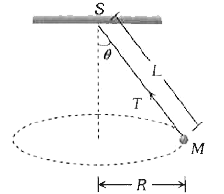
View Solutionएक प्रक्षेप्य को पृथ्वी की सतह से `5ms^(-1)` के वेग से तथा क्षैतिज दिशा से कोण पर छोड़ा जाता है। किसी अन्य ग्रह से `3ms^(-1)` के वेग तथा इसी कोण `(theta)` पर छोड़े गये एक प्रक्षेप्य का प्रक्षेप पथ, पृथ्वी से छोड़े गये एक प्रक्षेप्य के प्रक्षेप पथ के सर्वसम (सर्वधा समान) है। यदि पृथ्वी पर `g=9.8 ms^(-2)` है तो, इस ग्रह पर गुरूत्वीय त्वरण का मान `ms^(-2)` में होगा|
View Solutionएक डिस्क अपने केन्द्र O पर एक समान कोणीय चाल `omega` से घूम रही है। इसके व्यास के एक तरफ आच्छादित व दूसरी तरफ अन-आच्छादित क्षेत्र हैं (चित्र देखिए)। जब डिरक चित्र में दर्शायी गई अवस्था में हैं तब दो कंकड़ P और Q एक ही समय पर y-z तल में R की तरफ एक- कोण पर प्रक्षेपित किये जाते हैं। दोनों का वेग डिस्क के सापेक्ष बराबर है। मानें कि (i) डिस्क के `1/8` चक्कर काटने से पहले कंकड़ डिस्क पर वापस आ गिरते हैं, (ii) उनका परास डिस्क की त्रिज्या के आधे से कम है, और (iii) वही बना रहता है। तब
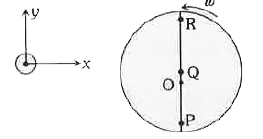
View Solutionएक लम्बी एवं क्षैतिज छड़ पर एक मोती रखा है जो इसकी लम्बाई के अनुदिश फिसल सकता है, प्रारम्भ में यह मोती छड़ के एक सिरे A से L दूरी पर स्थित है। छड़ को एक एमान कोणीय त्वरण `alpha` से सिरे A के परितः कोणीय गति प्रदान की जाती है। यदि छड़ एवं मोती के बीच घर्षण गुणांक `mu` है एवं गुरुत्व नगण्य है, तब कितने समय पश्चात् मोती फिसलने लगेगा
View Solutionएक छोटे गुटके को चित्र में दिखाए गये चार मागों के अनुदिश देगा जाता है। प्रत्येक मार्ग समान ऊँचाई तक उठा हुआ है। सभी स्थितियों में, मार्ग में प्रवेश करते समय गुटके का वेग समान है। किस स्थिति में मार्ग के उच्चतम बिन्दु पर अभिलम्य प्रतिक्रिया अधिकतम है।
View Solutionएक सरल लोलक नियत आयाम (बिना मंदन के) से दोलन कर रहा है जब गोलक का विस्थापन, इसके अधिकतम मान से कम है उस स्थिति में इसका त्वरण सदिश सही रूप से दिखाया गया है
View Solutionसरल लोलक का कोणीय आयाम `theta_(0)` है। डोरी में अधिकतम तनाव होगा ?
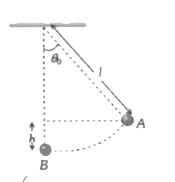
View SolutionL लम्बाई की रस्सी के एक सिरे पर पत्थर बाँधकर इसे ऊर्ध्वाधर वृत्त में घुमाया जाता है, रस्सी का दूसरा सिरा वृत्त के केन्द्र पर है। वृत्ताकार मार्ग के निम्नतम बिन्दु पर पत्थर का वेग u हो, तो उस स्थिति पर इसके वेग में परिवर्तन का परिमाण, जबकि रस्सी क्षैतिज अवस्था में है, होगा
View Solutionद्रव्यमान M का एक गोलक (दोलक), भारहीन डोरी (लम्बाई L) से लटकाया गया है। इसे बिन्दु 8 तक पहुंचने के लिए A पर वेग V तीक पर्याप्त होता है। तब कोण `theta` जिस पर गोलक की चाल, उसकी A पर चाल की आधी होगी, सन्तुष्ट होगा|
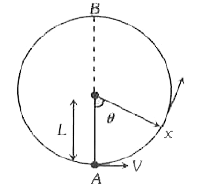
View Solutionचार व्यक्ति K,L,M तथा N प्रारम्भ में d लम्बाई की भुजा के वर्ग के चारों कोनों पर खड़े है। प्रत्येक व्यक्ति इस प्रकार चलना प्रारम्भ करता है कि K हमेशा L की ओर, L, M की ओर M,N की ओर तथा N,K की ओर मुँह किये हुये रहते हैं। चारों व्यक्ति कितने समय पश्चात् मिलेंगे|
View Solutionचित्रानुसार एक बिन्दु P घड़ी के चलने की विपरीत दिशा में वृत्तीय पथ पर गति करता है। 'P' की गति इस प्रकार है कि तय लम्बाई `(s=t^3 +5)` होती है, जहाँ S मीटर में तथा t सेकण्ड में है। पथ की त्रिज्या 20m है। अत: t=2s पर P का त्वरण लगभग है।
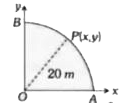
View Solutionएक तार के टुकड़े को मोड़ कर परवलय `y=kx^(2)` (y-अक्ष ऊर्ध्वाधर) का आकार दिया गया है। इस तार में m द्रव्यमान का एक मनका पड़ा है जो तार पर बिना घर्षण सरक सकता है। तार की स्थिर अवस्था में यह मनका परवलय के निम्नतम स्थान पर रहता है। अब तार को एकसमान त्वरण a से x-अक्ष के समान्तर चलाया जाता है। मनके की साम्यावस्था में, जहाँ वह तार की अपेक्षा स्थिर अवस्था में रह सकता है, उसकी y-अक्ष से दूरी होगी
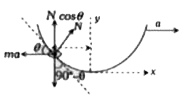
View Solutionघर्षणरहित टेबल के केन्द्र पर एक छोटा छिद्र बनाया गया है जिसमें से लम्बाई 2l की भारहीन डोरी प्रविष्ट की गई है। डोरी के दोनों सिरों से दो समान द्रव्यमान m की दो गेंद जोड़ी गई हैं। यह समंजन इस प्रकार का है कि आधी डोरी टेबल पर तथा आधी डोरी नीचे लटकी है। टेबल के ऊपर की गेंद को वृत्तीय पथ पर नियत चाल से घुमाया जाता है। गतिमान गेंद का अभिकेन्द्र त्वरण क्या होगा|
View Solutionचित्रानुसार वक्र पथ पर एक छोटा रोलर कॉस्टर बिन्दु A से u चाल के साथ गति प्रारम्भ करता है
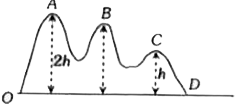
रोलर कॉस्टर तथा पथ के मध्य घर्षण नगण्य है तथा ये निरन्तर पथ के सम्पर्क में बना रहता है। पथ के बिन्दु D पर रोलर कॉस्टर की गति होगी|
View Solutionएक छोटा पिंड m एक द्रव्यमान-रहित धागे से जुड़ा है। धागे का दूसरा सिरा P पर बंधित हैं (चित्र देखिये।) पिंड x-y तल में एकसमान कोणीय चाल `omega` से वृत्तीय गति कर रहा है। वृत्त का केन्द्र O पर है। यदि O और P बिन्दुओं के सापेक्ष निकाले गये इस निकाय के कोणीय संवेग क्रमशः संवेग क्रमशः `vecL_O" और "vecL_P` है, तब
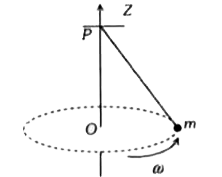
View Solutionयदि किसी समय पर किसी कण के x तथा y निर्देशांक क्रमशः `x=5t-2t^(2)" तथा "y=410t` है। (जहाँ x तथा y मीटर में और t सेकण्ड में है) तो t=2s पर उस कण का त्वरण होगा
View Solutionएक प्रसारी गोले की ताक्षणिक त्रिज्या R एवं द्रव्यमान M अचर होते है। प्रसार के दौरान इसका तात्क्षणिक घनत्व `rho` पूरे आयतन में एकसमान रहता है एवं आंशिक घनत्व की दर `(1/p (dp)/(dt))` अचर है। इस प्रसारी गोले के पृष्ठ पर एक बिन्दु का वेग v निम्न के समानुपाती होगा|
View Solutionएक त्रिविमीय निर्देशांक निकाय में गतिशील एक कण के स्थिति निर्देशांक निम्न हैं
`x=a cos omega t`
`y=a sin omega t`
तथा `z=a omega t`
इस कण की गति का मान होगा
View Solutionदो बन्दूकों A तथा B द्वारा आरम्भिक चालों क्रमश: 1km/s तथा 2km/s से गोली चलायी जा सकती है। क्षैतिज भूमि के किसी बिन्दु से सभी सम्भव दिशाओं में इनकों चलाया जाता है। दोनों बन्दूकों द्वारा दांगी गई गोलियों से भूमि पर छादित अधिकतम क्षेत्रफलों का अनुपात है।
View Solutiont= 0 पर क्षैतिज से `60^@` के कोण पर `10ms^(-1)` के वेग से एक पिण्ड को प्रक्षेपित करते है। t=1s पर प्रक्षेप पथ की वक्रता त्रिज्या R है। वायु प्रतिरोध को नगण्य मानकर तथा गुरूत्वीय त्वरण `g=10ms^(-2)` लेकर R का मान है
View Solutionएक कण एक वृत्ताकार पथ पर `10ms^(-1)` की नियत गति से चल रहा है। जब यह कण वृत्त के केन्द्र के परितः `60^@` चलता है तो इसके वेग में हुये परिवर्तन का परिमाण होगा
View Solutionएक 60m लम्बी यात्री गाड़ी 80 km/hr की गति से चल रही है। 120m लम्बाई की और एक माल गाड़ी 30km/hr से चल रही है। ऐसे समयों का अनुपात जो यात्री गाड़ी को मालगाड़ी को पार करने में लगेंगे जब गाड़ियाँ एक ही दिशा में जा रही हैं, और (ii) गाड़ियों विरोधी दिशाओं में जा रही हैं, होगा
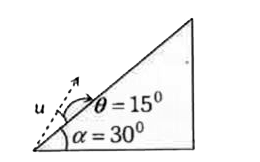
View Solutionएक समतल क्षैतिज से `alpha=30^@` का कोण बनता है एक कण को इस समतल के आधार से गति `u= 2ms^(-1)` से समतल से `theta=15^@` के कोण पर चित्रानुसार प्रक्षेपित किया जाता है। उस बिन्दु, जहाँ कण समतल पर गिरता है, की आधार पर गिरता है, की आधार से दूरी का सन्निकट मान होगा| (g=10ms^(-2)` लीजिये)
View Solutionकिसी प्रक्षेप्य के प्रक्षेप-पथ को, भू पृष्ठ पर `y=2x-9x^(2)` से निरूपित किया जाता है। यदि, इसे `v_(0)` चाल द्वारा `theta_(0)` कोण पर प्रमोचित किया गया होता तो, `(g=10ms^(-2))`
View Solutionकिसी स्थिर तोप से एक गोला, प्रारंभिक चाल u से ऐसे कोण पर, दागा जाता है कि गोला भूतल पर अपने लक्ष्य पर लगता है। लक्ष्य की तोप से R दूरी है। यदि गोले द्वारा लक्ष्य पर लगने के दो संभव मार्ग हैं, और इनमें लगे समय क्रमशः `t_(1)` तथा `t_(2)` हैं तो, गुणनफल `t_(1)t_(2)` होगा-
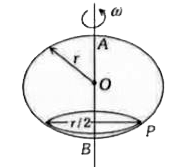
View Solution`2pir` लम्बाई के एक घर्षण रहित तार को वृत्त बनाकर ऊर्ध्वाधर समतल में रखा है। एक मणिका (bead) इस तार पर फिसलती है। वृत्त को एक ऊर्ध्वाधर अक्ष AB के परितः चित्रानुसार कोणीय वेग `omega` से घुमाया जाता है तो वृत्त के सापेक्ष मणिका चित्रानुसार बिन्दु P पर स्थिर पायी जाती है। `omega^(2)` का मान होगा
View Solutionदो कणों को एक ही बिन्दु से एक ही चाल u से प्रक्षेपित किया जाता है जिससे उनकी परास R बराबर हैं किन्तु अधिकतम ऊँचाइयाँ `h_(1)` तथा `h_2` भिन्न हैं। निम्न में सत्य कथन चुनिये
View Solution10kg द्रव्यमान का कोई गुटका 1m त्रिज्या को किसी खोखले बेलनाकार ड्रग की भीतरी दीवार के सम्पर्क में है। भीतरी दीवार और गुटके के बीच घर्षण गुणांक 0.1 है। जब बेलन ऊर्ध्वाधर हे और अपने अक्ष के परित घूर्णन कर रहा है, तो गुटके को स्थिर रखने के लिए आवश्यक निम्नतम कागाथा बा होगा `(g=10m//s^(2))`
View Solutionकिसी पतले तार से जुड़े द्रव्यमान M को किसी ऊर्ध्वाधर वृत्त में तीव्रता से घुमाया जा रहा है। इस तार के टूटने की अधिक संभावना तब है जब
View Solution`r_(A)" और "r_(B)` त्रिज्याओं के संकेन्द्री वृत्तों पर दो कण A और B क्रमशः `v_(A)" और "v_(B)` वेगों से एकसमान वृत्तीय गति कर रहे हैं। इनके घूर्णन का आवर्तकाल समान है। A और B की कोणीय चालों का अनुपात होगा।
View Solutionजब क्षैतिज से `60^@` कोण पर रखे किसी लम्बे चिकने आनत तल की तली से किसी पिण्ड पर शॉट लगाया जाता है, तो वह तल के अनुदिश `x_1` दूरी चल सकता है। परन्तु जब झुकाव को घटाकर `30^@` कर दिया जाता है तथा इसी पिण्ड पर समान वेग से शॉट लगाया जाता है, तब वह `x_2` दूरी चल सकता हैं। तब `x_(1) : x_(2)` होगा|
View Solution
Critical Thinking (Objective Questions) questions and complete solutions for chapter द्वि-विमीय गति of ERRORLESS PHYSICS (HINDI) of Class 12