Complete Solutions to Ordinary thinking (गति का द्वितीय नियम) of chapter न्यूटन के गति के नियम of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | न्यूटन के गति के नियम |
| ERRORLESS HINDI | Ordinary thinking (गति का द्वितीय नियम) |
| Number Of Questions | 52 |
| Academic Year | 2023-24 |
एक 5 ग्राम द्रव्यमान की गोली, `100m//sec` के वेग से, एक लकड़ी के गुटके में 6 cm तक धंस जाती है। तब गोली द्वारा गुटके पर आरोपित औसत बल है :
View Solution`0.4kg` द्रव्यमान की एक वस्तु `t=0` पर `10m//s` की गति से धनात्मक x-अक्ष के मूलबिन्दु से `F=8N` नियत बल के साथ ऋणात्मक x-अक्ष की ओर जाती है। 25 सेकण्ड पश्चात वस्तु की स्थिति की गणना कीजिए।
View Solution`100m` दूरी तय करने में `20kg` द्रव्यमान के पिण्ड का वेग `20m//s` से घटकर `5m//s` हो जाता है। पिण्ड पर बल होगा :
View Solutionद्रव्यमान m की एक गेंद v चाल से एक दीवार से लंबवत् टकराती है तथा उसी प्रकार लंबवत् वापस लौटती है, यदि दीवार के साथ गेंद का संपर्क समय t हो तब गेंद द्वारा दीवार पर आरोपित बल होगा
View Solutionएक `0.2` कि . ग्रा . द्रव्यमान की गेंद को हाथ की सहायता से उर्ध्वाधर ऊपर की ओर फेंका जाता है। यदि हाथ `0.2` मी . चलता हो ओर हाथ से लगाये गये बल से गेंद `2` मी . की ऊँचाई तक जाती है, तो हाथ द्वारा लगाये गये बल का परिणाम होगा ( `g=10` मी/से`"^(2)` लेने पर )
View Solutionवास्तव में बल का समीकरण है
View Solution`4` किग्रा द्रव्यमान के एक पिण्ड को नियत बल द्वारा त्वरित किये जाने पर वह प्रथम सेकण्ड में 5 मी दूरी तथा तीसरे सेकण्ड में 3 मी दूरी तय करता है। पिण्ड पर क्रियाशील बल होगा
View Solution`0.05` kg द्रव्यमान का एक पिण्ड `9.5ms^(-2)` के त्वरण से गिरता है। वायु द्वारा पिण्ड पर आरोपित विरोधी बल है `g=9.8ms^(-2)`
View Solutionएक 10kg का पिण्ड रस्सी द्वारा लटकाया गया है, रस्सी की त्रोटन सामथर्य 30kg wt है। इसे 10m की ऊँचाई तक कितने न्यूनतम समय में उठाया जा सकता है। (g=10N/kg)
View Solutionएक समतल क्षैतिज सतह पर m द्रव्यमान का पिण्ड विराम में है। m/3 द्रव्यमान की समरूप डोरी के एक सिरे से द्रव्यमान जोड़ा गया है, जिसे दूसरे सिरे पर बल F द्वारा क्षैतिज दिशा में खींचा जाता है। तब डोरी के मध्य में तनाव होगा
View Solutionएक कण x-y तल में, एक बल के प्रभाव में इस प्रकार गति करता है कि उसका रेखीय संवेग निम्न प्रकार से दिया जाता है `vecp(t)=A[haticos(kt)-hatjsin(kt)]` जहाँ A और k नियतांक है, तब बल तथा संवेग के मध्य कोण है
View Solutionएक निर्देश तन्त्र पृथ्वी से जुड़ा हुआ है
View Solutionm द्रव्यमान का एक बैलून (गुब्बारा) a त्वरण से नीचे उतर रहा है (जहाँ algg)। इसमें से कितने द्रव्यमान का पदार्थ हटा दिया जाय कि यह a त्वरण से ऊपर की ओर जाने लगे
View Solutionएक व्यक्ति का द्रव्यमान `60 kg` है। वह `940 kg` द्रव्यमान के लिफ्ट में खड़ा होकर लिफ्ट का बटन दबाता है, जिससे लिफ्ट `1.0m//s^(2)` के त्वरण से ऊपर की ओर गति करती है। यदि g का मान `10ms^(-2)` हो, तो उस केबल में, जिससे लिफ्ट लटकी रहती है, तनाव होगा
View Solutionएक लिफ्ट नीचे की ओर त्वरण a से गतिमान है। एक व्यक्ति लिफ्ट के अन्दर एक गेंद को गिराता है। लिफ्ट के अन्दर उपस्थित व्यक्ति एवं जमीन पर खड़े व्यक्ति के सापेक्ष गेंद के त्वरण क्रमश : है
View Solutionm द्रव्यमान का एक गुटका `theta` झुकाव वाले चिकने तल पर रखा है। संपूर्ण निकाय को इस प्रकार क्षैतिजत : त्वरित किया जाता है जिससे गुटका तल पर न फिसले। तल द्वारा गुटके पर लगाया गया बल होगा (g गुरुत्वीय त्वरण है )
View Solutionएक लिफ्ट पुर की ओर जा रही है। लिफ्ट तथा लिफ्ट में उपस्थित यात्री का संयुक्त द्रव्यमान 1500 किग्रा है। लिफ्ट की चाल में परिवर्तन दर्शाये गये ग्राफ में प्रदर्शित है | t=11 सैकण्ड पर लिफ्ट खींचने में प्रयुक्त रस्सी में तनाव होगा
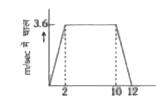
View Solutionउपरोक्त प्रश्न में, लिफ्ट यात्री को किस ऊँचाई तक ले जा सकती है
View Solution`5` किग्रा द्रव्यमान की एक वस्तु को किसी नतसमतल पर रखी हुई स्प्रिंग तुला से लटकाया गया है, जैसा कि चित्र में प्रदर्शित है। स्प्रिंग तुला का पाठ्यांक होगा

View Solution3 किग्रा. तथा 5 किग्रा. के दो पिण्ड विरामावस्था है यदि इन पर समान बल लगाया जाये तो इनके द्वारा समान वेग प्राप्त करने में लगे समयों का अनुपात होगा
View Solutionसामान्य आकाशीय प्रयोगों के लिए, निम्नलिखित तथ्यों में प्रेक्षक एक जड़त्वीय तन्त्र है
View Solutionएक व्यक्ति एक लिफ्ट में खड़ा है। किस स्थिति में उसका भार वास्तविक भार से कम होगा जब
View Solution`0.3` किग्रा द्रव्यमान की किसी वस्तु पर बल `F=-kx` कार्यरत है, जहाँ `k=15N/m` है। वस्तु का प्रारंभिक त्वरण क्या होगा, जब इसे मुलबिन्दु से `20` सेमी दूरस्थ बिन्दु से छोड़ा जाता है
View Solutionनिम्न में सै कौन - सी राशि, जो विभिन्न जड़त्वीय निर्देश तंत्रों से मापने पर समान रहती है
View Solution`2xx10^(7)` कि .ग्रा . का एक जहाज है। `25xx10^(5)` N का बल लगाने पर `25` मी. विस्थापित हो जाता है, तो इस विस्थापन में जहाज द्वारा प्राप्त चाल होगी
View Solutionमानव ह्रदय रक्त को नियत वेग `vms^(-1)` से M kg `s^(-1)` की दर पर संचालित करता है। इसके लिये आवश्यक बल (N में) होगा
View SolutionM द्रव्यमान की एक ठोस चकती को वायु में क्षैतिजतः ऊध्वार्धर ऊपर की ओर `6` मी/ सै के वेग से प्रति सेकेंड फेंके जा रहे `40` पत्थरों द्वारा संतुलित किया गया है। यदि प्रत्येक पत्थर का द्रव्यमान `0.05` किग्रा हो, तो चकती का द्रव्यमान है `(g=10m//s^(2))`
View Solutionएक डोरी से बँधे गोले को ऊपर की दिशा में त्वरित किया जाता है। गोले के भार के चार गुना सामथर्य पर डोरी टूट जाएगी। तब गोले के लिए अधिकतम त्वरण क्या होगा, जिससे घुमाने पर डोरी न टूटे
View Solution`1000` kg द्रव्यमान का एक सैनिक वाहन 10 m/s के वेग से गतिमान है और इस पर इंजिन द्वारा आगे की दिशा में `1000` N का बल एवं घर्षण के कारण `500` N का अवमंदक बल कार्यरत् है। `10` sec प्रश्चात इसका वेग होगा
View Solutionएक व्यक्ति लिफ्ट के अन्दर भार मापने की मशीन पर खड़ा होकर अपने भार का मापन करता है। जब लिफ्ट विराम में होती है, तब मशीन `55` kg भार दर्शाती है। जब लिफ्ट `10 km//hr` की नियत चाल से ऊपर गति करती है, तब वह अपना भार पुनः मापता है, जो होगा
View Solutionजब किसी गतिशील वस्तु की चाल को दोगुना किया जाता है तो
View Solution`5` ग्राम द्रव्यमान की किसी वस्तु पर `100` डाइन का बल `10` सैकण्ड तक लगाया जाता है। वस्तु का वेग होगा
View Solution`5kg` द्रव्यमान की चाल `0.2sec` में `65cm//s` से घटाकर `15cm//s` करने के लिए इस पर कार्यरत् अवरोधी बल होना चाहिए
View Solutionएक लड़का जिसकी संहति 40 किलोग्राम है एक ऐलीवेटर में खड़ा है। इस लड़के के पैरों द्वारा अनुभव किया गया बल सर्वाधिक होगा जबकि ऐलीवेटर `(g=9.8 मी/ सैकण्ड^(2))`
View Solution`5kg` द्रव्यमान का एक टुकड़ा `1.5m//s` के वेग से क्षैतिज दिशा में गति कर रहा है। `5` न्यूटन का एक लम्बवत् बल इस पर `4` sec तक कार्य करता है तो उस बिन्दु से, जहाँ से बल कार्यरत् होता है, गुटके की दूरी होगी
View Solutionएक व्यक्ति का लिफ्ट में भार, जब लिफ्ट स्थिर है और जब वह एकसमान त्वरण 'a' से नीचे जाती है, का अनुपात `3:2` है तो 'a' का मान है (g=पृथ्वी का गुरुत्वीय त्वरण )
View Solutionयदि `20` g द्रव्यमान की एक गोली `250` m/s की चाल से लकड़ी के अन्दर `12` cm तक धंस जाती है, तो इसको विरामावस्था तक लाने में आवश्यक औसत बल है
View Solutionएक गोली किसी लक्ष्य पर चलाई जाती है, तो लक्ष्य में 30 सेमी धसने के बाद उसका वेग प्राम्भिक वेग का आधा हो जाता है तो विरामावस्था में आने से पहले वह कितनी और धसेगी
View Solution`5` किग्रा द्रव्यमान की एक वस्तु मूल बिन्दु से प्रारभिक वेग `vecu=30hati+40hatj` मी / सै से गति प्रांरभ करती है। यदि वस्तु पर एक नियत बल `vecF=-(hati+5hatj)N` लगाया जाए, तो वह समय जिसमें वेग का y घटक शून्य हो जायेगा, होगा
View Solutionएक स्प्रिंग तुला लिफ्ट की छत से जुडी है। एक व्यक्ति अपना थैला इस स्प्रिंग पर टांग देता है, जब लिफ्ट स्थिर है तो यह `49` N का पाठ्यांक देती है। यदि लिफ्ट नीचे की ओर `5m//s^(2)` के त्वरण से गतिमान हो जाये तो स्प्रिंग तुला का पाठ्यांक होगा
View Solutionएक स्थिर लिफ्ट में एक आदमी पानी से भरी एक बाल्टी लिये खड़ा है जिसकी पेंदी में एक छेद है। इस छेद से पानी के बहने की दर `R_(0)` है। यदि लिफ्ट ऊपर और नीचे एक समान त्वरण से चलने लगे और तब पानी के बहने की दर क्रमश : `R_(u)` और `R_(d)` हो, तो
View Solutionस्प्रिंग तुला से लटका हुआ पिण्ड तथा एक व्यक्ति ऊपर की ओर उठते हुए हवाई जहाज में बैठे है। तब स्प्रिंग तुला द्वारा दर्शाया जाने वाला पिण्ड का भार
View Solutionएक गतिमान कार की छत से एक गोले को डोरी की सहायता से लटकाया गया है। यदि कार क्षैतिज त्वरण a से गतिमान हो तो डोरी ऊर्ध्वाधर से कितना कोण बनाएगी
View Solution`20` kg का एक बन्दर एक ऊर्ध्वाधर रस्सी को पकड़े हुए है। यदि रस्सी पर `25` kg द्रव्यमान लटकाया जाये तो रस्सी नहीं टूटती है परन्तु यदि इस पर `25` kg से ज्यादा द्रव्यमान लटकाया जाये तो यह टूट जायेगी। वह अधिकतम त्वरण क्या होगा जिससे बन्दर रस्सी पर ऊपर की ओर चढ़ सकें। `(g=10m//s^(2))`
View Solution`10` N का एक बल `20` kg द्रव्यमान की एक वस्तु पर `1` sec तक कार्य करता है। इसके संवेग में परिवर्तन है
View Solutionएक विमीय गति करती हुई वस्तु का रेखीय संवेग p, समय के साथ समीकरण `p=a+bt^(2)` के अनुसार परिवर्तित होता है, जहाँ a तथा b धनात्मक नियतांक है। वस्तु पर लगने वाला परिणामी बल होगा
View Solution`1.0` kg द्रव्यमान की एक वस्तु `10m//s^(2)` के त्वरण से गिर रही है। इसका आभासी भार होगा `(g=10m//s^(2))`
View Solutionक्षैतिजतः खिंचे हुए जाल का एक भाग चित्र में प्रदर्शित है। भाग AB को `10` N के बल से खींचा जाता है। BC तथा BF भागों में तनावों का मान है :
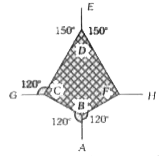
View Solutionएक क्रिकेट खिलाड़ी `20` मी / सै की दर से गतिशील `0.15` kg की गेंद को पकड़ता है। यदि गेंद पकड़ने में लगा समय `0.1` सैकण्ड हो, तो गेंद द्वारा खिलाड़ी के हाथों पर लगाया गया बल होगा
View Solutionn छोटी गेंदे, जिनमें प्रत्येक का द्रव्यमान m है, किसी सतह से प्रत्यास्थतः u वेग से टकराती है। सतह पर लगने वाले बल का मान होगा
View Solutionकिसी द्रव्यमान पर लगने वाला बल `vecF=6hati-8hatj+10hatk` है तथा उत्पन्न त्वरण `1m//s^(2)` है। वस्तु का द्रव्यमान होगा
View Solutionकोई कण xy- समतल में बल `vecF` के प्रभाव में इस प्रकार गति करता है कि इसके रेखीय संवेग `vecP` के घटक किसी समय t पर `p_(x)=2cost` तथा `p_(y)=2sint` है। समय t पर बल `vecF` तथा संवेग `vecp` के बीच का कोण है
View Solution
Ordinary thinking (गति का द्वितीय नियम) questions and complete solutions for chapter न्यूटन के गति के नियम of ERRORLESS PHYSICS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 PHYSICS न्यूटन के गति के नियम
- Assertion & Reason
- Critical thinking
- Graphical Question
- Jee section (Comperhension Type Question )
- Jee section (Integer type Question)
- Jee section (Jee advance 2018)
- Jee section (Matrix match type Question)
- Jee section (more than one correct answer )
- Jee section (Reasoning type Question )
- Ordinary thinking (गति का तृतीय नियम )
- Ordinary thinking (गति का द्वितीय नियम)
- Ordinary thinking (गति का प्रथम नियम)
- Ordinary thinking (बलों की साम्यावस्था )
- Ordinary thinking (रेखीय संवेग का संरक्षण तथा आवेग)
- Ordinary thinking (संलग्न पिण्डों की गति )
- Self evaluation