Complete Solutions to Critical thinking of chapter प्रत्यास्थता of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | प्रत्यास्थता |
| ERRORLESS HINDI | Critical thinking |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
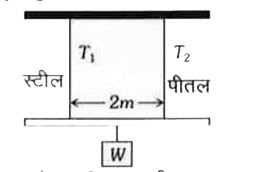
`2m` लम्बाई की भारहीन छड़ को छत से दो ऊर्ध्वाधर तारों द्वारा क्षैतिज स्तिथि में लटकाया गया है। एक भार `W` को चित्रानुसार भारहीन छड़ से लटकाया गया है । छड़ को लटकने वाले स्टील के तार के अनुप्रस्थ काट का क्षेत्रफल `A_(1)=0.1cm^(2)` तथा पीतल के तार के अनुप्रस्थ काट का क्षेत्रफल `A_(2)=0.2cm^(2)` है। समान प्रतिबल के लिए तारो में `T_(1)//T_(2)=`
View Solutionकिसी तार को तोड़ने के लिये `10^(6)N//m^(2)` बल की आवश्यकता होती है। यदि पदार्थ का घनत्व `3xx10^(3)kg//m^(3)` है , तो उस तार की लम्बाई क्या होनी चाहिए जो अपने ही भार से ही टूट जायेगा।
View Solutionदो विभिन्न पदार्थो वाली छड़ों के रेखीय प्रसार गुणांक `alpha_(1)` व `alpha_(2)` तथा यंग गुणांक क्रमशः `Y_(1)` व `Y_(2)` है, इन्हे दो दृढ स्थिर दीवारों के बीच कसा गया हैं । छड़ों को इस प्रकार गर्म किया जाता हैं कि प्रत्येक के ताप में समान वृद्धि होती हैं । छड़े झुकती नहीं हैं। यदि `alpha_(1) : alpha_(2)=2 : 3` एवं छड़ों के तापीय प्रतिबल बराबर हैं तो `Y_(1) : Y_(2)` का मान होगा
View Solutionस्टील के दो यंग प्रत्यास्थता गुणांक , पीतल से दो गुना होते है। एक ही लम्बाई तथा एक ही अनुप्रस्थ काट के दो तारों ,(एक स्टील का तथा एक पीतल का ) को एक ही छत से लटकाया जाता है । यदि हम चाहते है कि दोनों तारों को निचले सिरे एक ही तल पर है तो स्टील तथा पीतल के तारों से लटकाये जाने वाले भारों का अनुपात होना चाहिए
View Solutionएक धातु की छड़ ,जिसकी लम्बाई 'L' अनुप्रस्थ काट का क्षेत्रफल 'A' यंग प्रत्यास्थता गुणांक 'Y' तथा रेखीये प्रसार गुणांक `'alpha'`है। , को `'t'^(@)C` तक गर्म किया जाता है । गर्मं करने पर धातु द्वारा किया गया कार्य हो सकता है
View Solution`m` द्रव्यमान का कण एक बल `F` के प्रभाव में है। यह बल `F=-kx+F_(0)` द्वारा दिया जाता है। यहाँ x` विस्थापन जबकि k`तथा `F_(0)` नियंताक है। कण को साम्यावस्था से विस्थापित करने पर यह कम्पन करेगा
View Solutionस्प्रिंग की लम्बाई में `x` वृद्धि के लिये आरोपित बल `F=(-5x-16x^(3))N` है। स्प्रिंग की लम्बाई में `0.1` मी से `0.2` मीटर तक की वृद्धि में किया गया कार्य होगा
View Solutionएक छात्र `2`मी. लम्बाई के तार का यंग गुणांक ज्ञात करने के लिये सर्ल विधि का प्रयोग करता है। एक विशेष प्रेक्षण में `1` किग्रा भार के संगत लम्बाई में `0.8mm` वृद्धि को `+-0.05mm` अनिश्चितता के साथ मापता है। छात्र तार का व्यास `0.4mm` को भी `+-0.01` अनिश्चितता के साथ मापता है। यदि `g=9.8"मी"//"से"^(2)` लिया जाये प्रेक्षण द्वारा यंग गुणक प्राप्त होगा
View Solutionएक पलड़े में कुछ भार रख कर इसे हल्की स्प्रिंग से लटकाया गया। जब इसे साम्यावस्था से विस्थापित किया जाता है , तो द्रव्यमान स्प्रिंग निकाय `0.6` सैकण्ड के आवर्तकाल के साथ दोलन करता है। जब कुछ और भार पलड़े में रखा जाये तो आवर्तकाल `0.7` सैकण्ड हो जाता है। अतिरिक्त भार के कारण स्प्रिंग से प्रसार होगा लगभग
View Solutionचित्रनुसार स्टील तथा पीतल के तार के लम्बाइयों त्रिज्याओं तथा यंग गुणाकों का अनुपात क्रमश : a,b तथा c है तब पीतल तथा स्टील के तार के मध्य, लम्बाई में वृद्धि का अनुपात होगा
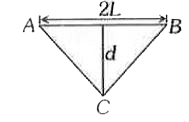
View Solutionएक `2L` लम्बाई एवं `r` त्रिज्या का तार बिना किसी तनाव के `A` तथा `B` के बीच तना है। यदि तार का यंग प्रत्यास्थता गुणांक Y हो तथा उसे ACB की भाँति ताना जाए, तो तार में तनाव होगा
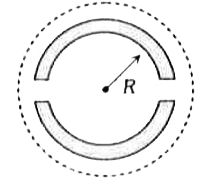
View Solutionत्रिज्या R का एक लकड़ी का पहिया दो अर्द्धवृतीय भागो से बनाया गया है (चित्र देखे) लम्बाई L और अनुप्रस्थ परिच्छेद क्षेत्रफल S की एक धातु की पट्टी से बने एक वलय द्वारा दोनों भागो को पकड़ कर रखा गया है L का मान `2piR` से कुछ कम है। वलय को पहिये पर चढ़ने के लिये, इसे गर्म किया जाता है जिससे की इसके तापमान में `DeltaT` की वृद्धि हो और यह पहिये के ऊपर बस चढ़ जाए। जब यह वातावरण के तापमान तक ठंडा होता है , यह अर्द्धवृतीय भागो को एक साथ दबाता है। यदि धातु का रैखिक प्रसार गुणांक `alpha` और यंग प्रत्यास्थता गुणांक `Y` है तब एक भाग दूसरे भाग पर लगाया गया बल है
View Solutionलम्बाई `L` द्रव्यमान `M` और अनुप्रस्थ परिछेद क्षेत्रफल `A` वाले एक समान बेलन को इसकी लम्बाई ऊर्ध्वाधर रखते हुए एक द्रव्यमानविहीन कमानी द्वारा एक नियत बिन्दु से इस प्रकार लटकाया गया है की साम्यावस्था स्थिति में इसका आधा भाग घनत्व `sigma` के द्रव में डूबा रहे। जब यह साम्यावस्था में है, तब कमानी में विस्तार `x_(0)` है
View Solutionअसत्य कथन चुनिए
View Solutionरेखीय प्रसार गुणक `alpha//^(@)C` वाली धातु से बनी लम्बाई L तथा एक समान अनुप्रस्थ काट के क्षेत्रफल A की एक छड़ को कक्ष तापमान पर रखा गया है। जब एक बाहा संदाबी बल F को इसके प्रत्येक सिरों पर लगते है तो `DeltaTK` की तापमान वृद्धि होने पर, छड़ की लम्बाई में कोई परिवर्तन नहीं पाया जाता है। इस धातु का यांग प्रत्यास्थता गुणांक, Y होगा
View Solutionसर्ल उपकरण के एक प्रयोग में `M kg` द्रव्यमान के एक भार को `2m` लम्बाई तथा `1.0mm` त्रिज्या के एक स्टील के तार से लटकाते है। तार की लम्बाई में `4.0mm` की वृद्धि होती है। अब भार को आपेक्षिक घनत्व `2` वाले द्रव में डुबो देते है। भार के पदार्थ का आपेक्षिक घनत्व `8` है। तार की लम्बाई में वृद्धि का नया मान होगा
View Solutionएक बालक का गुलेल `42cm` लम्बी और `6mm` अनुप्रस्थ काट के व्यास की रबड़ की डोरी का बना है , जिसका द्रव्यमान नगण्य है। बालक `0.02kg` भार का एक पत्थर इस पर रखता है और डोरी को एक नियत बल से `20cm` द्वारा तानित करता है। जब इसे छोड़ता है तब पत्थर `20ms^(-1)` के वेग से जाता है। तानित होने पर डोरी के अनुप्रस्थ काट में परिवर्तन नगण्य है रबड़ का यंग प्रत्यास्थता गुणांक का निकटतम मान है
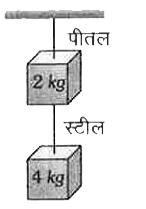
View Solution`4kg` के भार को वहन करते हुए एक `2.0mm` त्रिज्या के स्टील के एक तार को छत से लटकाया गया है। दिया है `g=3.1pims^(-2)` । तार में उत्पन्न तन्य प्रतिबल का मान क्या होगा
View Solutionदो तारो A तथा B के यंग प्रत्यास्थता गुणाको का अनुपात `7 : 4` है। तार A की लम्बाई `2m` तथा त्रिज्या `R` है। तार B की लम्बाई `1.5m` तथा त्रिज्या `2mm` है। यदि इन दोनों तारो की लम्बाई में वृद्धि एक दिये गये भार के कारण, बराबर है तो R का सन्निकट मान होगा
View Solutionपीतल की प्रत्यास्थता सीमा `379Mpa` है। `400N` बल को बिना प्रत्यास्थता सीमा पर किये सह सकने वाली पीतल की छड़ का न्यूनतम व्यास क्या होगा
View Solutionएक प्रयोग में पीतल तथा स्टील के दो तारो का प्रयोग किया गया है जिनमे प्रत्येक की लम्बाई `1m` तथा अनुप्रस्थ काट का क्षेत्रफल `1mm^(2)` है। इन तरो को श्रेणीक्रम में जोड़ते है तथा संयुक्त तार के एक सिरे को दृंढ स्तम्भ से जोड़ते है एवं दूसरे सिरे को खींचा जाता है `0.2mm` की कुल वृद्धि के लिये प्रतिबल का मान होगा (दिया है , स्टील तथा पीतल के यंग प्रत्यास्थता गुणांक, क्रमश : `120xx10^(9)N//m^(2)` तथा `60xx10^(9)N//m^(2)`)
View Solutionजब द्रव्यमान M के किसी गुटके को L लम्बाई के किसी तार से निलंबित किया जाता है, तो तार की लम्बाई `(L+I)` हो जाती है। विस्तारित तार में संचित प्रत्यास्थ स्थितिज ऊर्जा है
View Solution
Critical thinking questions and complete solutions for chapter प्रत्यास्थता of ERRORLESS PHYSICS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 PHYSICS प्रत्यास्थता
- Assertion & Reason
- Critical thinking
- Graphical Questions
- Jee (Advanced) 2018
- Jee Section(Comprehension type questions)
- Jee Section(Integer type questions)
- Jee Section(Matrix match type questions)
- Jee Section(More than one correct answers)
- Jee Section(Reasoning type questions)
- Ordinary thinking
- Self Evaluation test