Complete Solutions to Ordinary Thinking(तरल प्रवाह ) of chapter तरल यांत्रिकि of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | तरल यांत्रिकि |
| ERRORLESS HINDI | Ordinary Thinking(तरल प्रवाह ) |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
निम्न में से किस स्थिति में नली में द्रव का प्रवाह अधिक रेखीय होगा
View Solutionकोई इंजन एक होज़पाइप से निरंतर जल को पम्प कर रहा है। होजपाइप से जल वेग v से निकलता हैं और जल की धारा का प्रति मात्रक l लंबाई द्रव्यमान m हैं। जल को गतिज ऊर्जा दिये जाने की दर क्या होगी
View Solutionकिसी स्प्रे पम्प की बेलनाकार नली की त्रिज्या R है। इस नली के सिरे पर n सूक्ष्म छिद्र हैं, जिनमें प्रत्येक की त्रिज्या `r` है। यदि नली में द्रव की चाल V है तो इन छिद्रों से बाहर निकालते हुए अब की चाल होगी
View Solutionअसमान अनुप्रस्थ परिच्छेद की नलिका की M और N पर त्रिज्या क्रमशः 0.1 m तथा 0.05m है। धारा रेखीय प्रवाह में द्रव प्रवाह की दर होगी

View Solutionशीर्ष भाग से कटे शंकू के आकार की नली में से द्रव प्रवाहित किया जाता है। निम्न में से सत्य कथन चुनिए
View Solutionएक जल विद्युत शक्ति केन्द्र में बाँध की ऊँचाई 10 मी. है। 1 MW की विद्युत शक्ति उत्पन्न करने के लिए टर्बाइन के ब्लेड पर प्रति सेकण्ड गिरने वाले जल का द्रव्यमान (किग्रा में) होगा
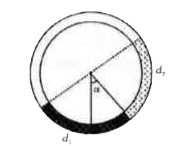
View Solutionएक वृत्ताकार नली ऊर्ध्वाधर तल में है। दो द्रव, जो एक दूसरे से मिश्रित नहीं होते तथा जिनका घनत्व `d_(1)` एवं `d_(2)` हैं, नली में भरे गये हैं। प्रत्येक द्रव केन्द्र पर 90° का कोण अंतरित करता हैं। उनके अंत पृष्ठ को जोड़ने वाली त्रिज्या ऊर्ध्वाधर से `alpha` कोण बनाती हैं। अनुपात `d_(1)//d_(2)` है
View Solutionघनत्व p के द्रव की आठ बूंदें (प्रत्येक की त्रिज्या a) वायु में नियत वेग 3.75 cm`s^(-1)` से गिर रही हैं। जब आठ बूंदें संयुक्त होकर एक बूंद बनाती है। तब नई बूंद का सीमान्त वेग होगा
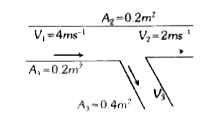
View Solutionचित्र में वेग `V_(3)` होगा
View Solutionएक बड़ा पात्र 'h' ऊँचाई तक जल से भरा है। उसके पेंदे में छेद करके खाली करने पर, जल स्तर h से `h/2` व `h/2` से 0 होने में लगे समयों का अनुपात होगा
View Solution20 मीटर ऊँचा बेलनाकार पात्र पूर्णतः जल से भरा है। पात्र के तल के एकदम समीप दीवार में छिद्र से निकलने वाले द्रव का बहिःस्राव वेग (m/s) होगा
View Solutionजल से भरे पात्र के तली में छिद्र है। तली पर कुल दाब `3 atm (1 atm = 10^(5)N//m^(2))` है। छिद्र से निकलने वाले जल का वेग होगा
View Solutionआन्तरिक व्यास `8xx10^(-3)m`m के नल से जल निरंतर प्रवाहित हो रहा है। नल से निकलते समय जल का वेग `0.4ms^(-1)` है। जल धारा का नल से `2xx10^(-1)`m नीचे व्यास होगा
View Solutionएक नदी की गहराई 10 m है, इसके पृष्ठ की पर्त का वेग `5 ms^(-1)` है। पृष्ठ की पर्त तथा तली की पर्त का अपरूपण प्रतिबल है (जल का श्यानता गुणांक `eta = 10^(-3)` SI मात्रक)
View Solutionएक वर्गाकार प्लेट (प्रत्येक भुजा 0.1 m) किसी दूसरी वर्गाकार प्लेट के समांतर 0.1 m/s के वेग से गति करती है। दोनों प्लेटें जल में डुबी हुयी हैं। यदि श्यानता गुणांक 0.01 पॉइज व श्यान बल 0.002 N हो तो प्लेटों के मध्य दूरी मीटर में होगी
View Solutionr त्रिज्या की गोलाकार गेंद, श्यानता वाले द्रव में वैग से गिर रही है। गेंद पर कार्यरत मंदक श्यान बल
View Solutionएक बहुत संकीर्ण नली से जल प्रवाहित हो रहा है। तब जल का वेग जिससे कम प्रवाह पर, प्रवाह धारा रेखीय होता है, जाना जायेगा
View Solutionवायु में दक्षिणावर्त दिशा में चक्रण गति से गतिमान क्रिकेट बॉल के लिये सत्य कथन का चयन कीजिये
S1 वायु का धारा रेखीय प्रभाव बॉल के परितः सममित होता है।
S2 बॉल के ऊपर वायु का वेग, बॉल के नीचे की अपेक्षा अधिक होता है।
S3 बॉल के ऊपर वायु का वेग, बॉल के नीचे की अपेक्षा कम होता है।
S4 बॉल पर परिणामी बल ऊपर की दिशा में होता है।
View Solutionबरनॉली सिद्धांत की क्रियाविधि व्याख्या संबंधित नहीं है
View Solutionकिसी r त्रिज्या व l लम्बाई की केशनली के सिरों पर दाबान्तर P है व इससे प्रति सैकण्ड प्रवाहित द्रव का आयतन V है। यह नली समान लम्बाई व आधी त्रिज्या की किसी अन्य नली के साथ श्रेणी क्रम में जोड़ी जाती है। तो प्रति सैकण्ड प्रवाहित द्रव का आयतन होगा। (यदि पूरे श्रेणीक्रम के सिरों पर दावांतर P है)
View Solutionएक समान क्षैतिज केशनली से एक द्रव प्रवाहित हो रहा है। नली के सिरों पर दाबांतर P है। किस दाब पर नली की त्रिज्या तथा लम्बाई दुगुनी करने पर, प्रवाह वेग भी दो गुना हो जाएगा
View Solutionएक 10 m ऊँचाई का टैंक ऊपरी सिरे पर खुला है, इसमें पूर्ण ऊँचाई तक जल भरा है। टैंक में दो छोटे छिद्र बनाये जाते है, एक छिद्र ठीक मध्य में तथा दूसरा तली पर। अतः मध्य तथा तली के क्षेत्र से निर्गत जल के वेगों का अनुपात है
View Solutionसीमान्त वेग v से, नगण्य घनत्व के श्यान माध्यम में एक छोटी गेंद गिरती है। एक अन्य दोगुनी त्रिज्या व समान द्रव्यमान की गेंद का उसी श्यान माध्यम में गिरने पर सीमान्त वेग होगा
View Solution1.25 सेमी व्यास के नल से जल `5xx10^(-5)` मी`"^(3)`/से की दर से प्रवाहित हो रहा है। जल का घनत्व तथा श्यानता गुणांक क्रमशः `10^(3)kgm^(-3)` तथा `10^(-3)` पास्कल-सेकंड है। तब जल का प्रवाह होगा
View Solutionएक असमान अनुप्रस्थ परिच्छेद की क्षैतिज नलिका में द्रव प्रवाह धारा रेखीय है। नलिका में उस बिन्दु पर जहाँ अनुप्रस्थ परिच्छेद 10 `cm^(2)` है, वहाँ पर जल का वेग `1 ms^(-1)` तथा दाब 2000 पास्कल है। उस बिन्दु पर दाब, जहाँ अनुप्रस्थ परिच्छेद 5 `cm^(2)` है, होगा :
View Solutionकिसी बन्द नल से जुड़े हुए मैनोमीटर का पाठ्यांक `4.5xx10^(5)` पास्कल है। जब नल को खोल दिया जाता है, तब मैनोमीटर का पाठ्यांक गिरकर `4xx10^(5)` पास्कल हो जाता है। जल के प्रवाह का वेग है
View Solution1mm त्रिज्या के एक एल्युमीनियम के गोले की 20°C जल में गिरने पर प्राप्त सीमांत गति होगी
(माना प्रवाह पटलित है, Al का विशिष्ट गुरुत्व = 2.7 और `eta=8xx10^(-4)`)
View Solutionदो धातु के गोले, घनत्व `2xx10^(3) kg//m^(3)` के द्रव में एक समान चाल से गिर रहे है। गोले 1 व गोले 2 के पदार्थों का घनत्व क्रमशः `8xx10^(3) kg//m^(3)` तथा `11xx10^(3)kg//m^(3)` है। इनकी त्रिज्याओं का अनुपात है
View Solutionवेन्चुरीमीटर की क्रियाविधि आधारित है
View Solutionतरल प्रवाह के लिये बरनौली प्रमेय का एक अनुप्रयोग है
View Solutionकणित्र का सिद्धान्त आधारित है
View Solution1.5mm त्रिज्या की वर्षा की बूंद 1200 m की ऊँचाई से पृथ्वी सतह पर गिरती है। जल का घनत्व 1000 `kg//m^(3)` तथा वायु का घनत्व 1.2kgm है। यदि बूंद का आकार गोलीय तथा वायु के घर्षण को नगण्य माना जाए तो पृथ्वी सतह पर टकराते क्षण इसका वेग होगा
View Solutionबरनौली समीकरण के अनुसार, `P/(pg)+h+1/2(v^(2))/g=` नियतांक। पद A, B C प्रायः कहलाते हैं
View Solutionकेशनली में (Blood) खून के प्रवाह की दर 200 सेमी.`//`से. है यदि इसका परिच्छेद क्षेत्रफल 0.5 मी`""^2` हो तब प्रवाह का वेग (मि.मी.`//`से.) में होगा :
View Solutionस्प्रे पम्प की बेलनाकार नली का अनुप्रस्थ परिच्छेद `8cm^2` तथा इसके एक सिरे पर `10^-8 m^2` क्षेत्रफल के `40` छिद्र है। यदि इसके अन्दर प्रवाहित द्रव की चाल `0.15 m min^(-1)` हो तब छिद्र से निर्गत द्रव की चाल होगी
View Solutionहीलियम से भरे दो गुब्बारे एक टेबल से बंधी डोरियों के सिरों पर परस्पर अलग तैर रहे है। गुब्बारों की सम्मुख सतह 1 से 2cm दूर है। यदि आप गुब्बारों के मध्य रिक्त स्थान में फूंकते है, तब
View Solutionसमान धातु के दो ठोस गोलों का द्रव्यमान M तथा 8M है। ये एक साथ श्यान द्रव में गिरते है। गोलों के सीमान्त वेग v तथा nv है तब, n का मान है
View Solutionद्रव के धारा रेखीय प्रवाह में कुल उर्जा नियत रहती है
View Solutionसोने (gold) के गोले का किसी श्यान द्रव में सीमान्त वेग 0.2मी/से. है, तब इस द्रव में समान आकार के चाँदी (silver) के गोले का सीमान्त वेग होगा।
सोने का घनत्व = 19.5 kg.`m^(3)`
चाँदी का घनत्व = 10.5 kg.`m^(3)`
श्यानद्रव का घनत्व = 1.5 kg.`m^(3)`
View Solutionएक टैंक में H ऊँचाई तक पानी भरा है इसके ऊपरी सतह से कुछ नीचे एक छेद कर देते है यदि इससे निकलने वाला पानी अधिकतम क्षेतिज परास पर गिरे तो ऊपरी सतह से छिद्र की गहराई होगी।
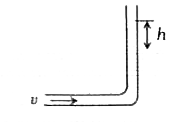
View SolutionL-आकार की काँच की नली बहते जल में चित्रानुसार डूबी है। नीचे का निचला खुला सिरा जल धारा के विपरीत ओर है। यदि जल धारा का वेग v हो तो
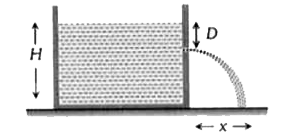
View Solutionकिसी पात्र में H ऊँचाई तक जल भरा है। जल की मुक्त सतह से D गहराई पर छिद्र P से जल बह रहा है। क्षैतिज परास `x` को H व D के पदों में किस सम्बन्ध द्वारा व्यक्त किया जायेगा
View Solutionनिम्न में से कौन बर्नोली सिद्धांत से संबंधित नहीं है
View Solutionजल से पूरा भरा आयताकार पात्र तली में उपस्थित छिद्र से जल बहने के कारण 10 मिनट में खाली हो जाता है। यदि पात्र आधा भरा हो तो इसे खाली होने में कितना समय लगेगा
View Solutionधारारेखीय आकार का एक पिण्ड वायु में h ऊँचाई से गिरकर द्रव सतह पर आता है। द्रव व पिण्ड के घनत्व क्रमश D व `d(Dgtd)` हैं। वह समय जिसके पश्चात् पिण्ड क्षणिक विराम में आएगा, होगा
View Solutionकिसी बड़े पात्र में H ऊँचाई तक जल भरा है। पात्र के तले में एक छोटा छिद्र है। जल स्तर `H/(eta)(etagt1)` तक होने में लगा समय `T_(1)` है। तथा शेष जल बहने में लगा समय `T_(2)`, है यदि `T_(1) = T_(2)` हो, तो `eta` एक मान होगा
View Solutionएक तरल. असगान अनुप्रस्थ परिच्छेद क्षेत्रफल की क्षैतिज नलिका में धारा रेखीय प्रवाह में है। इसके लिए निम्न में से कौन सा कथन सही है
View Solutionबारिश की दो बूदें नीचे की ओर गिरती है। जिनकी समान त्रिज्याएँ r एवं सीमान्त वेग v है, ये मिलकर एक R त्रिज्या की बड़ी बूंद बनाती है। तब इसका सीमान्त वेग होगा।
View Solutionबरनोली प्रमेय निम्न में किस भोतिक संरक्षण नियम पर आधारित है।
View Solutionजब किसी नल से जल धारारेखीय प्रवाह से नीचे गिरता है, तब
View Solutionअसमान परिच्छेद के पाईप में जल स्थिर गति से प्रवाहित है। यदि जिस बिन्दु पर प्रवाह की गति v है वहाँ दाब P तथा जिस बिन्दु पर गति 2v है, वहाँ दाब होगा (जल का घनत्व =`rho`)
View Solutionताप बढाने पर श्यानता का मान
View Solutionबरनौली व्रमेय के अनुसार `P+1/2pV^(2)+pgh=K` (नियतांक) K/P की विमाएं निम्न में से किसके समान होगी
View Solutionश्यानता ज्ञात करने की पॉइजुली की विधि में किस भौतिक राशि का मापन अधिक यथार्थतापूर्वक करना होता है
View Solutionवायुयान को इस प्रकार तैयार किया जाता है कि वायु का वेग
View Solutionदो केशनलियों की लम्बाईयाँ समान हैं, परन्तु त्रिज्याओं का अनुपात 1 : 2 है। नलियों श्रेणी क्रम में संलग्न हैं। उनसे धरारेखीय स्थिति में द्रव प्रवाहित किया जाता है। यदि संयुक्त नली के सिरों पर दबांतर जल स्तम्भ के 1 m दाब के तुल्य हो, तो प्रथम नली सिरों पर दाबांतर होगा
View Solutionकिसी केशनली (त्रिज्या a) से जल धारारेखीय स्थिति में प्रवाहित हो रहा है। दाबांतर P व प्रवाह दर Q है। यदि त्रिज्या a/2 व दाब 2P कर दें, तो प्रवाह दर होगी
View Solutionकिसी बेलनाकार नलिका से एक श्यान द्रव बह रहा है। द्रव के वेग वितरण को उचित रूप से निम्न चित्र द्वारा दर्शाया जा सकता है
View Solution4 सेमी व्यास के एक पाइप से प्रवाहित हो रहे जल का वेग 3 मी/से तत्पश्चात जल 2 सेमी व्यास की नलिका में करता है। नलिका में प्रवाहित जल का वेग है
View Solutionकिसी टैंक में भरे हुए द्रव में गिरती हुई `r` त्रिज्या की एक धात्विक गेंद का उस क्षण वेग क्या होगा, जब इसका त्वरण मुक्त रूप से गिरती हुई वस्तु के त्वरण का आधा है (धातु तथा द्रव के घनत्व क्रमशः p तथा `sigma` हैं तथा द्रव की श्यानता `eta` है)
View Solutionजब कोई वस्तु वायु में गिरती है, तब वस्तु पर लगने वाला वायु प्रतिरोध मुख्यतः वस्तु की आकृति पर निर्भर करता है। तीन विभिन्न आकृतियाँ चित्र में प्रदर्शित हैं। वायु-प्रतिरोधों का कौन सा संयोग भौतिक स्थिति को वास्तविक रूप से दर्शाता है। (वस्तुओं का अनुप्रस्थ परिच्छेद का क्षेत्रफल समान है।
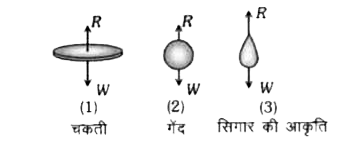
View Solutionत्रिज्या `r` का कोई लघु गोला विरामावस्था से किसी श्यान द्रव में गिरता है। श्यान बल के कारण इसमें ऊष्मा उत्पन्न होती है। गोले के अंतिम (टर्मिनल) वेग पर उत्पन्न ऊष्मा की दर निम्नलिखित में से किसके अनुक्रमानुपाती होती है
View Solution
Ordinary Thinking(तरल प्रवाह ) questions and complete solutions for chapter तरल यांत्रिकि of ERRORLESS PHYSICS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 PHYSICS तरल यांत्रिकि
- Assertion & Reason
- Critical Thinking Objective Questions
- Graphical Questions Objective Questions
- JEE Section (Comprehension type questions)
- JEE Section (Integer type questions)
- JEE Section (JEE(Advanced)2018)
- JEE Section (Matrix Match type questions)
- JEE Section (More than one correct answers)
- Ordinary Thinking(तरल प्रवाह )
- Ordinary Thinking(दाब तथा घनत्व)
- Ordinary Thinking(पास्कल का नियम तथा आर्किमिडीज़ का नियम )
- तरल यांत्रिकि (Self Evaluation Test)