Complete Solutions to Critical Thinking Ojective Questions of chapter किरण प्रकाशिकी of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | किरण प्रकाशिकी |
| ERRORLESS HINDI | Critical Thinking Ojective Questions |
| Number Of Questions | 71 |
| Academic Year | 2023-24 |
एक दीवार पर ऊर्ध्वाधर टंगे d चौड़ाई के एक दर्पण के केंद्र के सामने L दूरी पर एक बिंदु प्रकाश स्रोत B स्थित है | चित्रानुसार एक मनुष्य, दर्पण के समानात्तर 2L दूरी पर स्थित रेखा के अनुदिश गति करता है | वह अधिकतम दूरी जिस पर मनुष्य, प्रकाश स्रोत का प्रतिबिम्ब दर्पण में देख सकता है, होगी
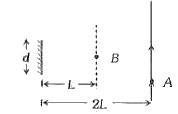
View Solutionदो समतल दर्पणों A और B को चित्रानुसार परस्पर समान्तर रखा गया है | एक प्रकाश किरण A दर्पण के एक सिरे पर ठीक अंदर की ओर स्थित बिंदु पर `30^(@)` के कोण पर आपतित हो रही है | आपतन-तल चित्र तल के सम्पाती है | बाहर निकलने से पहले यह किरण अधिकतम कितनी बार परावर्तित होती है (प्रथम परावर्तन को सम्मिलित करते हुए)

View Solutionदो काँच (अपवर्तनांक = 1.5) की एकरूप छड़ो `S_(1)` तथा `S_(2)` का एक चोर 10 से.मी. वक्रता त्रिज्या की उत्तल सतह है | उनके वक्रसतह एक दूसरे से d दूरी पर दर्शाये चित्रानुसार रखी है | तथा उनके अक्ष एक रेखा (चित्र में असतत रेखा) पर है | यदि प्रकाश के एक बिंदु स्रोत P को चढ़ `S_(1)` के अंदर वक्र सतह se 50 cm की दूरी पर रखने पर इससे निकलने वाली प्रकाश की किरणे छड़ `S_(2)` के अंदर अक्ष के समान्तर हो, तब दूरी d होगी

View Solutionतीन विभिन्न तारो P Q तथा R के प्रकाश के अध्ययन से ज्ञात हुआ कि इनके प्रकाश के स्पेक्ट्रम में अधिकतम तीव्रता क्रमशः P, में बैंगनी, R में हरे तथा Q में लाल रंग के प्रकाश की है | यदि P, Q तथा R के परम् ताप क्रमशः `T_(P), T_(Q)` तथा `T_(R)` है तो, उपरोक्त प्रेक्षणों से यह परिणाम निकाला जा सकता है कि
View Solutionएक छोटी रेखीय वस्तु, जिसकी लम्बाई l है, f फोकस दूरी वाले अवतल दर्पण के सामने उसके ध्रुव से u दूरी पर रखी है | प्रतिबिम्ब का आकार लगभग होगा
View Solutionजब 2R सेंटीमीटर व्यास के बेलनाकार पानी के टेंक से जल निकास समान दर से हो रहा है तब पानी की आभासी गहराई x सेंटीमीटर मिनट की दर से कम हो रही है | एक मिनट में निकले पानी की मात्रा क्यूबिक सेंटीमीटर (c.c.) में है (`n_(1)` = वायु का अपवर्तनांक, `n_(2)` = पानी का अपवर्तनांक)
View Solutionएक ध्रुव से x cm की दूरी पर स्थित एक अवतल दर्पण के सामने रखी वस्तु का वास्तविक प्रतिबिम्ब 3 गुना आवर्धित होता है | यदि उसे (x + 5) cm की दूरी पर रखा जाए तो प्रतिबिम्ब का आवर्धन 2 गुना रह जायेगा | तब दर्पण की फोकस दूरी होगी
View Solutionएक पारदर्शी छड़ पर प्रकाश, छड़ से कुछ कोण बनाते हुए प्रवेश करता है | छड़ का अपवर्तनांक n है | छड़ के पदार्थ के अपवर्तनांक के किस मान के लिए प्रकाश छड़ में प्रवेश करने के पश्चात उसकी पार्श्विक सतहों से बाहर नहीं निकलेगा जबकि आपतन कोण का मान कुछ भी हो
View Solution`'f_(1)'` फोकस दूरी का एक अवतल दर्पण, `'f_(2)'` फोकस दूरी के एक उत्तल लेन्स से 'd' दूरी पर रखा गया है | अनंत से आता हुआ एक किरण पुंज, उत्तल लेन्स तथा अवतल दर्पण के इस संयोजन पर टकराता है ओर अपने मार्ग पर अनंत को वापस हो जाता है | तो दूरी d का मान होगा
View Solution15 cm फोकस दूरी के पतले समतलोतल लेन्स से 20 cm दूर एक बिंदु वस्तु स्थित है | यदि समतल-सतह पर पॉलिश की जाए, तब प्रतिबिम्ब निर्मित होगा
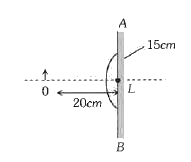
View Solution`n_(1)` अपवर्तनांक वाली एक आयताकार काँच की पट्टी ABCD को `n_(2)(n_(1) lt n_(2))` अपवर्तनांक वाले जल में डुबोया गया है | एक किरण पट्टी के पृष्ठ AB पर चित्रानुसार आपतित होती है | आपतन कोण का अधिकतम मान `alpha_(max)` क्या होगा ताकि किरण केवल CD पृष्ठ से बाहर निकले

View Solutionएक अपसारी प्रकाश किरण पुंज एक बिंदु स्रोत स से `alpha` अपसरण कोण से, एक काँच की पट्टी पर चित्रानुसार सममिति रूप से आपतित हो रही है | दो बहरी किरणों के आपतन कोण समान है | यदि काँच की पट्टी की मोटाई t तथा अपवर्तनांक n है तो निर्गत पुंज का अपसरण कोण है
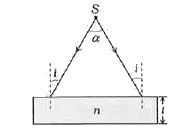
View Solutionएक अवतल दर्पण को खाली टंकी की तली में इस प्रकार रखा है कि इसका पृष्ठ ऊपर की ओर तथा अक्ष ऊर्ध्वाधर हो, तब सूर्य प्रकाश दर्पण पर अभिलंबवत आपतित होता है तो यह दर्पण से 32 सेमी. दूरी पर फोकस होता है, यदि टंकी की पानी `(mu = (4)/(3))` से 20 सेमी. ऊँचाई तक भर दिया जाये तो प्रकाश किरणे अब फोकस होंगी
View Solution4 सेमी. व्यास वाले गोले के अंदर वायु का बुलबुला व्यास के अनुदिश देखने पर आँख के निकट वाले पृष्ठ से 1 सेमी. पर दिखाई देता है | यदि `""_(a)mu_(g) = 1.5` तो बुलबुले की अपवर्तनांक सतह से दूरी होगी
View Solutionबीकर के अंदर चित्रानुसार रखी h ऊँचाई की एक पतली छड़ का ऊपरी सिरा प्रेक्षक को एक छिद्र से दिखाई देता है | बीकर की ऊँचाई 3 h तथा त्रिज्या h है| तब बीकर को 2 h ऊँचाई तक किसी द्रव से भर देते है तो प्रेक्षक क छड़ का निचला सिरा दिखाई देने लगता है द्रव का अपवर्तनांक होगा
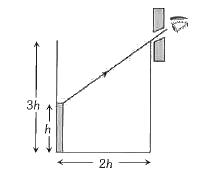
View Solutionएक प्रकाश किरण काँच-पानी सम्पर्क पृष्ठ पर i कोण से आपतित होती है " अन्त में यह पानी के पृष्ठ के समान्तर निर्गत होती है | `mu_(g)` का मान होगा

View Solutionएक द्वि-उत्तल लेन्स की फोकस दूरी f है | यह फोकस तल में सूर्य का r त्रिज्या का व्रतीय प्रतिबिम्ब निर्मित करता है तब
View Solutionअवतल दर्पण की फोकस दूरी ज्ञात करने के u-v विधि प्रयोग में एक छात्र ध्रुव P से x दूरी पर मुख्य अक्ष पर वस्तु पिन A रखता है | छात्र पिन तथा इसका उल्टा प्रतिबिम्ब PA रेखा में नेत्र द्वारा कुछ दूरी से देखता है | तब छात्र अपनी आँख बाई ओर खिसकाता है तब प्रतिबिम्ब वस्तु के दायी ओर खिसकता प्रतीत होता है, तब
View Solutionएक समतल-उत्तल लेन्स का व्यास 6 सेमी है तथा केंद्र पर मोटाई 3 सेमी है यदि लेन्स के पदार्थ में प्रकाश की चल `2xx10^(8)` मी/से हो तो लेन्स की फोकश-दूरी है :
View Solutionकमरे की एक दीवार पर छोटा विघुत बल्ब लगा है इसका 4 m दूर सम्मुख दीवार पर बड़े उत्तल लेन्स से प्रतिबिम्ब प्राप्त किया जाता है | इस कार्य हेतु लेन्स की अधिकतम सम्भव फोकस दूरी होगी
View Solution20 cm फोकस दूरी वाले उत्तल लेन्स से 30 cm की दूरी पर एक प्रकाशिक वस्तु रखी है | लेन्स के दूसरे ओर लेन्स से कितनी दूरी पर एक 10 cm वक्रता त्रिज्या वाला उत्तल दर्पण रखा जाये जिससे वस्तु का सीधा प्रतिबिम्ब वस्तु के ऊपर ही प्राप्त हो
View Solutionचित्र में दिखाये अनुसार एक अभिसारी लेन्स को द्रव से भरे हुए एक वायु प्रकोष्ठ में रखा जाता है | लेन्स की फोकस दूरी + 20 cm है एवं इसका अपवर्तनांक 1.50 है | यदि द्रव का अपवर्तनांक 1.60 है तो इस संयोजन की फोकस दूरी होगी
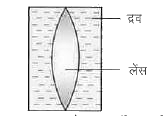
View Solutionएक खोखला उभ्योवतल लेन्स बहुत पतले पारदर्शी पदार्थ का बना है | इस वायु अथवा दो द्रव `L_(1)` एवं `L_(2)` जिनके अपवर्तनांक क्रमशः `n_(1)` एवं `n_(2)` है `(n_(2) gt n_(2) gt 1)` से भरा जा सकता है | लेन्स, समान्तर प्रकाश पुंज को अपसरित करेगा यदि इसे भरा जाये
View Solution15 cm फोकस दूरी वाला एक उभयोत्तल लेन्स के समतल दर्पण के सामने रखा है | लेन्स तथा दर्पण के बीच की दूरी 10 cm है | एक छोटा बिम्ब लेन्स से 30 cm की दूरी पर रखा गया है | इसका अंतिम प्रतिबिम्ब
View Solutionनिम्न में से कौनसा गोलीय लेन्स विक्षेपण नहीं दर्शाता | लेंसों के पृष्ठो की वक्रता त्रिजाये चित्रों से प्रदर्शित है
View Solution30 सेमी. फोकस दूरी वाले उत्तल लेन्स द्वारा अनंत पर स्थित वस्तु के बने प्रतिबिम्ब का आकार 2 सेमी. है | यदि उत्तल लेन्स से 26 सेमी, दूरी पर उत्तल लेन्स व प्रतिबिम्ब के बीच एक 20 सेमी, फोकस दूरी वाला अवतल लेन्स रखा दिया जाये तो प्रतिबिम्ब का नया आकार होगा
View Solution30 सेमी फोकस दूरी का एक उत्तल लेन्स एक 10 सेमी फोकस दूरी वाले अवतल लेन्स के सामने इस प्रकार रखा जाता है कि दोनों की अक्ष एक ही रहे है | एक समानांतर किरण पुंज उत्तल लेन्स पर पड़ने के बाद यदि अवतल लेन्स से भी समानांतर निकले तो दोनों लेंसों के बीच दूरी होगी
View Solutionप्रिज्म का अपवर्तनांक कोण A तथा उसके पदार्थ का अपवर्तनांक `cot ""(A)/(2)` है | न्यूनतम विचलन कोण है
View Solutionकिसी काले कागज पर दो श्वेत बिंदु एक दूसरे से 1 mm दूरी पर अंकित है | इन बिंदुओं को नेत्र, जिसकी पुतली का व्यास 3mm है, द्वारा देखा जाता है | वह अधिकतम दूरी (लगभग) क्या है, जिस पर नेत्र द्वारा इन बिंदुओं को विभेदित किया जा सके [प्रकाश की तरंगदैर्घ्य = 500 nm लीजिए]
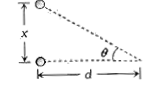
View Solutionएक समकोण प्रिज्म के अंदर आधार के समान्तर गमन करती हुई प्रकाश की किरण उसके विकर्ण पर आपतित होती है | यदि प्रिज्म के पदार्थ का अपवर्तनांक `mu` है तो प्रिज्म के आधार कोण का अधिकतम मान क्या होगा कि विकर्ण से पूर्ण आंतरिक परावर्तन हो सके
View Solutionप्रिज्म के पदार्थ तथा द्रव के अपवर्तनांक क्रमशः 1.56 तथा 1.32 है चित्रानुसार अपवर्तन के लिए `theta` का मान है
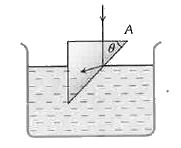
View Solutionएक गोलीय सतह जिसकी त्रिज्या R है वायु एवं काँच को विभेदित कर रही है | इस प्रकार कि वक्रता केंद काँच में है | यदि एक बिंदु आकार की वस्तु P वायु में रखी जाये तो इसका वास्तविक प्रतिबिम्ब Q काँच के अंदर बनता है, रेखा PQ सतह को O पर काटती है | यदि PQ = OQ तो दूरी PO होगी
View Solutionएक दुरदर्शी के अभिदृश्यक के लेन्स का व्यास 10 cm है | तथा वह दो वस्तुओं से 1 Km की दूरी पर स्थित है | यदि प्रकाश की औसत तरंगदैर्घ्य 5000 Å हो तब इन वस्तुओं के बीच की कम से कम वह दूरी जिसे दुरदर्शी विभेदित कर सके, होगी
View Solutionएक प्रकाश किरण, प्रकाशीय सघन माध्यम से विरल माध्यम में प्रवेश करती है | दोनों माध्यमों के लिए क्रांतिक कोण C है, किरण के लिए अधिकतम सम्भव विचलन होगा
View Solutionएक अंतरिक्ष यात्री 400 km ऊँचाई पर किसी अंतरिक्ष यान से पृथ्वी की सतह को देख रहा है यदि अंतरिक्ष यात्री के नेत्र की पुतली का व्यास 5 mm तथा दृश्य प्रकाश की तरंगदैर्घ्य 500 nm है तो यात्री लगभग किस आकार की रेखीय वस्तुओं को विभेदित देख सकता है
View Solutionएक कार में 20 cm फोकस दूरी का पार्श्व-दर्शन उत्तल दर्पण लगा हुआ है | 2.8 m पीछे एक दूसरी कार, पहली कार को 15 m/s की आपेक्षिक चाल से गति कर पकड़ती है | पहली कार के दर्पण में देखी गई दूसरी कार के प्रतिबिम्ब की चाल है
View Solutionएक झील के पानी की सतह से 20 m की ऊँचाई पर एक गेंद छोड़ी जाती है | पानी का अपवर्तनांक 4/3 है | झील में स्थित एक मछली, जो गेंद के गिरने की रेखा में है, गिरती हुई गेंद को देख रही है | जब गेंद पानी की सतह से 12.8 m ऊपर है उस समय मछली गेंद की गति को देखेगी
View Solutionहम एक परमाणु के भीतर देखना चाहते है | यह मानते हुए कि परमाणु का व्यास 100 pm है इसका अर्थ है कि मानिए किसी उपकरण को 10 pm चौड़ाई विभेदित करती है | यदि एक इलेक्ट्रॉन माइक्रोस्कोप को प्रयुक्त किया जाये तब आवश्यक न्यूनतम इलेक्ट्रॉन ऊर्जा है (लगभग)
View Solutionजल-सतह से D गहराई पर एक प्रकाश बल्ब स्थित है | त्रिज्या R की अपारदर्शी चकती जल की सतह पर बल्ब के ठीक ऊपर स्थित है | जल सतह द्वारा बल्ब दिखाई नहीं देता तब (n = जल का अपवर्तनांक)
View Solutionएक अवतल दर्पण जल (अपवर्तनांक = 1.33) से भरे हुए बीकर के ऊपर चित्रानुसार रखा हुआ है | बीकर की तली में स्थित वस्तु का प्रतिबिम्ब जल सतह से 25 cm नीचे बनता है | दर्पण की फोकस दूरी है
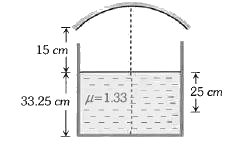
View Solutionएक छोटी वस्तु की 30 cm फोकस दूरी वाले एक पतले उत्तल लेन्स की बाई ओर 50 cm की दूरी पर रखा गया है | 100 cm की वक्रता त्रिज्या वाले एक उत्तल गोलाकार दर्पण को लेन्स की दाई ओर 50 cm की दूरी पर रखा गया है | दर्पण को इस तरह से झुकाया गया है कि दर्पण का अक्ष लेन्स के अक्ष से `theta = 30^(@)` का कोण बनाता है, जैसा चित्र में दर्शाया गया है
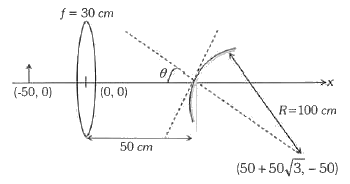
यदि निर्देशांक पद्धति का मूल बिंदु लेन्स के मध्य में हो तो जहाँ प्रतिबिम्ब बना है उस बिंदु का निर्देशांक (x, y), सेंटीमीटर में, क्या होंगे
View Solutionयदि `epsi_(0)` व `mu_(0)` किसी स्थान की विघुतशीलता एवं पारगम्यता हो तथा `epsi` व `mu` माध्यम का सापेक्ष मात्राएँ हो तब माध्यम का अपवर्तनांक क्या होगा
View Solutionकाँच (अपवर्तनांक =1.5) से बने एक टैंक की तली मोटी है | इसमें अपवर्तनांक `mu` का एक द्रव भरा है | एक छात्र पाता है कि किसी भी आपतन कोण i (चित्र देखिये) पर द्रव में आपतित प्रकाश की किरण के लिए द्रव-काँच अंतरपरष्ठ से परावर्तित किरण, कभी भी पूर्णतया ध्रुवित नहीं होती है | ऐसा होने के लिए, `mu` का न्यूनतम मान होगा
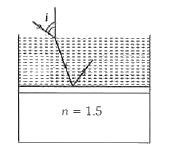
View Solutionकाँच (अपवर्तनांक =1.5) से बने एक टैंक की तली मोटी है | इसमें अपवर्तनांक `mu` का एक द्रव भरा है | एक छात्र पाता है कि किसी भी आपतन कोण i (चित्र देखिये) पर द्रव में आपतित प्रकाश की किरण के लिए द्रव-काँच अंतरपरष्ठ से परावर्तित किरण, कभी भी पूर्णतया ध्रुवित नहीं होती है | ऐसा होने के लिए, `mu` का न्यूनतम मान होगा
View Solutionदो समतल दर्पणों (`M_(1)` तथा `M_(2)`) को परस्पर ऐसे कोण पर रखा गया है जिससे प्रकाश की एक किरण जब `M_(2)` के समान्तर जाती हुयी `M_(1)` पर आपतित होती है तो अन्तः वह `M_(2)` से `M_(1)` के समान्तर परावर्तित होती है | दर्पणों के बीच कोण का मान होगा
View Solutionअपवर्तनांक `mu_(1)` तथा फोकस दूरी `f_(1)` दूरी के एक समतलोत्तल लेन्स को अपवर्तनांक `mu_(2)` तथा फोकस दूरी `f_(2)` के दूसरे समतल-अवतल लेन्स के सम्पर्क में रखा गया है | यदि प्रत्येक गोलीय फलक की वक्रता त्रिज्या R है तथा `f_(1) = 2f_(2)` है तो `mu_(1)` तथा `mu_(2)` में सम्बन्ध होगा
View Solutionमाना कि आँख एक एकल अपवर्तक पृष्ठ है इस पृष्ठ की वक्रता त्रिज्या कोर्निया की वक्रता त्रिज्या (7.8 mm) के बराबर है | यह पृष्ठ अपवर्तनांक 1 तथा 1.34 के माध्यमों को पृथक करता है | इस अपवर्तक पृष्ठ से वह दूरी जिस पर प्रकाश की समान्तर किरणे फोकस में आयेगी, होगी
View Solutionक्राउन काँच के प्रिज्म के अपवर्तनांक परिवर्तन को आपतित प्रकाश की तरंगदैर्घ्य के साथ दिखाया गया है | यदि `D_(m)` न्यूनतम विचलन कोण है तो निम्न में से कौनसा ग्राफ सही है
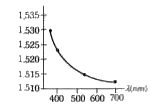
View Solution0.3 फोकस दूरी के एक उत्तल लेन्स से कोई वस्तु 20 m की दूरी पर है | लेन्स द्वारा वस्तु का प्रतिबिम्ब बनता है | यदि यह वस्तु लेन्स से दूर 5 m/s की चाल से जाती है तो प्रतिबिम्ब की चाल ओर दिशा होगी
View Solutionएक द्वि-झिरी प्रयोग में, हरा प्रकाश (5303 Å) द्वि-झिरी पर पड़ता है | झिरियों के बीच की दूरी 19.44 `mum` तथा इनकी चौड़ाई 4.05 `mum`. है | प्रथम तथा द्वितीय विवर्तन निमनिष्ठ के बीच में कितनी दीप्त फ़्रिजे है
View Solutionएक एकवर्णीय प्रकाश किसी समबाहु त्रिभुजीय प्रिज्म पर एक निश्चित कोण पर आपतित होता है ओर उसका न्यूनतम विचलन होता है | यदि प्रिज्म के पदार्थ का अपवर्तनांक `sqrt(3)`हो , तो आपतन कोण है
View Solutionदिये गये चित्र में लेन्स संयोजन से बने प्रतिबिम्ब की स्थिति व प्रकृति होगी (`f_(1),f_(2)` फोकस दूरियाँ है)
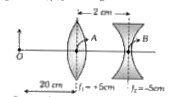
View Solutionएक उभयोत्तल लेन्स से एक वास्तविक प्रतिबिम्ब के बनने का चित्र में दर्शाया गया है
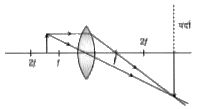
वस्तु तथा पर्दे की स्थिति को बिना विचलित किए इस सम्पूर्ण संयोजन को यदि पानी में डुबो जाये तो पर्दे पर क्या दिखेगा
View Solutionएक समतल-उत्तल लेन्स (फोकस दूरी `f_(2)`, अपवर्तनांक `mu_(2)`, वक्रता त्रिज्या R) एक समतल-अवतल लेन्स (फोकस दूरी `f_(1)`, अपवर्तनांक `mu_(1)`, वक्रता त्रिज्या R) में ठीक बैठ जाता है | उनके समतल पृष्ठ एक दूसरे के समान्तर है | इस संयोजन की फोकस दूरी होगी
View Solution20 cm फोकस लम्बाई वाले एक अभिसारी लेन्स के सामने 40 cm की दूरी पर एक सीधी वस्तु को रखा गया है | लेन्स के दूसरे ओर 60 cm की दूरी पर 10 cm फोकस लम्बाई वाले एक अभिसारी दर्पण को रखा गया है | अंतिम प्रतिबिम्ब की स्थित ओर आकार होगा
View Solutionचित्र में l = 2 मीटर लम्बे तथा `d = 20 mum` व्यास के एक प्रकाश तंतु को दिखाया है | यदि प्रकाश की किरण इस तंतु के एक सिरे पर `theta_(1) = 40^(@)` कोण पर आपतित होती है तो दूसरे सिरे से निकलने से पूर्व इसके परावर्तनो की लगभग संख्या होगी (फाइबर का अपवर्तनांक 1.31 है ओर `sin 40^(@) = 0.64` )
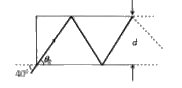
View Solutionएक तारे से आ रहे 500 nm तरंगदैर्घ्य के प्रकाश को संसूचित करने के लिए 200 cm व्यास के अभिदृश्यक लेन्स वाले दुरदर्शी की विभेदन सीमा ज्ञात कीजिये
View Solutionएक उत्तल लेन्स (फोकस दूरी 20 cm) तथा एक अवतल दर्पण, जिनके मुख्य अक्ष एक ही रेखा में है, को एक दूसरे से 80 cm की दूरी पर रखा गया है, अवतल दर्पण उत्तल लेन्स के दाहिनी तरफ रखा है | जब एक वस्तु उत्तल लेन्स के बायीं तरफ 30 cm की दूरी पर रखी जाती है, तो उसका प्रतिबिम्ब उसी स्थान पर ही रहता ह, भले ही अवतल दर्पण को उसकी स्थिति से हटा दिया जाये | वस्तु की अधिकतम दूरी, जिसके लिए वह अवतल दर्पण खुद से ही आभासी प्रतिबिम्ब बनाये, होगी
View Solutionअपने चेहरे को देखने के लिए एक 0.4 m फोकस दूरी का अवतल दर्पण उपयोग करते है | यदि अपने प्रतिबिम्ब को सीधा ओर 5 गुना बडा देखना हो तो दर्पण की चेहरे से दूरी का मान होगा
View Solutionएक समतल-उत्तल ओर एक समतल-अवतल लेन्स, जिसकी वक्रता त्रिज्या R है वो अलग पदार्थो के बने है | इन दोनों को चित्रानुसार चिपका दिया जाता है है | यदि लेन्स-१ के पदार्थो का अपवर्तनांक `mu_(1)` तथा लेन्स-2 के पदार्थ का अपवर्तनांक `mu_(2)` है तो इस संयोजन की फोकस दूरी होगी

View Solutionएक प्रकाश की किरण AO निर्वात से काँच से `60^(@)` के कोण पर आपतित है तथा इसका अपवर्तन `30^(@)` के कोण पर जब के समदीश चित्रानुसार होता है | इस किरण की A से B तक प्रकाशित पथ लम्बाई होगी
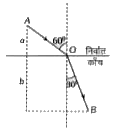
View Solution1.5 अपवर्तनांक के एक पतले उत्तल लेन्स L को, किसी समतल दर्पण M की सतह पर रखते है | जब एक पिन को A पर रखते है, तब इसका वास्तविक किन्तु उल्टा प्रतिबिम्ब, दिखाये चित्रानुसार पर ही बनता है | दिया है OA = 18 cm | अपवर्तनांक `mu_(1)` के एक द्रव को लेन्स तथा दर्पण के बीच डालने पर, पिन के वास्तविक एवं उलटे प्रतिबिम्ब को A पर ही पाने के लिए पिन को A तक इस प्रकार उठाते है कि OA = 27 cm | `mu` का मान होगा
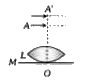
View Solution20 cm फोकस दूरी के एक उत्तल लेन्स से किसी वस्तु के प्रतिबिम्ब का आवर्धन 2 ही होता जब वस्तु का लेन्स से दो दूरियों `x_(1)` तथा `x_(2)(x_(1) gt x_(2))` पर रखते है | `x_(1)` ओर `x_(2)` अनुपात है
View Solutionएक दुरदर्शी के अभिदृश्यक लेन्स का व्यास 250 cm है | एक दूर स्थित वस्तु से आने वाले तरंगदैर्घ्य 600 nm के प्रकाश के लिए दुरदर्शी की विभेदन सीमा होगी, लगभग
View Solutionदिये गए ग्राफ के एक पतले लेन्स के आवर्धन m को प्रतिबिम्ब की दूरी v के साथ दर्शाया गया है | इस लेन्स की फोकस दूरी क्या होगी
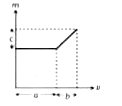
View Solutionअपवर्तनांक `mu_(1)` के एक द्रव में अपवर्तनांक `mu_(2)(mu_(1) lt mu_(2))` के पारदर्शी गुटके को डुबोया जाता है | प्रकाश की एक किरण इस गुटके के पृष्ठ पर द्रव AB पर द्रव से, चित्रानुसार, `theta` कोण पर आपतित होती है | पृष्ठ BC के बिंदु E पर पूर्ण आंतरिक परावर्तन होने के लिए, `theta` का कौनसा सम्बन्ध संतुष्ट करेगा
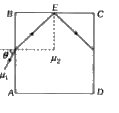
View Solutionएक सूक्ष्मदर्शी के अभिदृश्यक लेन्स की संख्यात्मक द्वारक का मान 1.25 है | यदि 5000 Å तरंगदैर्घ्य का प्रकाश प्रयोग करे तो, दो बिंदुओं को अलग-अलग देखने के लिए उनके बीच की न्यूनतम दूरी होगी
View Solution40 cm यहाँ वक्रता त्रिज्या का एक अवतल दर्पण, आरेख में दर्शाये गए अनुसार, एक गिलास की तली में रखा है | गिलास में 5 cm ऊँचाई तक जल भरा है | एक छोटा सा कण जल की सतह पर तैर रहा है | गिलास के ठीक ऊपर से देखने पर, इस का प्रतिबिम्ब जल की सतह से d दूरी पर है | तो, d का निकट मान होगा (पानी का अपवर्तनांक = 1.33)

View Solutionइंद्रधनुष के संदर्भ में गलत उत्तर चुनिए
View Solutionफोकस दूरी f के दो समान पतले समतलोत्तल लेन्स एक दूसरे के सम्पर्क में सपाक्ष इस प्रकार रखे गए है कि संयोजन की फोकस दूरी `F_(1)` है | जब इन दोनों के बीच के स्थान में ग्लिसरीन (जिसका अपवर्तनांक काँच के अपवर्तनांक `(mu = 1.5)` के बराबर है ) भर दी जाती ह, तो तुल्य फोकस दूरी `F_(2)` है | अनुपात `F_(1) : F_(2)` होगा
View Solutionपूर्ण आंतरिक परावर्तन में जब सम्पर्क के माध्यमों के युगल के लिए आपतन कोण क्रांतिक कोण के बराबर होता है, तो अपवर्तन कोण कितना होगा
View Solution
Critical Thinking Ojective Questions questions and complete solutions for chapter किरण प्रकाशिकी of ERRORLESS PHYSICS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 PHYSICS किरण प्रकाशिकी
- Assertion & Reason
- Critical Thinking Ojective Questions
- Grahical Questions Ojective Questions
- JEE Section
- JEE Section (Comprehension type questions)
- JEE Section (Integer type questions)
- JEE Section (JEE (Advanced) 2018)
- JEE Section (Reasoning type questions)
- Ordinary Thinking Objective Questions ( प्रिज्म एंव प्रकाश का विक्षेपण)
- Ordinary Thinking Objective Questions (गोलीय दर्पण)
- Ordinary Thinking Objective Questions (पूर्ण आन्तरिक परावर्तन )
- Ordinary Thinking Objective Questions (प्रकाशमिति)
- Ordinary Thinking Objective Questions (मानव नेत्र एवं लेन्स कैमरा)
- Ordinary Thinking Objective Questions (वक्रीय सतह पर अपवर्तन)
- Ordinary Thinking Objective Questions (समतल दर्पण)
- Ordinary Thinking Objective Questions (समतल सतह पर प्रकाश का अपवर्तन)
- Ordinary Thinking Objective Questions (सूक्ष्मदर्शी एवं दूरदर्शी)
- Self Evaluation Test (किरण प्रकाशिकी)