Complete Solutions to EXAMPLE of chapter TWO DIMENSIONAL ANALYTICAL GEOMETRY-II of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | TWO DIMENSIONAL ANALYTICAL GEOMETRY-II |
| FULL MARKS | EXAMPLE |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
Find the general equation of a circle with centre (-3,-4) and radius 3 units.
View SolutionFind the equation of the circle described on the chord 3x+y+5=0 of the circle `x^(2)+y^(2)=16` as diameter.
View SolutionDetermine whether x+y-1=0 is the equation of a diameter of the circle `x^(2)+y^(2)-6x+4y+c=0` for all possible values of c.
View SolutionFind the general equation of the circle whose diameter is the line segment joining the points (-4,-2) and (1,1)
View SolutionExamine the position of the point (2,3) with respect to the circle `x^(2)+y^(2)-6x-8y+12=0`.
View SolutionThe line 3x+4y-12=0 meets the coordinate axes at A and B. find the equation of the circle drawn on AB as diameter.
View SolutionA line `3x+4y+10=0` cuts a chord of length 6units on a circle with centre of the circle (2,1). Find the equation of the circle in general form.
View SolutionA circle of radius 3 units touches both the axes. Find the equations of all possible circles formed in the general form.
View SolutionFind the centre and radius of the circle
`3x^(2)+(a+1)y^(2)+6x-9y+a+4=0`.
View SolutionFind the equation of the circle passing through the points (1,1), (2,-1), and (3,2).
View SolutionFind the equation of the tangent and normal to the circle `x^(2)+y^(2)=25` at P(-3,4)
View SolutionIf `y=4x+c` is a tangent to the circle `x^(2)+y^(2)=9`, find c.
View SolutionA road bridge over an irrigation canal have two semi circular vents each with a span of 20 m and the supporting pillars of width 2m. Use figure to write the equations that represent the semi verticular vents.

View SolutionFind the length of the Latus rectum of the parabola `y^(2)=4ax`.
View SolutionFind the length of Latus rectum of the ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`.
View SolutionFind the equation of the parabola with vertex (-1, -2), axis parallel to y-axis and passing through (3, 6).
View SolutionThe equation of the ellipse with foci `(pm2,0)` vertices `(pm3,0)` is:
View SolutionFind the equation of the ellipse whose eccentricity is `1/2`, one of the foci is (2, 3) and a directrix is x = 7. Also find the length of the major and minor axes of the ellipse.
View SolutionFor the ellipse `4x^(2)+y^(2)+24x-2y+21=0`, find the centre, vertices, and the foci. Also prove that the length of latus rectum is 2.
View SolutionFind the equation of the hyperbola with vertices `(0,+-4)` and foci `(0,+-6)`.
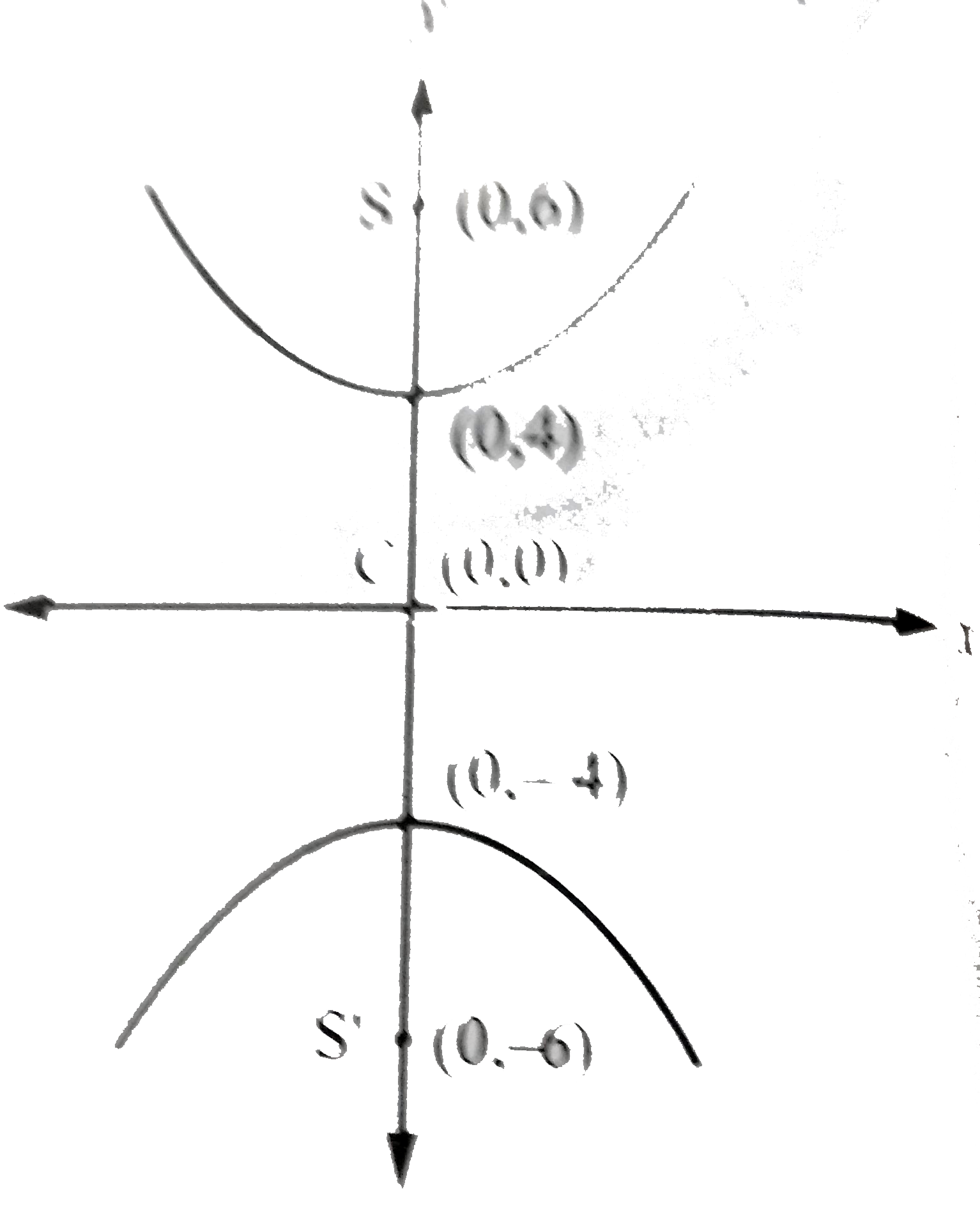
View SolutionFind the vertices, foci for the hyperbola `9x^(2)-16y^(2)=144.`
View SolutionFind the centre, foci, and eccentricity of the hyperbola `11x^(2)-25y^(2)-44x+50y-256=0`
View SolutionThe orbit of Halley's comet is an ellipse 36.18 astronomical units long and 9.12 astronomical units wide. Find its eccentricity.
View SolutionIdentify the type of the conic for the following equations:
1. `16y^(2)=-4x^(2)+64`
2. `x^(2)+y^(2)=-4x-y+4`
3. `x^(2)-2y=x+3`
4. `4x^(2)-9y^(2)-16x+18y-29=0`
View SolutionFind the equations of tangent and normal to the parabola `x^(2)+6x+4y+5=0` at `(1,-3)`.
View SolutionFind the equations of tangent and normal to the ellipse `x^(2)+4y^(2)=32` when `theta=(pi)/(4)`.
View SolutionA semielliptical archway over a one-way road has height of 3m and a width of 12m. The truck has a width of 3m and a height of 2.7m. Will the truck clear the opening of the archway?

View SolutionThe maximum and minimum distances of the Earth from the Sun respectively are `152xx10^(6)` km and `94.5xx10^(6)` km. the Sun is at one focus of the elliptical orbit. Find the distance from the sun to the other focus.
View SolutionA concrete bridge is designed as a parabolic arch. The road over bridge is 60 m long and the maximum height of the arch is 15m. What is the equation of the parabola.
View SolutionThe parabolic communication antenna has a focus at 3m distance from the vertex of the antenna. Find the width of the antenna 8m from the vertex.
View SolutionThe equation `y=(1)/(32)x^(2)` models cross sections of parabolic mirrors that are used for solar energy. There is a heating tube located at the focus of each parabola, how high is this tube located above the vertex of the parabola ?

View SolutionA search light has a parabolic reflector (has a cross section that forms a 'bowl'). The parabolic bowl is 40 cm wide from rim to rim and 30cm deep. The bulb is located at the focus.
(1) what is the equation of the parabola used for reflector?
(2) How far from the vertex is the bulb to be placed so that the maximum distance covered?
View SolutionAn equation of the elliptical part of an optical lens system is `(x^(2))/(16)+(y^(2))/(9)=1`. The parabolic part of the system has a focus in common with the right focus of the ellipse. The vertex of the parabola is at the origin and the parabola opens to the right. determine the equation of the parabola
View SolutionA room 34m long is constructed to a whispering gallery. The room has an elliptical ceiling, as shown in figure. If the maximum height of the ceiling is 8m, determine where the foci are located .
View SolutionIf the equation of the ellipse is `((x-11)^(2))/(484)+(y^(2))/(64)=1` (x and y are measured in centimeters) where to the nearest centimeter, should the patient's kidney stone be placed so that the reflected sound hits the kidney stone?
View SolutionTwo coast guard stations are located 600 km apart at points A(0,0) and B(0,600). A distress signal from a ship at P is received at slightly different times by two stations. It determined that the ship is 200 km farther from station A than it is from station B. Determine the equation of hyperbola that passes through the location of the help.
View SolutionCertain telescopes contain both parabolic mirror and a hyperbolic mirror. In the telescope shown in figure the parabola and hyperbola share focus `F_(1)` which is 14m above the vertex of the parabola. The hyperbola's second focus `F_(2)` is 2m above the parabola's vertex. The vertex of the hyperbolic mirror is 1m below `F_(1)`. Position a coordinate systemm with the origin at the centre of the hyperbola and with the foci on the y-axis. then find the equation of the hyperbola.
View Solution
EXAMPLE questions and complete solutions for chapter TWO DIMENSIONAL ANALYTICAL GEOMETRY-II of FULL MARKS MATHS (TAMIL ENGLISH) of Class 12