Complete Solutions to प्रतियोगिता सामग्री बहुविकल्पीय प्रश्न : एक सही विकल्प of chapter तरंग प्रकाशिकी of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | तरंग प्रकाशिकी |
| GRB PUBLICATION HINDI | प्रतियोगिता सामग्री बहुविकल्पीय प्रश्न : एक सही विकल्प |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
`((1)/(2) (i + sqrt(3j)))` दिशा में चल रही प्रकाश की एक किरण , एक समतल दर्पण पर आपतित होती है। परावर्तन के बाद यह `((1)/(2) (i - sqrt(3j)))` दिशा में जाती है। आपतन कोण है
View Solutionदो समतल दर्पण , एक दूसरे के साथ `60^(@)` के कोण पर आनत हैं। एक बिन्दु वस्तु उनके बीच रखी जाती है। दोनों दर्पणों द्वारा बने प्रतिबिम्बों की कुल संख्या है
View Solutionदो समतल दर्पण A और B एक दूसरे के समान्तर सरेखित हैं जैसा कि चित्र VI.1 मे दिखाया गया है। प्रकाश कि एक किरण , A के एक सिरे के मात्र अन्दर किसी बिन्दु `30^(@)` के कोण पर आपतित है। आपतन तल , चित्र के तल के साथ संपाती है। बाहर निकलने से पहले किरण अधिकतम जितनी बार परावर्तित होती है (पहली बार को मिला कर) , वह है

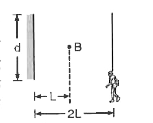
View Solutionप्रकाश का एक बिन्दु स्त्रोत्र B , दीवार पर ऊर्ध्वाधर रूप से टंगे d चौड़ाई के दर्पण के सामने इसके केन्द्र से L दुरी पर रखा जाता है। चित्र VI.2 में दिखाए अनुसार एक व्यक्ति , दर्पण से 2L दुरी पर इसके समान्तर रेखा के अनुदिश इसके सामने चलता है। अधिकतम दुरी , जहाँ तक वह दर्पण में स्त्रोत्र का प्रतिबिम्ब देख सकता है , वह है
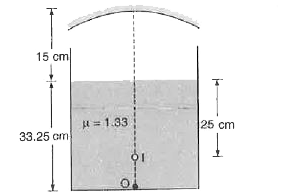
View Solutionएक बर्तन , 33.25 cm की ऊँचाई तक जल `(mu =1.33 )` से भरा जाता है। एक अवतल दर्पण, जल के स्तर से 15 cm ऊपर रखा जाता है [चित्र VI. 3] और पेंदी पर रखी एक वस्तु का प्रतिबिम्ब , जल - स्तर से 25 cm नीचे बनता है। दर्पण की फ़ोकस दुरी है
View Solution`u-v` विधि द्वारा अवतल दर्पण की फोकस दूरी f ज्ञात करने के लिए एक प्रयोग में, एक छात्र/छात्रा ध्रुव P से x दूरी पर बिंब पिन A को मुख्य अक्ष पर रखता/रखती है। छात्र/छात्रा PA के साथ अपनी आंखों को संरेखित करते हुए, दूरी से पिन और उसके उल्टे प्रतिबिंब को देखता/ देखती है। जब छात्र/छात्रा अपने नेत्र को बाईं ओर स्थानांतरित करता/ करती है, तो प्रतिबिंब, बिंब पिन के दाईं ओर दिखाई देता है। तब
View Solutionएक बिन्दु वस्तु , एक समतल दर्पण के सामने रखी जाती है। यदि वस्तु और दर्पण , एक सरल रेखा के अनुदिश एक दूसरे से v चाल से दूर हटना शुरू क्र दें , तो दर्पण के सापेक्ष प्रतिबिम्ब की चाल है
View Solutionएक प्रक्षेक एक स्तर समतल दर्पण की ओर `4 m//s` की चाल से जाता है। उसका प्रतिबिम्ब उसकी ओर किस चाल से चलेगा ?
View SolutionL लम्बाई की एक छोटी वस्तु , f फ़ोकस दुरी वाले अवतल दर्पण से u दुरी पर इसके मुख्य अक्ष पर पड़ी है। इसके प्रतिबिम्ब का आकार होगा
View Solutionजब प्रकाश की किरण माध्यम i से माध्यम j में जाए और यदि `""^(i)u_(j)`, अपवर्तनांक दर्शाए , तो `""^(2)mu_(1) xx ""^(3)mu_(2) xx ""^(4)mu_(3)` का गुणनफल होगा
View Solutionकाँच के सापेक्ष , वायु का अपवर्तनांक `(2//3)` है। वायु के सापेक्ष , हीरे का अपवर्तनांक `(12//5)` है। तब काँच का हीरे के सापेक्ष अपवर्तनांक होगा
View Solutionलम्बवत आपतित किरण के साथ चित्र VI.4 में दर्शाए दो स्लैबों के संयोजन का तुल्य अपवर्तनांक है

View Solutionएक वस्तु किसी द्रव में डुबो दी जाती है ताकि वस्तु अदृश्य हो जाए।
View Solutionजैसा कि चित्र VI.5 में दर्शाया गया है , प्रकाश कि एक किरण , चार पारदर्शक माध्यपों में से गुज़रती है जिनके अपवर्तनांक `mu_(1), mu_(2), mu_(3)` ओर `mu_(4)` हैं। सभी माध्यमों के पृष्ठ समान्तर है। यदि निर्गत किरण , आपतित किरण AB के समान्तर हो , तो अवश्य ही

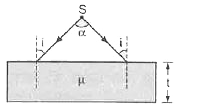
View Solution`alpha` अपसरण कोण वाले बिन्दु स्त्रोत S से अपसरित हो रही प्रकाश कि बीम , चित्र VI.6 में दिखाए अनुसार एक काँच के स्लैब पर सममित रूप में पड़ती है। दो चरम किरणों के आपतन कोण बराबर हैं। यदि काँच के स्लैब कि मोटाई t हो और इसका अपवर्तनांक `mu`, तो निर्गत बीम का अभिसरण कोण है
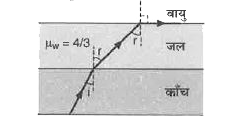
View Solutionप्रकाश कि एक किरण , काँच - जल अन्तरापृष्ठ पर कोण i पर आपतित है। यदि यह अन्त में जल के पृष्ठ के समान्तर बाहर निकले [चित्र VI.7] , तो `mu_(g)` का मान होगा
View Solutionएक बिन्दु वस्तु , 6 cm व्यासार्ध और 1.5 अपवर्तनांक वाले काँच के गोले के केन्द्र पर रखी जाती है। गोले के पृष्ठ से आभासी प्रतिबिम्ब की दुरी है
View Solutionकोई सूक्ष्मदर्शी , कागज़ के एक टुकड़े पर किसी निशान पर फ़ोकसित किया जाता है और तब 3 cm मोटाई और 1.5 अपवर्तनांक वाला काँच का स्लैब , निशान के ऊपर रख दिया जाता है। सूक्ष्दर्शी को कैसे चलाया जाए कि निशान फिर फ़ोकस में आ जाए ?
View Solutionकाँच के स्लैब `(mu = 1.5)` में एक बुलबुला एक ओर से देखे जाने पर 5 cm पर तथा दूसरी ओर से देखे जाने पर 2 cm पर प्रतीत होता है। स्लैब कि मोटाई है
View Solution2R cm व्यास वाले बेलनाकार जल के टैंक में जल कि आभासी गहराई `x cm//min` की दर से घट रही है जब जल किसी स्थिर दर से बाहर निकाला जा रहा है। निकाले गए जल की मात्रा (`cm^(-3)//min` में) है (यहाँ `mu_(1)` = वायु का अपवर्तनांक और `mu_(2)` = जल का अपवर्तनांक )
View Solutionएक गेंद किसी झील में जल के पृष्ठ के ऊपर 20 m की ऊँचाई से गिराई जाती है। जल का अपवर्तनांक `4//3` है। झील में एक मछली , जो गेंद वाली रेखा में है , गेंद की ओर देख रही है। जिस क्षण गेंद जल के पृष्ठ से 12.8 m ऊपर है , मछली को गेंद की चाल दिखती है (g = 10 m//s^(2) लें)
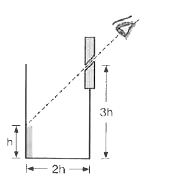
View Solutionएक प्रेक्षक एक सूची - छिंद्र में से h ऊँचाई की पतली छड़ का ऊपर वाला सिरा देख सकता है जो चित्र VI.8 में दिखाए अनुसार रखी गई है। बीकर की ऊँचाई 3h है और इसका व्यासार्ध h है। जब बीकर , 2h ऊँचाई तक किसी द्रव से भर दिया जाता है , तो वः छड़ का nichlaa सिरा देख सकता है। तब द्रव का अपवर्तनांक है
View Solutionएक डिस्क , एक तालाब के पृष्ठ पर रखी जाती है जिसका अपवर्तनांक `(5//3)` है। प्रकाश का एक स्त्रोत , द्रव के पृष्ठ से 4 m नीचे रखा जाता है। डिस्क का जो न्यूनतम व्यासार्ध होना चाहिए , ताकि प्रकाश बाहर न आ सके , वह है
View Solution`mu` अपवर्तनांक वाले पारदर्शक माध्यम में चल रही प्रकाश की एक किरण , माध्यम का वायु से पृथक करने वाले पृष्ठ पर `45^(@)` के आपतन कोण पर है। `mu` के किन मानों के लिए प्रकाश का पूर्ण आन्तरिक परावर्तन हो सकता है ?
View Solutionचित्र VI.9 में दिखाई नई आपतित किरण के लिए पूर्ण आन्तरिक परावर्तन की शर्त पूरी हो जाएगी यदि ब्लॉक का अपवर्तनांक होगा

View Solutionजब एक प्रकाश किरण , एक माध्यम से दूसरे में प्रविष्ट होती है , तो इसका वेग दुगना हो जाता है। पूर्ण आन्तरिक परावर्तन के लिए किरण के लिए क्रांतिक कोण होगा
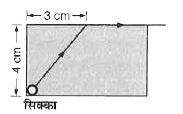
View Solutionएक छोटा सिक्का , किसी द्रव से भरे बीकर की पेंदी पर पड़ा है। सिक्के से एक प्रकाश किरण , द्रव के पृष्ठ तक जाती है और इसके अनुदिशा चलती है [चित्र VI.10]। द्रव में प्रकाश कितनी तेज़ी से चल रहा है ?
View Solutionएक किरण , छोटे कोण A वाले एक प्रिज़्म के एक पृष्ठ पर आपतन कोण i पर आपतित है और सामने वाले पृष्ठ से लम्बवत निर्गत होती है। यदि प्रिज़्म के पदार्थ का अपवर्तनांक `mu` हो , तो आपतन कोण लगभग इनके बराबर है
View Solution`M_(1)` और `M_(2)` माध्यमों में प्रकाश की चालें क्रमशः और हैं। प्रकाश की एक किरण , आपतन कोण i पर माध्यम `M_(1)` से `M_(2)` की ओर प्रविष्ट होती है। यदि किरण का पूर्ण आन्तरिक परावर्तन हो , तो i का मान है
View Solutionयदि प्रकाश , वायु में x दूरी , `t_(1)` सेकण्ड में तय करता है और किसी माध्यम में 10 x दूरी , `t_(2)` सेकण्ड में , तो माध्यम का क्रांतिक कोण होगा
View Solutionजल `(mu = 4//3)` में 12 m की गहराई पर एक गोताखोर आकाश को इस अर्ध - ऊर्ध्वाधर कोण के शंकु में देखता है
View Solutionप्रकाश का एक बिन्दु स्त्रोत , `(5//3)` अपवर्तनांक वाले जल के पृष्ठ से 4 m नीचे रखा जाता है। एक डिस्क का न्यूनतम व्यास , जो जल से आ रहा सारे प्रकाश को रोकने के लिए जल के पृष्ठ पर स्त्रोत के ऊपर रखी जानी चाहिए , है
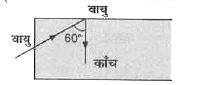
View Solutionवायु से एक प्रकाश किरण , काँच (अपवर्तनांक mu = 1.5) के एक तन्तु के एक सिरे पर आपतित है (जैसे चित्र VI. 11 में दिखाया गया है) और यह पार्श्विक पृष्ट पर `60^(@)` का आपतन कोण बनाती है ताकि इसका पूर्ण आन्तरिक परावर्तन हो। 1 km लम्बे सीधे तन्तु को पार करने में इसे कितना समय लगेगा ?
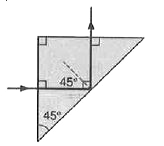
View Solutionएक प्रकाश किरण , `90^(@)` प्रिज़्म के एक फ़लक पर लम्बवत आपतित है और काँच - वायु अन्तरापृष्ठ पर इसका पूर्ण आन्तरिक परावर्तन हो जाता है [चित्र VI.12]। यदि परावर्तन कोण `45^(@)` हो , तो हम यह निष्कर्ष निकालते है कि अपवर्तनांक
View Solutionप्रकाश , किसी प्रिज़्म के एक फ़लक पर `60^(@)` के कोण पर आपतित है जबकि प्रिज़्म के दूसरे फ़लक पर चाँदी चढ़ाई हुई है (प्रिज़्म कोण `30^(@)`। यदि किरण अपने ही पथ से वापस जाए , तो प्रिज़्म के पदार्थ का अपवर्तनांक है
View Solutionजल में से ऊपर की ओर देख रही मछली को बाहर का संसार एक वृत्ताकार क्षितिज में सिमटा नज़र आता है। यदि जल का अपवर्तनांक `4//3` हो ओर मछली जल के पृष्ठ से 12 cm नीचे हो , तो वृत्त का व्यासार्ध (cm में) है
View Solutionजल में चल रही प्रकाश की एक किरण इसके वायु की ओर खुले पृष्ठ पर आपतित है। आपतन कोण `theta` है जो क्रांतिक कोण से कम है। तब
View Solutionश्वेत प्रकाश की एक बीम , एक काँच - वायु अन्तरापृष्ठ पर काँच से वायु की ओर ऐसे आपतित है कि हरे प्रकाश का पूर्ण आन्तरिक परावर्तन मात्र होता है होता है [चित्र VI.13]। वायु में बाहर आने वाले प्रकाश के रंग होंगे

View Solutionप्रकाश की एक बीम , चित्र VI.14 में दिखाए अनुसार क्षेत्र I से क्षेत्र IV की ओर जा रही है। क्षेत्रों I , II , III और IV में अपवर्तनांक क्रमशः और हैं। जिस आपतन कोण `theta` पर बीम, क्षेत्र IV में जाते - जाते रह जाती है , वह है
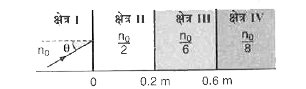
View Solutionप्रकाश कि एक किरण , एक द्रव्यात्मक माध्यम से `60^(@)` के आपतन कोण पर टकराती है। यदि परावर्तित ओर अपवर्तित किरणें एक दूसरे पर लम्बवत हों , तो पदार्थ का अपवर्तनांक है
View Solutionएक पारदर्शी ठोस बेलनाकार छड़ का अपवर्तनांक `2//sqrt(3)` है। इसके सब ओर वायु है। प्रकाश की एक किरण , चित्र VI.15 में दिखाए अनुसार छड़ के एक सिरे के मध्य - बिन्दु पर आपतित है। जिस आपतन को `theta` के लिए प्रकाश किरण , छड़ की दीवार के अनुदिश पृष्ठसर्पी है , वह है

View Solutionएक किरण , प्रिज़्म `ABC (AB = BC)` पर पड़ती है और VI. 16 में दिखाए अनुसार चलती है। प्रिज़्म के पदार्थ के अपवर्तनांक का न्यूनतम मान होना चाहिए

View Solutionप्रकाश की एक किरण , किसी `60^(@)` प्रिज़्म पर न्यूनतम विचलन स्थिति पर आपतित है। प्टिज़्म के पहले फ़लक (अर्थात आपतन फ़लक ) पर अपवर्तन का कोण है
View Solutionएक प्रिज़्म , `sqrt(2)` अपवर्तनांक वाले द्रव से भरी है। यदि प्रिज़्म का कोण `60^(@)` हो , तो न्यूनतम विचलन का कोण है
View Solution`60^(@)` अपवर्तन कोण वाला एक प्रिज़्म , `mu` अपवर्तनांक वाले पदार्थ से बना है। प्रकाश के किसी विशेष तरंगदैर्ध्य के लिए नुय्नतम विचलन का कोण `30^(@)` है। इस तरंगदैर्ध्य के लिए पदार्थ के `mu` का मान है
View Solutionकाँच का अपवर्तनांक , लाल प्रकाश के लिए 1.520 और नीले प्रकाश के लिए 1.525 है। यदि इस काँच के एक प्रिज़्म में लाल और नीले प्रकाश न्यूनतम विचलन के कोण क्रमशः `delta_(1)` और `delta_(2)` हों , तो
View Solutionएक समबाहु प्रिज़्म , एक क्षैतिज पृष्ठ पर रखी जाती है। एक किरण PQ , इस पर आपतित है [चित्र VI. 17]। न्यूनतम विचलन के लिए
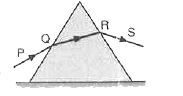
View Solutionलाल और हरी किरणों से बने प्रकाश की बीम , एक आयताकार काँच की स्लैब के फ़लक पर किसी बिन्दु पर तिर्यक रुप से आपतित है। सामने वाले समान्तर फ़लक में से निकलने पर लाल और हरी किरणें निकलती हैं
View Solutionइनमें से कौन सा गोलीय लेन्स , परिक्षेपण प्रदर्शित नहीं करता ? लेन्सों के पृष्ठ के वक्रता व्यासार्ध चित्रों में दिए गए हैं
View Solutionलाल और बैंगनी रंगों की दो बीमें , अलग - अलग एक प्रिज़्म (जिसका कोण `60^(@)` है ) में से गुज़ारी जाती है। न्यूनतम विचलन स्थिति में अपवर्तन कोण होगा
View Solutionएक बल्ब एक दीवार पर है। इसी के आकार का इसका प्रतिबिम्ब एक उत्तल लेन्स की सहायता से एक समान्तर दीवार पर प्राप्त किया जाना है। लेन्स , दूसरी दीवार के सामने d दूरी पर रखा जाता है। तब अभीष्ट दूरी होगी
View Solutionएक लेन्स , प्रकाश के स्त्रोत और दीवार के बीच रखा जाता है। यह अपनी दो अलग - अलग स्थितियों के लिए दीवार पर `A_(1)` और `A_(2)` क्षेत्रफलों के प्रतिबिम्ब बनाता है। प्रकाश के स्त्रोत का क्षेत्रफल है
View Solution`+- 15 cm` और `+- 150 cm` फ़ोकस दूरियों के चार लेन्स , दूरदर्शक बनाने के लिए उपलब्ध हैं। अधिकतम आवर्धन उत्पन्न करने के लिए नेत्रिका की फ़ोकस दूरी होनी चाहिए
View Solutionएक समतल - उत्तल लेंस का व्यास 6 cm है और केन्द्र पर इसकी मोटाई 3 mm है। यदि लेन्स के पदार्थ में प्रकाश कि चाल `2 xx 10^(8) m//s` हो , तो लेन्स की फ़ोकस दूरी है
View Solutionयदि एक उत्तल लेन्स की संयुग्मी में `m_(1)` और `m_(2)` , पदार्थ के रेखीय आवर्धन हों और यदि d , संयुग्मी स्थितियों के बीच दूरी हो , तो लेन्स की फ़ोकस दूरी है
View Solutionएक अवतल दर्पण की फ़ोकस दूरी निकालने के लिए किए गए प्रयोग में u और v के परिमाण के बीच ग्राफ़ बनाया जाता है। ग्राफ़ ऐसा दिखता है
View Solutionएक समतल - उत्तल लेन्स के समतल पर चाँदी की परत चढ़ी हुई है। यदि `mu` , अपवर्तनांक हो और R , वक्र पृष्ठ का वक्रता व्यासार्ध , तो समूह एक अवतल दर्पण के रूप में व्यवहार करेगा जिसका वक्रता व्यासार्ध है
View Solution1.5 अपवर्तनांक और 30 cm वक्रता व्यासार्ध वाले एक समतल - उत्तल लेन्स के वक्र पृष्ठ पर चाँदी चढ़ी हुई है। अब इस लेन्स का प्रयोग एक वस्तु का प्रतिबिम्ब बनाने के लिए किया जाता है। इस लेन्स से कितनी दूरी पर एक वस्तु रखी जाए कि वस्तु के आकार का वास्तविक प्रतिबिम्ब प्राप्त हो ?
View Solutionग्राफ [चित्र VI.18] में एक समोत्तल लेन्स के लिए वस्तु की दूरी u और प्रतिबिम्ब की दूरी वके बीच सम्बन्ध दिखाया गया है। उत्तल लेन्स की फ़ोकस दूरी है
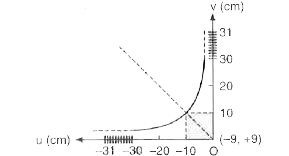
View Solutionअनन्त पर पड़ी वस्तु के 30 cm फ़ोकस दूरी वाले उत्तल लेन्स द्वारा बनाए गए प्रतिबिम्ब का आकार 2 cm है। यदि 20 cm फ़ोकस दूरी का अवतल लेन्स , उत्तल लेन्स और प्रतिबिम्ब के बीच , उत्तल लेन्स से 26 cm की दूरी पर रखी जाए , तो प्रतिबिम्ब का नया आकार निकालें।
View Solutionएक बिन्दु वस्तु , 15 cm फ़ोकस दूरी वाले पतले समतल उत्तल लेन्स से 20 cm की दूरी पर रखी जाती है। लेन्स के समतल पृष्ठ पर अब चाँदी की परत चढ़ा दी जाती है [चित्र VI.19]। सिस्टम द्वारा उत्पन्न प्रतिबिम्ब
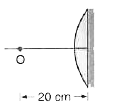
View Solution15 cm फ़ोकस दूरी वाला एक उभयोत्तल लेन्स , एक समतल सर्पण के सामने है। लेन्स और दर्पण के बीच दूरी 10 cm है। एक छोटी वस्तु , लेन्स से 30 cm की दूरी पर रखी जाती है। अन्तिम प्रतिबिम्ब है
View Solutionएक उत्तल लेन्स , किसी अवतल लेन्स के साथ सम्पर्क में है। उनकी फ़ोकस दूरियों के अनुपात का परिमाण `2//3` है। उनकी तुल्य फ़ोकस दूरी 30 cm है। उनकी अलग - अलग फ़ोकस दूरियाँ (cm) में क्या हैं ?
View Solutionहाइड्रोजन गैस , एक पारदर्शक गुब्बारे में भरी जाती है जिसे वायु में रखा जाता है। गुब्बारा इन जैसा व्यवहार करता है
View Solutionकाँच `(mu = 1.5)` का + 10 cm फ़ोकस दूरी वाला पतला लेन्स , जल `(mu = 1.33)` में डुबोया जाता है। नई फ़ोकस दूरी है
View Solutionएक प्रकाशिकी के प्रयोग में वस्तु की स्थिति स्थिर रखते हुए एक छात्र , उत्तल लेन्स की स्थिति परिवर्तित करता है और हर स्थिति के लिए वस्तु का स्फष्ट प्रतिबिम्ब प्राप्त करने के लिए परदे को समायोजित किया जाता है। लेन्स से वस्तु की दूरी u और प्रतिबिम्ब की दूरी v के बीच ग्राफ़ बनाया जाता है जिसमें दोनों अक्षों के लिए एक ही पैमाना प्रयुक्त किया जाता है। मूल बिन्दु से गुज़रती हुई और X - अक्ष के साथ `45^(@)` का कोण बनाती हुई एक सरल रेखा , प्रयोगिक वक्र को P पर मिलती है। P के निर्देशांक होंगे
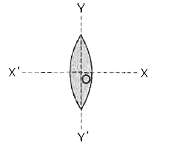
View Solutionएक समोत्तल लेन्स , चित्र VI. 20 में दिखाए अनुसार (i) X' OX और (ii) YOY' के अनुदिश दो अर्धभागों में काटा जाता है। मान लें कि पूर्ण लेन्स , परिस्थिति (i) में हर आधे भाग और परिस्थिति (ii) में हर आधे भाग की फ़ोकस दूरियाँ , क्रमशः f , f' और f'' हैं। निम्न में से सही कथन चुनें
View Solutionf फ़ोकस दूरी और d व्यास के द्वारक वाला लेन्स , I तीव्रता का प्रतिबिम्ब बनाता है। लेन्स के केन्द्रीय क्षेत्र में `d//2` व्यास का द्वारक अदीप्त कागज़ द्वारा ढक दिया जाता है। लेन्स की फ़ोकस दूरी और प्रतिबिम्ब की तीव्रता , क्रमशः , होंगे
View Solutionएक वस्तु , एक उत्तल लेन्स से x दूरी पर रखी जाती है। n गुना आवर्धित प्रतिबिम्ब प्राप्त करने के लिए आवश्यक लेन्स की क्षमता है
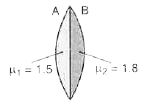
View Solutionएक उत्तल लेन्स दो अलग - अलग पदार्थों का बना है जिसमें फ़लक A का व्यासार्ध 25 cm और फ़लक B का 24 cm है। लेन्स की प्रभावी फ़ोकस दूरी [चित्र VI. 21] है
View Solutionएक संयुक्त सूक्ष्मदर्शी का आवर्धन 30 है। नेत्रिका की फ़ोकस दूरी 5 cm है और प्रतिबिम्ब , सुस्पष्ट दर्शन की 25 cm की दूरी पर बनाता है। अभिदृश्यक का आवर्धन है
View Solutionएक सूक्ष्मदर्शी के अभिदृश्यक और नेत्रिका लेंसों की फ़ोकस दूरियाँ क्रमशः 1.6 cm और 2.5 cm हैं। दोनों लेंसों के बीच दूरी 21.7 cm है। यदि अन्तिम प्रतिबिम्ब अनन्त पर बने , तो रेखीय आवर्धन क्या है ?
View Solutionसंयुक्त सक्ष्मदर्शी में मध्यवर्ती प्रतिबिम्ब है
View Solutionएक समतल उत्तल लेन्स , एक समतल - अवतल लेन्स में पूरी तरह समा जाता है उनके समतल पृष्ठ एक - दूसरे के समान्तर हैं। यदि लेन्स , `mu_(1)` तथा `mu^(2)` अपवर्तनांक वाले अलग - अलग पदार्थों के बने हों तथा उनके वक्र पृष्ठों का व्यासार्ध R हो , तो संयोजक की फ़ोकस दूरी है
View Solutionएक समतल उत्तल लेन्स द्वारा इसके 8 m पीछे की दूरी पर बना एक वस्तु का प्रतिबिम्ब , वास्तविक तथा वस्तु के साइज़ का एक - तिहाई हैं। लेन्स के अन्दर प्रकाश का तरंगदैर्ध्य , आकाश में तरंगदैध्य का `(2//3)` गुना है। लेन्स के वक्र पृष्ठ का व्यासार्ध है
View Solutionएक दूरदर्शक का अभिदृश्यक लेन्स , 200 cm फ़ोकस दूरी का है और नेत्रिका , 2 cm फ़ोकस दूरी का। यदि यह दूरदर्शक , 2 km दूरी पर 50 m ऊँची इमारत देखने के लिए प्रयुक्त किया जाए , तो अभिदृश्यक लेन्स द्वारा बने इमारत के प्रतिबिम्ब की ऊँचाई कितनी है ?
View Solution`+ 10 cm , + 50 cm , + 100 cm` और `+ 200 cm` फ़ोकस दूरियों वाले चार लेन्स , खगोलीय दूरदर्शक बनाने के लिए उपलब्ध हैं। अधिकतम आवर्धन उत्पन्न करने के लिए नेत्रिका की फ़ोकस दूरी होनी चाहिए
View Solutionसामान्य आँख का स्वच्छ पटल ,40 D की अभिसारी क्षमता उपलब्ध करवाता है और स्वच्छ पटल के पीछे आँख के लेन्स की न्यूनतम क्षमता 20 D है। इस सुचना को प्रयुक्त करते हुए दृष्टि पटल और स्वच्छ पटल के (आँख के ) लेन्स के बीच दूरी का यह अनुमान लगाया जा सकता है
View Solutionदस गुना कोणीय आवर्धन वाले एक खगोलीय दूरदर्शक की लम्बाई 44 cm है। अभिदृश्यक की फ़ोकस दूरी है
View Solution60 cm फ़ोकस दूरी के अभिदृश्यक और 5 cm फ़ोकस दूरी के नेत्रिका वाले दूरदर्शक को एक दूरस्थ वस्तु पर फ़ोकसित किया जाता है ताकि नेत्रिका से समान्तर किरणें निकालें। यदि वस्तु , अभिदृश्यक पर `2^(@)` का कोण बनाए , तो प्रतिबिम्ब की कोणीय चौड़ाई होगी
View Solutionएक कैमरे के लेन्स का द्वारक f है और उदभासन काल (exposure time ) `(1//60)`s है। यदि द्वारक 1.4 f हो जाए , तो न्य उदभासन काल क्या होगा ?
View Solutionएक प्रकाशिक तन्तु के वायु - क्रोड अन्तरापृष्ठ पर अधिकतम मान्य कोण कितने होंगे यदि क्रोड और परिनिधान अधिपट्टन (cladding ) के अपवर्तनांक क्रमशः `n_(1)` और `n_(2)` हों ?
View Solutionकोहरे में से देखा नहीं जा सकता क्योंकि
View Solutionनई बैटरियों वाले क्षणदीप (flashlight) से दीप्त श्वेत प्रकाश उत्पन्न होता है। ज्यों - ज्यों बैटरियाँ पुरानी होती है ,
View Solution`lamda` तरंगदैर्ध्य और `I_(0)` तीव्रता का प्रकाश , d मोटाई के एक पदार्थ में से गुज़रता है। परिणामी तीव्रता है
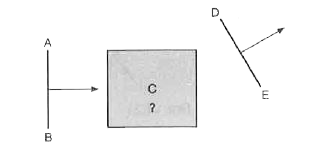
View Solutionचित्र VI. 22 में दर्शाए अनुसार एक तरंगाग्र AB , जो किसी समूह C से गुज़रता है , DE के रूप में निकलता है। सिस्टम हो सकता है
View Solutionयंग के द्विस्लिट प्रयोग में स्लिटें , जो एक - दूसरे से 2 mm की दूरी पर है , `lamda_(1) = 12000 Å` तथा `lamda_(2) = 10000 Å)` के दो तरंगदैर्ध्य के फ़ोटोनों द्वारा प्रदीप्त की जाती हैं। स्लिटों से 2 m दूर रखे परदे पर उभयनिष्ट केन्द्रीय दीप्त फ्रिन्ज से कितनी न्यूनतम दूरी पर एक व्यतिकरण पैटर्न से एक दीप्त फ्रिन्ज , दूसरे से दीप्त फ्रिन्ज के सम्पाती होगा ?
View Solutionएक व्यतिकरण कोष्ठ (interference chamber) में जब वायु थी , ते व्यतिकरण देखा गया। अब कोष्ठ को खाली कर दिया जाता है और वही प्रकाश प्रयुक्त किया गया जाता है। एक सावधान प्रेक्षक देखेगा
View Solutionएकल स्लिट विवर्तन पैटर्न में यदि केन्द्रीय उच्चिष्ठ की तीव्रता `I_(0)` हो , तो स्लिट की चौड़ाई दुगनी करने पर इसकी तीव्रता कितनी होगी ?
View SolutionI और 4I तीव्रताओं वाली प्रकाश की दो बीमों के व्यतिकरण से परदे पर फ्रिन्ज पैटर्न बनता है। दोनों बीमों के बीच कलान्तर , बिन्दु A पर `pi//2` है और बिन्दु B पर `pi ।` तब A और B पर परिणामी तीव्रताओं के बीच अन्तर है
View Solution1.5 अपवर्तनांक वाले पारदर्शक काँच की न्यूनतम मोटाई , जिस पर `lamda = 6000Å` की समतल प्रकाश तरंग परावर्तित होने पर उच्चिष्ठ प्रदर्शित करती है , हैं
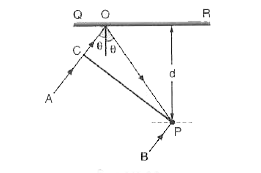
View Solutionचित्र VI. 23 में CP , एक तरंगाग्र प्रदर्शित करता है और AO तथा BP , संगत दो किरणें। किरण BP और परावर्तित किरण OP के बीच P पर संपोषी व्यतिकरण के लिए `theta` के लिए शर्त निकालें।
View Solutionसाबुन का एक बुलबुला , प्रेक्षक के निकटतम बिन्दु पर हरा `(lamda = 540 nm)` दिखता है। इसकी न्यूनतम मोटाई क्या है ? मान लें `uu = 135` है।
View Solutionयदि एक समतल काँच की प्लेट और एक उत्तल लेन्स के बीच पतली वायु की फिल्म , एकवर्णी प्रकाश की एक बीम द्वारा किरणित की जाए और किसी सूक्ष्मदर्शी के नीचे देखि जाए , तो आप देखेंगे
View Solutionआपस में 1 mm की दूरी पर दो स्लिटें , `65 xx 10^(-7)m` तरंगदैर्ध्य के प्रकाश द्वारा प्रदीप्त की जाती हैं। व्यतिकरण फ्रिन्ज , 1 m की दूरी पर रखे परदे पर देखे जाते है। तीसरे अदीप्त फ्रिन्ज और पाँचवें दीप्त फ्रिन्ज के बीच दूरी होगी
View Solutionयंग के द्विस्लिट प्रयोग में स्लिटों के बीच अन्तराल d है और प्रयुक्त प्रकाश का तरंगदैर्ध्य `6000 Å` है। यदि किसी दूरस्थ परदे पर बने फ्रिन्ज की कोणीय चौड़ाई `1^(@)` हो , तो d का मान है
View Solutionयंग के द्विस्लिट प्रयोग में स्लिटों के बीच अन्तराल 1 mm है और पर्दा स्लिटों से 1 m की दूर है। किसी 500 nm तरंगदैर्ध्य के एकवर्णी प्रकाश के लिए केन्द्रीय उच्चित से तीसरे निम्निष्ठ की दूरी है
View Solutionयंग के द्विस्लिट प्रयोग में दो स्त्रोतों के बीच दूरी 0.1 mm है। स्त्रोत से परदे की दूरी 20 cm है। प्रयुक्त किए गए प्रकाश का तरंगदैर्ध्य `5460 Å` है। तब पहले अदीप्त फ्रिन्ज की कोणीय स्थिति है
View Solutionयंग के द्विस्लिट प्रयोग में एकवर्णी प्रकाश का प्रयोग किया जाता है। परदे पर बने व्यतिकरण फ़्रिंजों का आकार है
View Solutionयंग के द्विस्लिट प्रयोग में तरंगदैर्ध्य से दुगने स्लिट अन्तराल के लिए व्यतिकरण उच्चिष्ठों की अधिकतम सम्भव संख्या है
View Solution
प्रतियोगिता सामग्री बहुविकल्पीय प्रश्न : एक सही विकल्प questions and complete solutions for chapter तरंग प्रकाशिकी of GRB PUBLICATIONS PHYSICS (HINDI) of Class 12
All Exercises from GRB PUBLICATION HINDI Class 12 PHYSICS तरंग प्रकाशिकी
- NCERT पाठ्यपुरस्तक अभ्यास:
- उच्चस्तरीय चितन: प्रश्नोत्तरी
- उदाहरण
- प्रतियोगिता सामग्री कथन-कारण -आधारित प्रश्न
- प्रतियोगिता सामग्री कॉलम मिलाये
- प्रतियोगिता सामग्री पूर्णक उत्तर वाले प्रश्न
- प्रतियोगिता सामग्री बहुविकल्पीय प्रश्न : एक सही विकल्प
- प्रतियोगिता सामग्री रिक्त स्थान भरना
- प्रतियोगिता सामग्री सत्य या असत्य
- प्रश्नोत्तरी 1 अंक
- प्रश्नोत्तरी 2 और 3 अंक
- प्रश्नोत्तरी 5 अंक
- विषय- आधारित समस्याएँ
- विषय: आधारित अभ्यास