Complete Solutions to प्रतियोगिता सामग्री (बहुविकल्पीय प्रश्न: एक या एक से अधिक सही विकल्प ) of chapter नाभिक of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | नाभिक |
| GRB PUBLICATION HINDI | प्रतियोगिता सामग्री (बहुविकल्पीय प्रश्न: एक या एक से अधिक सही विकल्प ) |
| Number Of Questions | 46 |
| Academic Year | 2023-24 |
एक हाइड्रोजन - जैसे परमाणु के एक इलेक्ट्रॉन की कक्षा का व्यासार्ध `4.5 a_0` है , जहाँ `a_0` बोर व्यासार्ध है। इसका कक्षीय कोणीय संवेग `(3h//2pi)` है। हमें दिया गया है कि h प्लांक स्थिरांक है और R रिडबर्ग स्थिरांक। जब परमाणु व्युत्तेजिट होता है तो संभव तंगदैर्ध्य है
View Solutionहाइड्रोजन के बोर मॉडल में,
View Solutionमान लें `A_n` कि एक हाइड्रोजन परमाणु की nवीं कक्षा द्वारा घिरा क्षेत्रफल निरूपित करता है। 1n `(A_n//A_1)` का ln n के साथ ग्राफ़
View Solutionकिसी हाइड्रोजन परमाणु में इलेक्ट्रॉन `n_1 rarr n_2` संक्रमण करता है जहाँ `n_1` और `n_2` दो अवस्थाओं की मुख्य क्वांटम संख्याएँ है। माना लें कि बोर मॉडल वैध है। आरम्भिक अवस्था में इलेक्ट्रॉन का आवर्त काल, अन्तिम अवस्था में इसके आवर्त काल से आठ गुना है। और `n_2` के सम्भव मान है
View Solutionएक ऐक्स - किरण ट्यूब को लगाया गया विभावान्तर बढ़ाया जाता है। परिणामस्वरूप उत्सर्जित विकरण में
View Solutionकिसी ऐक्स - किरण ट्यूब से आ रही ऐक्स - किरण बीम होगी
View Solutionएक ऐक्स - किरण ट्यूब से उत्सर्जित ऐक्स - किरणों का न्यूनतम तरंगदैर्घ्य पर निर्भर करता है
View Solutionएक नाभिक की द्रव्यमान संख्या होती है
View Solutionभारी नाभिकों की चेष्टा होती है कि उनका N/Z अनुपात बड़ा हो क्योंकि
View Solutionमान लें कि `m_p` प्रोटॉन का द्रव्यमान है, `m_n` न्यूट्रॉन का द्रव्यमान है , `M_1 , ""_(10)^(20)Ne` और `M_2,""_(20)^(40)Ca` नाभिक का द्रव्यमान है। तब
View Solutionज्यों - ज्यों द्रव्यमान संख्या A बढ़ती है नाभिक से सम्बन्धित इनमें से कौन - सी राशि नहीं बदलती ?
View Solutionइनमें से कौन सा / से कथन सत्य है/ हैं ?
View Solutionनाभिकीय विखंडन अभिक्रिया के दौरान
View Solutionऋणात्मक बीटा - क्षय में
View Solutionनिम्न क्षयो में से किस में परमाणविक संख्या घटती है ?
View Solution`""^(131)I` की अर्ध - आयु 8 दिन है| जब t = 0 समय पर `""^(131)I` नमूना दिया गया हो , तो हम निश्चयपूर्वक कह सकते हैं कि
View Solutionएक मुक्त न्यूट्रॉन पर प्रोटॉन के रूप में क्षय होता हैं परन्तु एक मुक्त प्रोटॉन का न्यूट्रॉन के रूप में क्षय नहीं होता क्योंकि
View Solutionएक रेडियोसक्रिय नमूने का क्षय स्थिरांक `lamda` है नमूने की अर्ध - आयु और औसत आयु क्रमशः हैं
View Solution2 h अर्ध - आयु का एक ताज़ा - ताज़ा बना रेडियोसक्रिय स्त्रोत , अनुमत सुरक्षा के स्तर से 64 गुना तीव्रता का विकिरण उत्सर्जित करता है। न्यूनतम समय जिसके बाद इस स्त्रोत के साथ कार्य करना सुरक्षित होगा है
View Solutionएक रेडियोसक्रिय तत्व X का अर्थ - आयु समय वही है जो एक - दूसरे रेडियोसक्रिय तत्व Y का औसत - आयु समय है शुरू में दोनों में परमाणुओं की संख्या समान है तब
View Solutionमान लें कि न्यूक्लिऑन नाभिकीय बंधन ऊर्जा B/A का द्रव्यमान संख्या A के साथ ग्राफ चित्र में दिखाया अनुसार है |
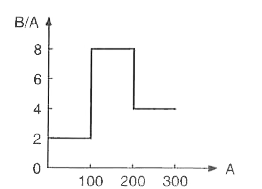
इस ग्राफ़ का प्रयोग करते हुए नीचे दिए गए विकल्प (विकल्पों) को चुने :
View Solution`A gt 100` वाले नाभिकों के लिए
View Solutionनिम्न समीकरणों में से संभव नाभिकीय संलयन अभिक्रियाएँ चुने :
View Solutionकिसी तारे में आरम्भ में `10^(40)`ड्यूट्रॉन है यदि निम्न प्रक्रिया के माध्यम से उर्जा उत्पन्न करता है :
`""_1^2H+""_1^2Hrarr""_1^3H+p` और `""_1^2H+""_1^3Hrarr""_2^4H+n`
यदि तारे द्वारा उत्सर्जित औसत शक्ति `10^6W` हो , तो तारे की ड्यूट्रॉन सप्लाई इस कोटि के समय में समाप्त हो जाती है
(नाभिकों के द्रव्यमान इस प्रकार हैं : :
`M(""_1^2H)=2.014u,M(p)=1.007u`,
`M(n)=1.008u, M(""_2^4He)=4.001u)`
View Solutionहाइड्रोजन परमाणु के स्पेक्ट्रम के बोर सिद्धांत की मुख्य विशेषता कोणीय संवेग का मेकरण है जब यह इलेक्ट्रॉन , प्रोटोन के गिर्द घूमता है। इसे सामान्य घूर्णन गति पर लगाएगे ताकि एक दिपरमानुक अनु को कठोर मानते हुए इसकी क्वान्तमित घूर्णन ऊर्जा निकाल सकें। लगाया जाने वाला नियम, बोर की क्वाण्टमीकरण शर्त है ।
एक द्विपरमाणुक अणु का जड़त्व आघूर्ण I है । बोर की क्वान्टमीकरण शर्त से n वें (n = 0 अनुमत नहीं है ) स्तर में इसकी घूर्णन ऊर्जा है
View Solutionहाइड्रोजन परमाणु के स्पेक्ट्रम के बोर सिद्धांत की मुख्य विशेषता कोणीय संवेग का मेकरण है जब यह इलेक्ट्रॉन , प्रोटोन के गिर्द घूमता है। इसे सामान्य घूर्णन गति पर लगाएगे ताकि एक दिपरमानुक अनु को कठोर मानते हुए इसकी क्वान्तमित घूर्णन ऊर्जा निकाल सकें। लगाया जाने वाला नियम, बोर की क्वाण्टमीकरण शर्त है ।
यह पाया गया है कि CO अणु के लिए निम्नतम अवस्था से प्रथम उत्तेजित घूर्णन अवस्था तक उत्तेजन आवृत्ति , `(4//pi)xx10^(11)Hz` निकट है | CO अणु का अपने द्रव्यमान केन्द्र के गिर्द जड़त्व आघूर्ण इनके निकट है
`(h = 2pi xx10^(-34)Js` लें )
View Solutionहाइड्रोजन परमाणु के स्पेक्ट्रम के बोर सिद्धांत की मुख्य विशेषता कोणीय संवेग का मेकरण है जब यह इलेक्ट्रॉन , प्रोटोन के गिर्द घूमता है। इसे सामान्य घूर्णन गति पर लगाएगे ताकि एक दिपरमानुक अनु को कठोर मानते हुए इसकी क्वान्तमित घूर्णन ऊर्जा निकाल सकें। लगाया जाने वाला नियम, बोर की क्वाण्टमीकरण शर्त है ।
एक अणु में C (द्रव्यमान = 12 amu ) और O (द्रव्यमान = 16 amu ), जहाँ 1 amu `=(5//3)xx10^(-27)kg` है बीच डोरी इनके निकट है।
View Solution` H - He ^(+)` गैस ( `He^(+)` एक एकधा आयनित He परमाणु है ) के मिश्रण में H परमाणु और `He^(+)` ऑयन अपनी प्रथम उत्तेजित अवस्थाओं तक उत्तेजित किया जाते है। H बाद में परमाणु अपनी सारी उत्तेजना ऊर्जा `He^(+)` आयनों को टक्करों द्वारा दे देते हैं। मान ले कि बोर का परमाणु मॉडल यथार्थ रूप में वैध है |
उपरोक्त की सहायता से निम्न प्रश्न में सबसे उपरोक्त उत्तर चुने:
`He^(+)` आयनों में अन्त तक पहुँची अवस्था की क्वार्टर संख्या n यह है
View Solution` H - He ^(+)` गैस ( `He^(+)` एक एकधा आयनित He परमाणु है ) के मिश्रण में H परमाणु और `He^(+)` ऑयन अपनी प्रथम उत्तेजित अवस्थाओं तक उत्तेजित किया जाते है। H बाद में परमाणु अपनी सारी उत्तेजना ऊर्जा `He^(+)` आयनों को टक्करों द्वारा दे देते हैं। मान ले कि बोर का परमाणु मॉडल यथार्थ रूप में वैध है |
उपरोक्त की सहायता से निम्न प्रश्न में सबसे उपरोक्त उत्तर चुने:
H परमाणुओं के साथ टक्करों के बाद `He^(+)` आयनों द्वारा दृश्य क्षेत्र में उत्सर्जित प्रकाश का तरंगदैर्ध्य यह है
View Solution` H - He ^(+)` गैस ( `He^(+)` एक एकधा आयनित He परमाणु है ) के मिश्रण में H परमाणु और `He^(+)` ऑयन अपनी प्रथम उत्तेजित अवस्थाओं तक उत्तेजित किया जाते है। H बाद में परमाणु अपनी सारी उत्तेजना ऊर्जा `He^(+)` आयनों को टक्करों द्वारा दे देते हैं। मान ले कि बोर का परमाणु मॉडल यथार्थ रूप में वैध है |
उपरोक्त की सहायता से निम्न प्रश्न में सबसे उपरोक्त उत्तर चुने:
H परमाणु की n = 2 इलेक्ट्रॉन की गतिज ऊर्जा और `He^(+)` परमाणु की n= 2 इलेक्ट्रॉन की गतिज ऊर्जा का अनुपात यह है
View Solutionएक नाभिक X, आरम्भ में विराम अवस्था में है। इसमें समीकरण `""_(92)^AX rarr ^(238)Y_z+alpha` के अनुसार ऐल्फ़ा - क्षय होता हैं। इस क्षय में उत्पन्न ऐल्फ़ा - कण , एकसमान चुंबकीय क्षेत्र B में r व्यासार्ध की एक वृत्ताकार का लीक में चलता है। हमें दिया गया है कि
`m(Y) = 228.3u , m(""_0^1n)=1.009u,m(""_2^4He)=4.003u`,
`m(""_1^1H)=1.008u, r - 0.11 m ` और B = 3T हैं।
उपरोक्त की सहायता से निम्न प्रश्नों से सबसे उपयुक्त उत्तर चुने:
ऐल्फ़ा - कण की गतिज ऊर्जा (MeV) में लगभग यह है
View Solutionएक नाभिक X, आरम्भ में विराम अवस्था में है। इसमें समीकरण `""_(92)^AX rarr ^(238)Y_z+alpha` के अनुसार ऐल्फ़ा - क्षय होता हैं। इस क्षय में उत्पन्न ऐल्फ़ा - कण , एकसमान चुंबकीय क्षेत्र B में r व्यासार्ध की एक वृत्ताकार का लीक में चलता है। हमें दिया गया है कि
`m(Y) = 228.3u , m(""_0^1n)=1.009u,m(""_2^4He)=4.003u`,
`m(""_1^1H)=1.008u, r - 0.11 m ` और B = 3T हैं।
उपरोक्त की सहायता से निम्न प्रश्नों से सबसे उपयुक्त उत्तर चुने:
ऐल्फ़ा - क्षय की प्रक्रिया में कुल मोचित ऊर्जा (MeV) में यह है
View Solutionएक नाभिक X, आरम्भ में विराम अवस्था में है। इसमें समीकरण `""_(92)^AX rarr ^(238)Y_z+alpha` के अनुसार ऐल्फ़ा - क्षय होता हैं। इस क्षय में उत्पन्न ऐल्फ़ा - कण , एकसमान चुंबकीय क्षेत्र B में r व्यासार्ध की एक वृत्ताकार का लीक में चलता है। हमें दिया गया है कि
`m(Y) = 228.3u , m(""_0^1n)=1.009u,m(""_2^4He)=4.003u`,
`m(""_1^1H)=1.008u, r - 0.11 m ` और B = 3T हैं।
उपरोक्त की सहायता से निम्न प्रश्नों से सबसे उपयुक्त उत्तर चुने:
मूल नाभिक की प्रति न्युक्लियऑन बंधन ऊर्जा (MeV) में यह हैं
View Solution`M+Deltam` द्रव्यमान का एक नाभिक , विराम अवस्था में है और इसका M/2 के समान द्रव्यमान दो संतति नाभिकों के रूप में क्षय हो जाता है। प्रकाश की चाल c है
संतति नाभिक की चाल है।
View Solution`M+Deltam` द्रव्यमान का एक नाभिक , विराम अवस्था में है और इसका M/2 के समान द्रव्यमान दो संतति नाभिकों के रूप में क्षय हो जाता है। प्रकाश की चाल c है
मूल नाभिक के लिए प्रति न्यूक्लिऑन बंधन ऊर्जा `E_1` और संतति नाभिक के लिए `E_2` हैं। तब
View Solutionमान लें आप को लकड़ी एक टुकड़ा मिला है। जो अत्यन्त प्राचीन माना जाता है। इस टुकड़े का भार 40 g है और यह 280 विघटन प्रति मिनट की सक्रियता दर्शाता है। एक जीवित पौधा , प्रति ग्राम 12 विघटन प्रति मिनट की `""^(14)C` सक्रियता दर्शाता है। `""^(14)C` की अर्ध - आयु 5730 वर्ष है
उपरोक्त की सहायता से निम्न प्रश्नों के सबसे उपयुक्त उत्तर चुने:
लकड़ी उस वृक्ष का हिस्सा थी जो लगभग इस समय काटा गया
View Solutionमान लें आप को लकड़ी एक टुकड़ा मिला है। जो अत्यन्त प्राचीन माना जाता है। इस टुकड़े का भार 40 g है और यह 280 विघटन प्रति मिनट की सक्रियता दर्शाता है। एक जीवित पौधा , प्रति ग्राम 12 विघटन प्रति मिनट की `""^(14)C` सक्रियता दर्शाता है। `""^(14)C` की अर्ध - आयु 5730 वर्ष है
उपरोक्त की सहायता से निम्न प्रश्नों के सबसे उपयुक्त उत्तर चुने:
यदि लकड़ी का टुकड़ा वर्ष पुराना होता , तो इस की सक्रियता यह होती
View Solution`""_6^(11)C` का परमाणविक द्रव्यमान लगभग 11.0 g है और इसलिए `""_6^(11)C` के 11.0 g में नाभिकों की , आवोगाद्रो संख्या `(6.023xx10^(23))` , संख्या हैं। एक रेडियोसक्रिय नमूने में `3.50 mug` है शुद्ध `""_6^(11)C` हैं जिसकी अर्ध - आयु 20.4 मिनट है
उपरोक्त की सहायता से निम्न प्रश्नों के सबसे उपयुक्त उत्तर चुनें :
आरम्भ में नमूने , की सक्रियता (dps) में यह हैं |
View Solution`""_6^(11)C` का परमाणविक द्रव्यमान लगभग 11.0 g है और इसलिए `""_6^(11)C` के 11.0 g में नाभिकों की आवोगाद्रो संख्या `(6.023xx10^(23))` , संख्या हैं। एक रेडियोसक्रिय नमूने में `3.50 mug` है शुद्ध `""_6^(11)C` हैं जिसकी अर्ध - आयु 20.4 मिनट है
उपरोक्त की सहायता से निम्न प्रश्नों के सबसे उपयुक्त उत्तर चुनें :
8.00 h के बाद नमूने की सक्रियता (क्षय / सेकण्ड में ) यह है
View Solution`""_6^(11)C` का परमाणविक द्रव्यमान लगभग 11.0 g है और इसलिए `""_6^(11)C` के 11.0 g में नाभिकों की आवोगाद्रो संख्या `(6.023xx10^(23))` , संख्या हैं। एक रेडियोसक्रिय नमूने में `3.50 mug` है शुद्ध `""_6^(11)C` हैं जिसकी अर्ध - आयु 20.4 मिनट है
उपरोक्त की सहायता से निम्न प्रश्नों के सबसे उपयुक्त उत्तर चुनें :
8.00 h के बाद बच्चे रेडियोसक्रिय नाभिकों की संख्या यह है
View Solutionवैज्ञानिक कड़ी मेहनत से नाभिकीय संलयन रिएक्टर विकसित करने में लगे हैं | भारी हाइड्रोजन नाभिक `""_(1)^(2)H,` जिसे ड्यूट्रॉन कहते हैं और D से दर्शाते हैं, संलयन - रिएक्टर के लिए संभावना के रूप में सोचा जा सकता है | D-D अभिक्रिया है, `""_(1)^(2)H+""_(1)^(2)Hrarr ""_(2)^(3)He+n+` ऊर्जा | संलयन - रिएक्टर के कोर में भारी हाइड्रोजन गैस, ड्यूट्रॉन नाभिकों और इलेक्ट्रॉनों में पूर्णतया आयनित हो जाती है | इन `""_(1)^(2)H` नाभिकों और इलेक्ट्रॉनों के समूह को प्लाज्मा कहते हैं | रिएक्टर कोर में नाभिक यादृच्छिक गति करते हैं और यदा-कदा इतने पास आ जाते हैं कि नाभिकीय संलयन हो सके | सामान्यतया, रिएक्टर कोर में तापमान बहुत अधिक होता है और इस कारण किसी भी पदार्थ की दीवार इस प्लाज्मा को अपने अन्दर परिसीमित रखने में सक्षम नहीं हो पाती | इसलिये विशेष तकनीकों का प्रयोग करके इस प्लाज्मा को कुछ समय तक परिसीमित किया जाता है, इससे पहले कि कण कोर से दूर चले जायें | यदि n ड्यूट्रॉनों का घनत्व `("संख्या//आयतन")` हो तथा `t_(0)` परिसीमन समय हो तो `nt_(0)` को लॉसन नम्बर कहते हैं | एक मानक के अनुसार किसी रिएक्टर को सफल करने के लिए लॉसन नम्बर का मान `5xx10^(14)s//cm^(3)` से अधिक होना चाहिए |
नीचे दिये गये स्थिरांकों का प्रयोग आपके लिये उपयोगी हो सकता है | वोल्ट्समान नियतांक : `k=8.6xx10^(-5)eV//K,`
`(e^(2))/(4pi epsilon_(0))=1.44xx10^(-9)eVm`.
नाभिकीय संलयन-रिएक्टर कोर में गैस से प्लाज्मा बनने का कारण है
View Solutionवैज्ञानिक कड़ी मेहनत से नाभिकीय संलयन रिएक्टर विकसित करने में लगे हैं | भारी हाइड्रोजन नाभिक `""_(1)^(2)H,` जिसे ड्यूट्रॉन कहते हैं और D से दर्शाते हैं, संलयन - रिएक्टर के लिए संभावना के रूप में सोचा जा सकता है | D-D अभिक्रिया है, `""_(1)^(2)H+""_(1)^(2)Hrarr ""_(2)^(3)He+n+` ऊर्जा | संलयन - रिएक्टर के कोर में भारी हाइड्रोजन गैस, ड्यूट्रॉन नाभिकों और इलेक्ट्रॉनों में पूर्णतया आयनित हो जाती है | इन `""_(1)^(2)H` नाभिकों और इलेक्ट्रॉनों के समूह को प्लाज्मा कहते हैं | रिएक्टर कोर में नाभिक यादृच्छिक गति करते हैं और यदा-कदा इतने पास आ जाते हैं कि नाभिकीय संलयन हो सके | सामान्यतया, रिएक्टर कोर में तापमान बहुत अधिक होता है और इस कारण किसी भी पदार्थ की दीवार इस प्लाज्मा को अपने अन्दर परिसीमित रखने में सक्षम नहीं हो पाती | इसलिये विशेष तकनीकों का प्रयोग करके इस प्लाज्मा को कुछ समय तक परिसीमित किया जाता है, इससे पहले कि कण कोर से दूर चले जायें | यदि n ड्यूट्रॉनों का घनत्व `("संख्या//आयतन")` हो तथा `t_(0)` परिसीमन समय हो तो `nt_(0)` को लॉसन नम्बर कहते हैं | एक मानक के अनुसार किसी रिएक्टर को सफल करने के लिए लॉसन नम्बर का मान `5xx10^(14)s//cm^(3)` से अधिक होना चाहिए |
नीचे दिये गये स्थिरांकों का प्रयोग आपके लिये उपयोगी हो सकता है | वोल्ट्समान नियतांक : `k=8.6xx10^(-5)eV//K,`
`(e^(2))/(4pi epsilon_(0))=1.44xx10^(-9)eVm`.
मान लें कि संलयन रिएक्टर कोर में, जिसका तापमान T है, दो ड्यूट्रॉन एक दूसरे की तरफ बढ़ रहे हैं, प्रत्येक की गतिज ऊर्जा 1.5kT है और उनकी आपसी दूरी इतनी ज्यादा है कि उनके बीच कूलाम विभव ऊर्जा को नगण्य मान सकते हैं | कोर में उपस्थित दूसरे कणों के साथ इन दोनों की किसी प्रकार की आपसी क्रिया को भी नगण्य मान सकते हैं | ये ड्यूट्रॉन `4xx10^(-15)m` की दूरी तक पहुँच पायें इसके लिए आवश्यक न्यूनतम तापमान T होगा इस अन्तराल में
View Solutionवैज्ञानिक कड़ी मेहनत से नाभिकीय संलयन रिएक्टर विकसित करने में लगे है। भारी हाइड्रोजन नाभिक `""_1^2H`, जिसे पॅट्रॉन कहते है और D से दर्शाते है। संलयन रिएक्टर के लिये संभावना के रूप में प्रयोग किया जा सकता है। D - D अभिक्रिया है: `""_1^2H + ""_1^2H to ""_2^3 He + n+` ऊर्जा, संलयन रिएक्टर के कोर में भारी हाइड्रोजन गैस, ड्यूट्रॉन नाभिको और इलेक्ट्रॉनों में पूर्णतया आयनित हो जाती है। इन `""_1^2H` नाभिको और इलेक्ट्रॉनों के समूह को प्लाज्मा कहते है। रिएक्टर कोर में नाभिकीय संलयन हो सके। सामान्यता, रिएक्टर कोर में तापमान बहुत बहुत अधिक होता है और इस कारण किसी भी पदार्थ की दीवार इस प्लाज्मा को अपने अन्दर परिसीमित रखने में सक्षम नहीं हो पाती है। इसलिये विशेषज्ञ तकनीको का प्रयोग करके इस प्लाज्मा को कुछ समय तक परिसीमित किया जाता है। इससे पहले कि कण कोर से दूर चले जायें। यदि n ड्यूट्रॉनों का घनत्व (संख्या/आयतन) हो तथा `t_0` परिसीमन समय हो, तो `nt_0` को लासन नम्बर (Lawson number) कहते है।
यदि मानक के अनुसार किसी रिएक्टर को सफल करने के लिये लासन नम्बर का मान `5 xx 10^14 s//cm^3` से अधिक होना चाहिये। नीचे दिये गये स्थिरांको का प्रयोग आपके लिये उपयोगी हो सकता है।
वोल्ट्समान नियतांक `k =8.6 xx 10^(-5) eV//K , e^2/(4 pi epsi_0) = 1.44 xx 10^(-9) eVm`.
D - D अभिक्रिया के प्रयोग से बन सकने वाले संलयन रिएक्टर के चार सम्भावित प्रारूपों के लिये की गई गणना के परिणाम नीचे दिये गये है। लासन मानक के अनुसार इन चारों में से कौन सफलता का सबसे सशन्त प्रारूप है?
View Solutionजब एक कण को X - क्षय के अनुदिश x = 0 और x = a के बीच चलने के लिए प्रतिबंधित किया जाता है , जहाँ a, नैनोमीटर विमा का है , तो इसकी ऊर्जा के केवल कुछ विशिष्ट मान ही हो सकते हैं। ऐसे प्रतिबिंब क्षेत्र में चल रहे कण की अनुमत ऊर्जाऍं , अप्रगामि तरंगों की रचना के संगत होती है जिनके नोड इसके सिरों x = 0 और x = a पर है। इस अप्रगामि तरंग का तरंगदैर्ध्य , कण के रेखीय संवेग p के साथ दे ब्रॉग्ली सम्बन्ध के अनुसार सम्बन्धित है। m द्रव्यमान वाले कण की ऊर्जा, इसके रेखीय संवेग के साथ `E = p^2/(2m)` के अनुसार सम्बन्धित है। इस प्रकार कारण ऊर्जा एक , क्वान्टम संख्या n द्वारा निर्दिष्ट की जा सकती है जिसमें n के मान 1,2,3,..............(n =1 को निम्नतम अवस्था कहते हैं होते हैं जो अप्रगामी तरंग में लूपों की संख्या के संगत होते हैं।
उपरोक्त वर्णित मॉडल का प्रयोग, रेखा x = 0 से x = a में चल रहे कल के लिए निम्न तीन प्रश्नों के उत्तर देने के लिए करें |
`h= 6.6 xx10^(-34)Js` और `e = 1.6xx10^(-19)C` लें |
कण के लिए n के किसी विशेष मान के लिए अनुमत ऊर्जा अनुपाती है
View Solutionजब एक कण को X - क्षय के अनुदिश x = 0 और x = a के बीच चलने के लिए प्रतिबंधित किया जाता है , जहाँ a, नैनोमीटर विमा का है , तो इसकी ऊर्जा के केवल कुछ विशिष्ट मान ही हो सकते हैं। ऐसे प्रतिबिंब क्षेत्र में चल रहे कण की अनुमत ऊर्जाऍं , अप्रगामि तरंगों की रचना के संगत होती है जिनके नोड इसके सिरों x = 0 और x = a पर है। इस अप्रगामि तरंग का तरंगदैर्ध्य , कण के रेखीय संवेग p के साथ दे ब्रॉग्ली सम्बन्ध के अनुसार सम्बन्धित है। m द्रव्यमान वाले कण की ऊर्जा, इसके रेखीय संवेग के साथ `E = p^2/(2m)` के अनुसार सम्बन्धित है। इस प्रकार कारण ऊर्जा एक , क्वान्टम संख्या n द्वारा निर्दिष्ट की जा सकती है जिसमें n के मान 1,2,3,..............(n =1 को निम्नतम अवस्था कहते हैं होते हैं जो अप्रगामी तरंग में लूपों की संख्या के संगत होते हैं।
उपरोक्त वर्णित मॉडल का प्रयोग, रेखा x = 0 से x = a में चल रहे कल के लिए निम्न तीन प्रश्नों के उत्तर देने के लिए करें |
`h= 6.6 xx10^(-34)Js` और `e = 1.6xx10^(-19)C` लें |
यदि करण का द्रव्यमान `m = 1.0xx10^(-30)kg ` हो और a = 6.6 nm`, तो निम्नत अवस्था में कण की उर्जा इनकी निकटतम है
View Solutionजब एक कण को X - क्षय के अनुदिश x = 0 और x = a के बीच चलने के लिए प्रतिबंधित किया जाता है , जहाँ a, नैनोमीटर विमा का है , तो इसकी ऊर्जा के केवल कुछ विशिष्ट मान ही हो सकते हैं। ऐसे प्रतिबिंब क्षेत्र में चल रहे कण की अनुमत ऊर्जाऍं , अप्रगामि तरंगों की रचना के संगत होती है जिनके नोड इसके सिरों x = 0 और x = a पर है। इस अप्रगामि तरंग का तरंगदैर्ध्य , कण के रेखीय संवेग p के साथ दे ब्रॉग्ली सम्बन्ध के अनुसार सम्बन्धित है। m द्रव्यमान वाले कण की ऊर्जा, इसके रेखीय संवेग के साथ `E = p^2/(2m)` के अनुसार सम्बन्धित है। इस प्रकार कारण ऊर्जा एक , क्वान्टम संख्या n द्वारा निर्दिष्ट की जा सकती है जिसमें n के मान 1,2,3,..............(n =1 को निम्नतम अवस्था कहते हैं होते हैं जो अप्रगामी तरंग में लूपों की संख्या के संगत होते हैं।
उपरोक्त वर्णित मॉडल का प्रयोग, रेखा x = 0 से x = a में चल रहे कल के लिए निम्न तीन प्रश्नों के उत्तर देने के लिए करें |
`h= 6.6 xx10^(-34)Js` और `e = 1.6xx10^(-19)C` लें |
कण की चाल , जिसके विविक्त मान हो सकते हैं , इसके अनूपाती है
View Solution
प्रतियोगिता सामग्री (बहुविकल्पीय प्रश्न: एक या एक से अधिक सही विकल्प ) questions and complete solutions for chapter नाभिक of GRB PUBLICATIONS PHYSICS (HINDI) of Class 12
All Exercises from GRB PUBLICATION HINDI Class 12 PHYSICS नाभिक
- NCERT पाठ्यपुस्तक अभ्यास : उत्तरों सहित
- उच्चस्तरीय चिंतन : प्रश्नोत्तरी
- उदाहरण
- प्रतियोगिता सामग्री (कथन - कारण - आधारित प्रश्न )
- प्रतियोगिता सामग्री (कॉलम मिलाना)
- प्रतियोगिता सामग्री (पूर्णांक उत्तर वाले प्रश्न )
- प्रतियोगिता सामग्री (बहुविकल्पीय प्रश्न: एक या एक से अधिक सही विकल्प )
- प्रतियोगिता सामग्री (बहुविकल्पीय प्रश्न: एक सही विकल्प )
- प्रतियोगिता सामग्री (रिक्त स्थान भरना )
- प्रतियोगिता सामग्री (सत्य या असत्य )
- प्रश्नोत्तरी : 1 अंक
- प्रश्नोत्तरी : 2 और 3 अंक
- प्रश्नोत्तरी : 5 अंक
- विषय - आधारित अभ्यास ( रेडियोसक्रिय क्षय नियम , अर्ध - आयु ,औसत आयु )
- विषय - आधारित अभ्यास (नाभिक के गुण)
- विषय - आधारित अभ्यास (नाभिकीय अभिक्रियाएँ, विखंडन और संलयन)
- विषय - आधारित अभ्यास (प्रतिरूपी अभ्यास)
- विषय - आधारित समस्याएँ : हल सहित (नाभिक के गुण )
- विषय - आधारित समस्याएँ : हल सहित (नाभिकीय अभिक्रियाऍं , विखंडन और संलयन)
- विषय - आधारित समस्याएँ : हल सहित (रेडियोसक्रिय क्षय नियम , अर्ध - आयु औसत आयु )