Complete Solutions to QUESTION BANK of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| HIMALAYA PUBLICATION | QUESTION BANK |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Out of 30 consecutive numbers, 2 are chosen at random. The probability that their sum is odd, is
View SolutionTwo cards are drawn from a well shuffled pack of 52 cards. The probability that one is a spade and the other is heart, is
View SolutionSix unbiased coins are tossed. The probability of getting atleast 4 heads is
View SolutionTwo dice are rolled simultaneously. The probability that the sum of the two numbers ofn the dice is a prime number is
View SolutionIf A and B are events such that P(A) = 0.4, `P(A cup B) = 0.7`. If A and B are independent then P(B) =
View SolutionIf X is a random variable with distibution given below Then k = and variance =

View SolutionIn an experiment the success is twice that of failure. If the experiment is repeated 6 times, the probability that atleast 4 times favourable is
View SolutionTwo students work independently on a problem. The probability that the first one will solve it is 3/4 and the probability that the second one will solve it is 2/3. The probability that the problem is solved is
View SolutionThe probability of choosing at random a number that is divisible by 6 or 8 from among 1 to 90 is
View SolutionThe key for a door is in a bunch of 10 keys. A man attempts to open the door by trying keys at random discording the wrong key. The probability that the door is opened in the fifth trial is
View SolutionChoose the correct answer
If `P(A)=(1)/(2)`, P(B) = 0, then P(A|B) is
View SolutionChoose the correct answer
If A and B are events such that P(A|B) = P(B|A), then
View SolutionChoose the correct answer
The probability of obtaining an even prime number on each die, when a pair of dice is rolled is
View SolutionTwo events A and B will be independent if
View SolutionProbability that A speaks truth is 4/5. A coin is tossed. A reports that a head appears. The probability that actually there was head is
View SolutionIf A and B are two events such that `A sub B` and `P(B) ne 0`, then which of the following is correct?
View SolutionChoose the correct answer
The mean of the numbers obtained on throwing a die having written 1 on three faces, 2 on two faces and 5 on one face is
View SolutionChoose the correct answer
Suppose that two cards are drawn at random from a deck of cards. Let X be the number of aces obtained. Then the value of E(X) is
View SolutionChoose the correct answer:
In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is
View SolutionChoose the correct answer:
The probability that a student is not a swimmer is `(1)/(5)` out of five students, four are swimmers is
View SolutionChoose the correct answer:
If A and B are two events such that `P(A) != 0` and P(B|A) = 1, then
View SolutionChoose the correct answer:
If `P(A|B) gt P(A)`, then which of the following is correct :
View SolutionChoose the correct answer:
If A and B are any two events such that P(A) + P(B) - P(A and B) = P(A), then
View SolutionLet A and B be two events such that P(A) = 0.6, P(B) = 0.2 and P(A/B) = 0.5 then `P(A^(')/B^('))` equals
View SolutionIf A and B are independent events such that 0 < P(A) < 1 and 0 < P(B) < 1, then which of the following is not correct?
View SolutionLet X be a discrete random variable. The probability distribution of X is given below : Then E(X) equal to
View SolutionLet X be a distance random variable assuming values `x_(1),x_(2) ,…….,x_(n)` with probabilities `p_(1),p_(2)…..p_(n) `respectively . The variance of X is given by :
View SolutionLet A and B be two events .If P(A) = = 0.2 P(B) 0.4 ,`P(A cup B)=0.6` then P(A/B) is equal to :
View SolutionIf P(A) =4/5 and `P(A cap B)` = 7/10 then P(B/A) =
View SolutionIf P(A cap B) = 7/10 and P(B) = 17/20 then P(A/B) =
View SolutionIf P(A) = 3/10, P(B) = 2/5 and `P(A cup B ) = 3/5`, then P(B/A) + P(A/B) =
View SolutionIf P(A) = 2/5, P(B) = 3/10 and `P( A cap B )= 1/5` then, `P(A^(') |B^(')). P(B^(')|A^(')) = `
View SolutionIf A and B are two events such that P(A) = 1/2, P(B) = 1/3, P(A|B) = 1/4, then `P(A^(') cap B^(')) = `
View SolutionIf P(A) = 0.4, P(B) = 0.8 and P(B|A) = 0.6 then `P(A cup B) =`
View SolutionIf A and B are two events and `A ne phi, B ne phi` then
View SolutionA and B are events such that P(A) = 0.4, P(B) = 0.3 and `P( A cup B) = 0.5`. Then `P(B^(') cap A^(')) =`
View SolutionYou are given that A and B are two events such that P(B) = 3/5 and P(A|B) = 1/2 and `P(A cup B) = 4/5` then P(A) =
View SolutionYou are given that A and B are two events such that P(B) = 3/5, P(A|B) =1/2, P(A) =1/2 then `P(B|A)^(')) =`
View SolutionIf P(A) = 7/13, P(B) = 9/13 and `P(A cap B)= 4/13`. Then `P(A^(')|B) =`
View SolutionIf `P(A)= (7)/(13), P(B)= (9)/(13)` and `P(AnnB)= (4)/(13)` find `P(A//B)`
View SolutionIf A and B are such events that `P(A) gt 0, and `P(B) ne 1, then `P(A^(')|B^(')) =`
View SolutionIf A and B are two independent events with P(A) = 3/5 and P(B) = 4/9 then `P(A^(') cap B^(')) =`
View SolutionThree person A, B and C fire at a target, inturn starting. with A. Their probability of hitting the target are 0.4,0.3 and 0.2 respectively The probability of two hits is
View SolutionIf two events are independent, then
View SolutionLet A and B two events such that P(A) = 3/8, P(B) = 5/8 and `P(A cup B) = 3/4`. Then `P(A|B) P(A^(')|B) =`
View SolutionIf events A and B are independent, then `P(A cap B) =`
View SolutionTwo events E and F are independent. If P(E) = 0.3, `P(E cup F) = 0.5`, then P(E|F)-P(F|E) equals
View SolutionA bag contains 5 red and 3 blue balls. If 3 balls are drawn at random without replacement the probability of getting exactly one red ball is
View SolutionA bag containing 5 red and 3 blue balls. If 3 balls are drawn at random without replacement the probability that exactly two of the three balls were red, the first being red is
View SolutionAssume that in a family, each child is equally Iikely to be a boy or giris. A family with three children is choosen at random. The probability that the eldest child is a girl given that the fàmily has at least one girl is
View SolutionA die is thrown and a card is selected at random from a deck of 52 playing cards. The probability of getting an e: number on the die and a spade card is
View SolutionA box contains 3 orange balls, 3 green balls and 2 blue balls. Three balls are drawn at random from the box without replacement. The probability of drawing 2 green balls and one blue ball is
View SolutionA flashlight has 8 batteries out of which 3 are dead. If two batteries are selected without replacement and tested, the probability that both are dead is
View SolutionEight coins are tossed together. The probability of getting exactly 3 heads is
View SolutionTwo dice are thrown. If it is known that the sum of numbers on the dice was less than 6, the probability of getting a sum 3, is
View SolutionWhich one is not a requirement of a binomial distribution?
View SolutionTwo cards are drawn from a well shuffled deck of 52 playing cards with replacement. The probability, that both cards are queens is
View SolutionThe probability of guessing correctly at least 8 out of 10 answers on a true -false type examination is
View SolutionThe probability that a person is not swimmer is 0.3. The probability that out of 5 persons 4 are swimmer is
View SolutionThe probability distribution of a discrete random variable X is given below: The value of k is
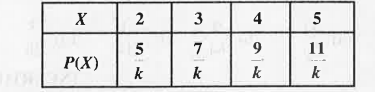
View SolutionFor the following probability distribution E(X) is equal to

View SolutionFor the following probability distribution `E(X^(2))` is equal to
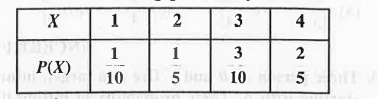
View SolutionSuppose a random variable X follows the binomial distribution with parameters n and p, where `0 lt p lt 1` .If P(x=r) / P(x=n-r) is independent of n and r, then p equals
View SolutionIn a college of 30 students fail in physics, 25 fail in mathematics and 10 fail in both. One student is chosen at random. The probability that she fails in physics, if she has failed in mathematics is
View SolutionA and B are two students. Their chances of solving a problem correctly are 1/3 and 1/4 respectively. If the probability of their making a common error is 1 20and they obtain the same answer, then the probability of their answer to be correct is
View SolutionA box has 100 pens of which 10 are defective. The probability that out of a sample of 5 pens drawn one by one with replacement and atmost one is defective is
View SolutionA problem in mathematics is given to three stdents A,B,C and their respective probability of solving the problem is `1/2,1/3 and 1/4` . Probability that the problem is solved is :
View SolutionIf A and B are two mutually exclusive events , then :
View SolutionA and B play a game where each is asked to select a number from 1 to 25 . If the two numbers match ,both of them win a prize . The probability that they will not win a prize in a straight trial is :
View SolutionThe probability of India winning a test match against Indies is `1/2` .Assuming indepeendence from match to match , the probability that in a 5 match series India's second win occurs at third test is :
View SolutionA fair die is tossed eight times . The probability that a thrid six is oberved on the 8th throw is :
View SolutionA dice is tossed 5 times . Getting an odd number is considered a success . Then the variance of distribution of number of successes is :
View SolutionEvents A, B, C are mutually exclusive events such that P(A) = (3x+1)/3, P(b) = (1-x)/4, P(C) = (1-2x). Then set of positive values of x are in the interval
View SolutionFive horses are in a rae . Mr . A selects two of the horses at random and bets on them . The probability that Mr. A selected the winning horse is :
View SolutionThe probabilit that A speaks truth is `4/5` , while the probability for B is `3/4`. The probability that they contradict each other when asked to speak on a facts is :
View SolutionA random variable X has the probability distribution: For the events E = {X is a prime number } and `F = {1 lt 4}`, the probability `P( E cup F) =`

View SolutionThe mean and variance of a binomial distribution are 4 and 2 respectively . Then the probability of 2 successes is :
View SolutionLet A and B two events such that `P( bar(A cup B)) = 1/6 , P(A capB) =1/4 and P(bar(A)) =1/4 , ` where `bar(A)` stands for complement of event A . Then events A and B are :
View SolutionThree houses are available in a localty . Three persons apply for the houses . Each applies for one house without consulting others . The probability that all three apply for the same house is :
View SolutionTwo numbers are chosen from [1,2,3,4,5,6] one after another without replacement . Find the probability that one of the smaller value of two is less than 4 :
View Solution`P(B) = 3/4 , P(bar(A) cap B cap bar(C )) = 1/3 . P (A cap B cap bar (C )) = 1/3 ` then `P (B cap C)` :
View SolutionIf three distinct numbers are chosen randomly from the first 100 natural numbers , then the probability that all three of them are divisible by 2 and 3 is :
View SolutionA fair die is thrown till we get . Then the probability of getting 1 in exactly even number of trials is :
View SolutionThe probability that A can solve a problem is 2/3 and B can solve is 3/4. If both of them attempt the problem, what is the probability that the problem get solved
View SolutionSix coins are tossed simultaneously. The probability of getting atleast 4 heads is
View SolutionThe probability that a candidate secures a seat in engg, through EAMCET is 1/10. 7 candidates are selected at random from a centre, The probability that exactly two will get seats is
View SolutionIf P(A) = 1/4, P(B) = 1/2, `P( A cup B) = 5/8` then `P(A cap B) =`
View SolutionThe probability that a isumtilci sefected at random from the set of nurnbeis 1,2,3 ….. 100 is a cube is
View SolutionThe probability of getting exactly 4 heads in 6 tosses of a coin is
View SolutionWhen two dice are thrown the probability of getting the sum, 10 or 11 is
View SolutionTwo unbiased six faced dice are thrown. The probability that the sum of the numbers on faces of them is a prime number greater than 5 is
View SolutionIf A and B are two events such that `P(A cup B) = 5/6`, `P(A cap B) = 1/3`, P(A) = 2/3, then A and B are
View SolutionThe probability of choosing at random a number that is divisible by 6 or 8 from among 1 to 90 is
View SolutionA and B are mutually exclusive events with P(A) = 1/2×P(B) and `A cup B = S`, the sample space. Then P(A) =
View SolutionA problem in mathematics is given to three stdents A,B,C and their respective probability of solving the problem is `1/2,1/3 and 1/4` . Probability that the problem is solved is :
View SolutionTwo dice are thrown at a time and the sum of the numbers on them is 6 . The probability of getting the number 4 on anyone of the dice is
View SolutionA random variable has the following distribution The value of of k and `P(X lt 3)` are equal to
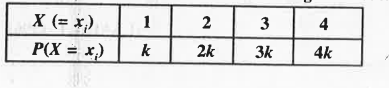
View SolutionA coin is tossed 3 times. The probability of getting head once and tail 2 times is
View SolutionA random variable X has the following distribution The mean and variance of X are

View SolutionThe probability of a man hitting the target is 1/4. If he fires 7 times, the probability of hitting the target at least twice is
View Solution
QUESTION BANK questions and complete solutions for chapter PROBABILITY of HIMALAYA MATHS (KANNADA ENGLISH) of Class 12