Complete Solutions to Questions (Section A) of chapter SAMPLE PAPER 01 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | SAMPLE PAPER 01 |
| OSWAL GURUKUL | Questions (Section A) |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
Check whether the relation R defined in the set A of all the newspapers in an auditorium of a library given by R= {(a, b): a and I have the equal number of pages} iS :
View SolutionGiven that `f : x rarr 3x - 5` and `g : x rarr x^(3)` for all `x in R`. The value of f[g(x) + 5] is:
View SolutionFind the value of sin `(cos^(-1)""(3)/(5))`
View SolutionFind the domain of the function defined by `f(x) = sin^(-1)sqrt(x-1)`
View SolutionFind the minimum value of n for which `cos^(-1)((n)/(2)) gt (pi)/(6), n in N` is valid.
View SolutionLet A be the set of all human beings in a city at a particular time. Then the relation Rin A is defined by R= {(x, y):x is father of y) is:
View SolutionIf `A_(ij)` be the co-factors for the determinant `|(1,0,-2),(3,-1,2),(4,5,6)|`, then evaluate `A_(13) + A_(21)`.
View SolutionA matrix of order `2 xx 3` is equal to the another matrix of order `3 xx 2`. This statement is:,
View SolutionIf `A = [[-1,4],[2,1]]`, find `A^(2)`.
View SolutionIf A be any square matrix, then A+ A' iş:
View SolutionIf A and B be two non-singular matrices of the same type, then
View SolutionEvaluate : `|(6,2,6),(-3,-1,-3),(1,4,12)|`
View SolutionIf `y = t^(3) + 3t^(2)` and `t = 4x - 5`, find `(dy)/(dx)`
View SolutionFind the value of `lim_(x rarr 0)""(1- cos x)/(x^(2))`.
View SolutionDifferentiate `y = sin^(2)x` with respect to x.
View SolutionWhat will be the value of `(dy)/(dx)` If `y = cos^(-1)(sin x)` ?
View SolutionThe value of `lim_(x rarr 0)""(sin x)/(x)` is equal to : Find the slope of the tangent to the curve `y = 3x^(2) - 2x - 1` at x = 2.
View SolutionFind the slope of the tangent to the curve `y = 3x^(2) - 2x - 1` at x = 2.
View SolutionThe second derivative of `y = 4x^(3) - 5x + 7` is :
View SolutionIf `tan^(-1)a + tan^(-1)b + tan^(-1)c = pi`, the value of a + b + c is :
View SolutionAnsh bought 5 pens, 3 pencils and 1 geometry boxes. From the same shop Rajat bought 2 pens 1 pencil and 3 geometry boxes. Yuvan bought 1 pen, 2 pencils and 4 geometry boxes. Ansh, Rajat and Yuvan paid Rs. 15, Rs.19 and Rs. 25 respectively for their items.
Using the concept of matrices and determinants to answer the following questions by choosing the correct option :
If x, y and z be the cost of pen, pencil and geometry box, which equation (s) is/are true ?
View SolutionAnsh bought 5 pens, 3 pencils and 1 geometry boxes. From the same shop Rajat bought 2 pens 1 pencil and 3 geometry boxes. Yuvan bought 1 pen, 2 pencils and 4 geometry boxes. Ansh, Rajat and Yuvan paid Rs. 15, Rs.19 and Rs. 25 respectively for their items.
Using the concept of matrices and determinants to answer the following questions by choosing the correct option :
If `A = |(1,2,4),(2,1,3),(5,3,1)|`, the value of |A| is :
View SolutionAnsh bought 5 pens, 3 pencils and 1 geometry boxes. From the same shop Rajat bought 2 pens 1 pencil and 3 geometry boxes. Yuvan bought 1 pen, 2 pencils and 4 geometry boxes. Ansh, Rajat and Yuvan paid Rs. 15, Rs.19 and Rs. 25 respectively for their items.
Using the concept of matrices and determinants to answer the following questions by choosing the correct option :
If `A = |(5,3,1),(2,1,4),(1,2,4)|` and adj `A = |(-2, -10, 8),(-5, y, -13),(x, -7, -1)|`, find the values of x and y.
View SolutionAnsh bought 5 pens, 3 pencils and 1 geometry boxes. From the same shop Rajat bought 2 pens 1 pencil and 3 geometry boxes. Yuvan bought 1 pen, 2 pencils and 4 geometry boxes. Ansh, Rajat and Yuvan paid Rs. 15, Rs.19 and Rs. 25 respectively for their items.
Using the concept of matrices and determinants to answer the following questions by choosing the correct option :
Find the cost of one geometry box.
View SolutionAn iron bridge in form of a trapezium is placed to cross over a railway tack 10m wide.

Find the value of DP if AP = QB = x m and AD = BC = 10 m.
View SolutionAn iron bridge in form of a trapezium is placed to cross over a railway tack 10m wide.
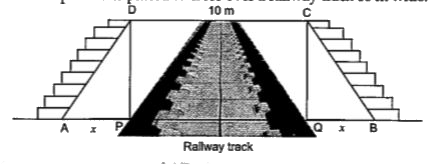
If S is the area of trapezium, find the value of S.
View SolutionAn iron bridge in form of a trapezium is placed to cross over a railway tack 10m wide.
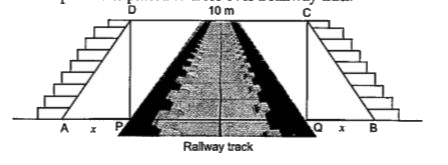
Find the value of x at which first derivative of S = 0.
View SolutionAn iron bridge in form of a trapezium is placed to cross over a railway tack 10m wide.
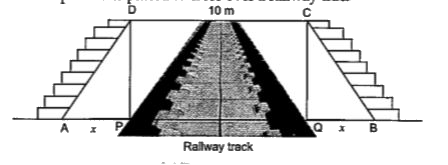
For which possible value x, S(x) has maximum value.
View SolutionFor the function `f(x) = {{:(|x-3|,"," x ge 1),((1)/(4)(x^(2) - 6x + 13),"," x lt 1):}`
Answer the following questions :
R.H.D. of f(x) at x = 1 is :
View SolutionFor the function `f(x) = {{:(|x-3|,"," x ge 1),((1)/(4)(x^(2) - 6x + 13),"," x lt 1):}`
Answer the following questions :
L.H.D. of f(x) at x = 1 is :
View SolutionFor the function `f(x) = {{:(|x-3|,"," x ge 1),((1)/(4)(x^(2) - 6x + 13),"," x lt 1):}`
Answer the following questions :
f(x) is not differentiable at :
View SolutionFor the function `f(x) = {{:(|x-3|,"," x ge 1),((1)/(4)(x^(2) - 6x + 13),"," x lt 1):}`
Answer the following questions :
The value of f'(-1) is :
View Solution
Questions (Section A) questions and complete solutions for chapter SAMPLE PAPER 01 of ARYA MATHS (ENGLISH) of Class 12