Complete Solutions to SECTION - A of chapter MODEL TEST PAPER - 10 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MODEL TEST PAPER - 10 |
| VIVA PUBLICATION | SECTION - A |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
Let `f:R to R` defined by `f(x)=x^(2)+1, forall x in R`. Choose the correct answer
View SolutionFor a `2^(nd)` order determinant `abs(A)=abs(a_(ij))`, find `a_(12)A_(11)+a_(22)A_(21)`
View SolutionIf A and B are symmetric matrices of same order, then AB - BA is a
View SolutionOn which of the following intervals is the function f given by
`f(x)=x^(100)+sinx-1` strictly decreasing?
View SolutionThe functions `g(x)=x-[x]` is discontinuous at x =
View SolutionTwo events A and B will be independent, if
View SolutionThe circle shown in the figure has radius a ft. As the point P moves to the right at the rate of 7 ft/sec, how fast does the arc BQ increase?
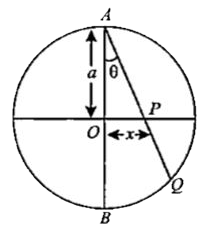
View SolutionLet `A=[{:(2, -1, 3), (4, 0, 2), (-3, 2, 6):}]`, find det (adj A).
View Solutionif `abs({:(sinalpha, cosbeta), (cosalpha, sinbeta):})=1/2`, where `alpha, beta` are acute angles, then find the value of `alpha+beta`. a) `pi/3` b) `(2pi)/3``c) `pi/2` d) `pi/4`
View SolutionR be a relation on Q (set of all rational numbers) defined by `R={(x, y):1+xy gt 0}`. Then the relation R is
View SolutionThe probabilities that the events A and B occur are 0.3 and 0.4 respectively. The probability that both A and B occur simultaneously is 0.15. What is the probability that neither A nor B occurs?
View SolutionIf P(not B) = 0.65, `P(A cup B)=0.85` and A and B are independent events, then find P(A).
View SolutionFind the differential equation of the family of all circles which pass through the origin and whose centre lie on y-axis.
View SolutionExpress in simplest form: `cos^(-1)(3/5cosx+4/5sinx)`
View SolutionConsider the binary operations `""^('ast')` and 'o' on R defined as `a^(ast)b=abs(a-b) and aob=a`, for all `a, b in R`. Show that `a^(ast)(boc)=(a^(ast)b)oc` for all a, b, c `in` R.
View SolutionIf `y=sqrt(x+sqrt(x+sqrt(x+.........+infty)))," find "(dy)/(dx)`.
View SolutionEvaluate: `lim_(x to 0)(cotx)^(sin2x)`
View SolutionShow that: `sin^(-1)(3/5)-sin^(-1)(8/17)=cos^(-1)(84/85)`
View SolutionFind the interval in which the function `f(x)=x/2+2/x, x < 0` is decreasing.
View Solution`inttan^(-1)xdx=xtan^(-1)x+f(x)+C, " find "f(x)`.
View SolutionEvaluate: `int(sin(a-x))/(sinx)dx`
View SolutionSolve the `(xdy-ydx)ysin(y/x)=(ydx+xdy)xcos(y/x)`
View SolutionProve that the function `f:N to N`, defined by `f(x)=x^(2)+x+1` is one-one but not onto.
View SolutionA pair of dice is thrown 7 times. If getting a total of 7 is considered a success, what is the probability of atmost 6 success?
View SolutionEvaluate: `int(xsin^(-1)x)/sqrt(1-x^(2))dx`
View SolutionEvaluate the integral as limit of sum: `int_(0)^(pi)sinxdx`
View SolutionLet `f(x)={{:((log(1+ax)-log(1-bx))/x, x ne 0), (k,x=0):}`.
Find 'k' so that f(x) is continuous at x = 0.
View SolutionIf `x=2(theta-sintheta) and y=2(1+costheta), " find "(d^(2)y)/(dx^(2))" at "theta=pi/3`.
View SolutionUsing properties of determinant, prove that `|{:(a^(2)+2a, 2a+1, 1), (2a+1, a+2, 1), (3, 3, 1):}|=(a-1)^(3)`
View SolutionIf `A=[{:(9, 7, 3), (5, -1, 4), (6, 8, 2):}]" find "A^(-1)` and hence solve the system of equations:
`9x+7y+3z=6, 5x-y+4z=1, 6x+8y+2z=4`.
View SolutionFind the maximum volume of a cylinder, generated by rotating a rectangle of perimeter 48 cm about one of its sides.
View SolutionA point P is given on the circumference of a circle of radius r. Chord QR is parallel to the tangent at P. Determine the maximum possible area of the triangle PQR.
View SolutionEvaluate: `int cos^(-1)sqrt(x)dx`
View SolutionIn an entrance examination, a candidate is to answer a multiple choice question which has four alternative solutions. The candidate either guesses the answer or he knows the answer. The probability that he knows the answer is 0.6. The examiner has found that the candidate has answered the question correctly. Find the probability that the candidate knew the answer, given that he answered it correctly.
View Solution
SECTION - A questions and complete solutions for chapter MODEL TEST PAPER - 10 of ARYA MATHS (ENGLISH) of Class 12