Complete Solutions to SECTION-A of chapter MATHEMATICS-2012 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MATHEMATICS-2012 |
| GURUKUL PUBLICATION | SECTION-A |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
Solve for y if `y^(2) + 2(2 + 3y) = 1(-14 - 5y)`.
View SolutionFind the value of:`3sin(pi/6) sec(pi/3) 4sin((5pi)/6) cot(pi/4)`
View SolutionFind the equation of the hyperbola whose transverse and conjugate axes are the x and y axes respectively, given that the length of conjugate axis is 5 and distance between the foci is 13.
View SolutionFrom the equation of the two lines, `4x + 3y +7=0` and `3x + 4y +8=0`, Find the mean of `x and y` .
View SolutionEvaluate: `int e^(x) (tan x + log sec x) dx`.
View SolutionFind: `d/dx` of `( Log tan x)`
View SolutionFind the locus of the complex number, `Z = x + iy`
given, `|(x+iy-2i)/(x+iy+2i)|= sqrt(2)`
View SolutionEvaluate: `int_(1)^(2) (sqrt(x))/(sqrt(3-x) + sqrt(x)) dx`.
View SolutionThree persons A, B and C shoot to hit a target. If in trials, A hits the target 4 times in 5 shots, B hits 3 times in 4 shots and C hits 2 times in 3 trials. Find the probability that: Exactly two persons hit the target.
View SolutionSolve the differential equation ,
`(xy^(2) + x) dx + (x^(2)y +y)dy=0`
View SolutionUsing properties of determinants, prove that:
`|{:(a, a +b, a+b+c),(2a, 3a + 2b, 4a + 3b + 2c),(3a, 6a+3b, 10a + 6b + 3c):}| = a^(3)`
View SolutionFind the product of matrices A and B, where `A= [(-5,1,3),(7,1,-5),(1,-1,1)] and B= [(1,1,2),(3,2,1),(2,1,3)]`. Hence, solve the following equations by matrix method:
`x+y+2z=1, 3x+ 2y + z= 7, 2x+ y + 3z= 2`
View SolutionProve that: `"cos"^(-1)63/65+2"tan"^(-1)1/5="sin"^(-1)3/5`
View SolutionVerify Rolle theorem for the function `f(x)=log{(x^2+a b)/(x(a+b))}on[a , b],` where `0
View SolutionFind the equation of the ellipse with its centre at (4, -1), focus at (1, -1), and passing through (8, 0).
View SolutionIf ` e^(y) (x+1) =1 ` show that ` (d^(2) y)/( dx^(2)) = ((dy)/(dx))^(2) `
View SolutionA printed page is to have total area of 80 sq. cm with a margin of 2 cm at the top and on each side and a margin of 2.5cm at the bottom. What should be the dimensions of the page so that the printed area will be maximum?
View SolutionEvaluate: `int1/(x\ {6\ (logx)^2+7logx+2})\ dx`
View SolutionFind the area of the region bounded by the curves `x=4y-y^(2)` and the Y-axis.
View SolutionTen candidates received percentage marks in two subjects as follows:
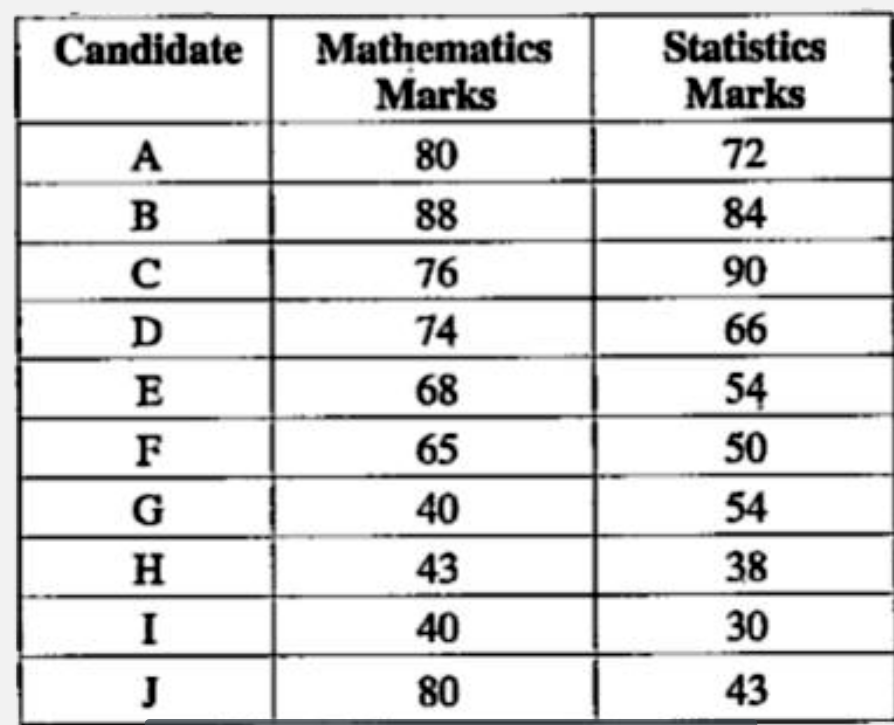
Calculate Spearman's rank correlation coefficient and interpret your result.
View SolutionThe following results were obtained with respect to two variable x and y:
`sumx = 30, sum y = 42, sumxy = 199, sumx^(2) = 184, sumy^(2) = 318, n=6`.
Find the following:
(i) The regression coefficients.
(ii) Correlation coefficient between x and y.
(iii) Regression equation of y on x.
(iv) The likely value of y when x = 10.
View SolutionA bag contains 8 red and 5 white balls. Two successive draws of 3 balls are made at random from the bag without replacements. Find the probability that the first draw yields 3 white balls and the second draw 3 red balls.
View SolutionA box contains 30 bolts and 40 nuts. Half of the bolts and half of the nuts are rusted. If two items are drawn at random from the box, what is the probability that either both are rusted or both are bolts ?
View SolutionUsing De Moivre 's theorem prove that :
`((1+cos theta +i sin theta)/(1+cos theta - i sin theta))^n= cos n theta + i sin n theta`, where `i = sqrt(-1)`
View SolutionSolve the differential equation :
`(dy)/(dx) -3ycotx = sin 2x`, given y=2, when `x=pi/2`
View Solution
SECTION-A questions and complete solutions for chapter MATHEMATICS-2012 of ARYA MATHS (ENGLISH) of Class 12