Complete Solutions to Section-A of chapter MATHEMATICS - 2014 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MATHEMATICS - 2014 |
| GURUKUL PUBLICATION | Section-A |
| Number Of Questions | 26 |
| Academic Year | 2023-24 |
If `A=[{:(3,1),(7,5):}]` find the values of x and y such that `A^(2)+xI_(2)=yA`
View SolutionFind the eccentricity and the coordinate of foci of the hyperbola `25 x ^(2) - 9y ^(2) = 225.`
View SolutionEvaluate : `tan[2tan^(-1)(1/2)-cot^(-1)3]`
View SolutionUsing L' Hospital's Rule evaluate :
`Lim_(x to o)(1+sinx)^(cotx)`
View SolutionEvaluate : `inte^(x).((2+sin2x))/(cos^(2)x)dx`
View SolutionUsing properties of definite integrals, evaluate
`int_(0)^(pi//2)(sqrt(sinx))/(sqrt(sinx)+sqrt(cosx))dx`
View SolutionFor the given lines of regression, 3x – 2y = 5 and x - 4y - 7, find
regression coefficients byx and bxy
View SolutionExpress the comple number `((1+sqrt(3)i)^(2))/(sqrt(3)-i)` in the form of `a+ib` . Hence find the modulus and argument of the complex number.
View SolutionA bag contains 20 balls numbered from 1 to 20 . One ball is drawn at random from the bag. What is the probability that the ball drawn is marked with a number which is multiple of 3 or 4 ?
View SolutionSolve the differential equation
`(x+1)dy-2xydx=0`
View SolutionUsing properties of determinants, prove that :
`|{:(a^(2)+1,ab,ac),(ba,b^(2)+1,bc),(ca,cb,c^(2)+1):}|=a^(2)+b^(2)+c^(2)+1`
View SolutionUsing matrix method, solve the following system of equation
`x-2y=10,2x+y+3z=8` and `-2y+z=7`
View SolutionIf `cos^(-1)x+cos^(-1)y+cos^(-1)z=pi`, prove that `x^(2)+y^(2)+z^(2)+2xyz=1`
View SolutionP,Q and R represent switches in on position and P',Q' and R' represent switches in off position. Construct a switching circuit representing the polynomial `PR+Q(Q'+R)(P-: QR)` . Using Boolean Algebra, simplify the polynomial expression and construct the simplified circuit
View SolutionVerify Rolle's theorem for the function `f(x)=e^(x)(sinx-cosx)` on `[(pi)/(4),(5pi)/(4)]`
View SolutionFind the distance between points `A(4,6)` and `B(4,-2)` .
View SolutionIf `y=(xsin^(-1)x)/(sqrt(1-x^2)),` prove that `(1-x^2)(dy)/(dx)=x+y/xdot`
View SolutionA wire of length 36m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces, so that the combined area of the square and the circle is minimum?
View SolutionEvaluate `int(x+sinx)/(1+cosx)dx`
View SolutionSketch the graphs of the curves `y^(2)=x` and `y^(2)=4-3x` and the area enclosed between them
View SolutionA psychologist selected a random sample of 22 students. He grouped them in 11 pairs so that the students in each pair have nearly equal scores in an intelligence test. In each pair one student was taught by method A and the other by method B and examined after the course. The marks obtained by them after the course are as follows
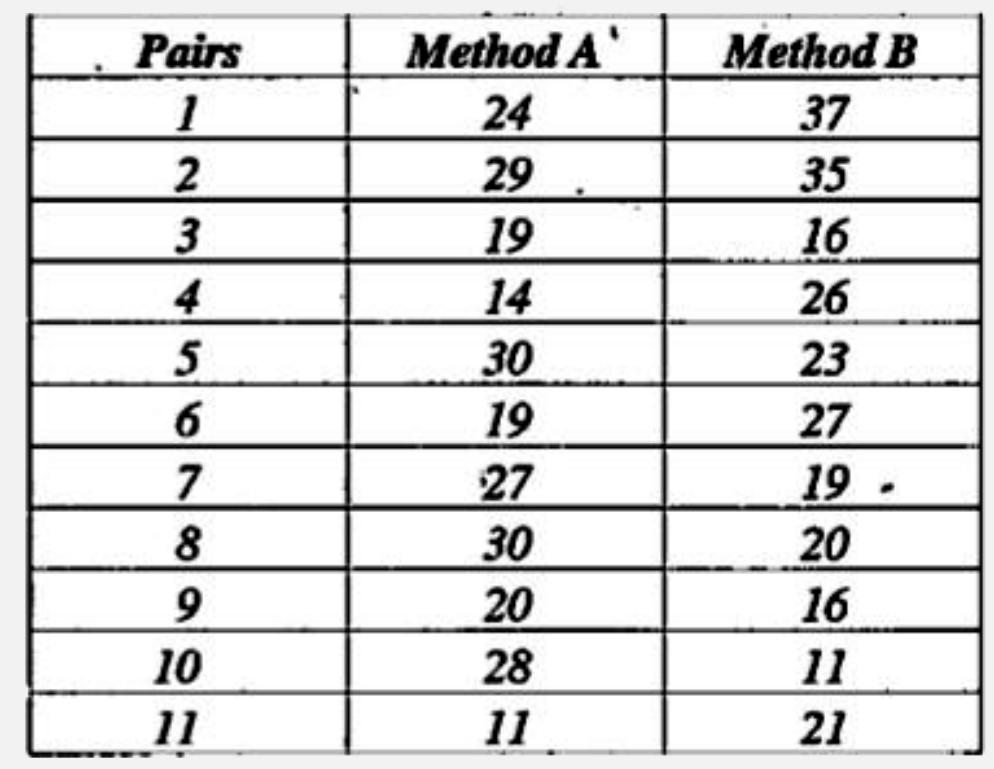
Calculate Spearman's Rank correlation
View SolutionThe coefficient of correlation between the values denoted by X and Y is `0.5`. The mean of X is 3 and that of Y is 5. Their standard deviations are 5 and 4 respectively. Find
(i) the two lines of regression.
(ii) the expected value of Y, when X is given 14
(iii) the expected value of when Y is given 9
View SolutionIn a college, `70%` students pass in Physics, `75%` pass in Mathematics and `10%` students fail in both. One student is chosen at random. What is the probability that
(i) He passes in Physics and Mathematics
(ii) He passes in Mathematics given that he passes in Physics
(iii) He passes in Physics given that he passes in Mathematics.
View SolutionA bag contains 5 white and 4 black balls and another bag contains 7 white and 9 black balls. A ball is drawn from the first bag and two balls drawn from the second bag. What is the probability of drawing one white and two black balls ?
View SolutionUsing De Moivre's theorem, find the least positive integer n such that `((2i)/(1+i))^(n)` is a positive integer.
View SolutionSolve the following differential equation
`(3xy+y^(2))dx+(x^(2)+xy)dy=0`
View Solution
Section-A questions and complete solutions for chapter MATHEMATICS - 2014 of ARYA MATHS (ENGLISH) of Class 12