Complete Solutions to SECTIONS-C of chapter MODEL TEST PAPER 15 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MODEL TEST PAPER 15 |
| VIVA PUBLICATION | SECTIONS-C |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
The marginal cost function of manufacturing x units of a product is given by `MC = 3x^(2) - 10x +3`, then the total cost for producing one unit of the product is Rs. 7. Find the total cost function.
View SolutionThe equations of two regression lines are : `13x-10y+11=0` and `2x-y-1=0`. Find the ratio between mean of y serise and mean of x series.
View SolutionA manufacturer can sell x items of a commodity at price Rs (330-x) each and the cost of producing x items is Rs `(x^(2)+10x+12)`. Find MAR.
View SolutionIf the regression coefficients be given by `b_(yx)=(2)/(9)` and `b_(xy)=2` and `theta` be angle between the regression lines find the value of `theta.
View SolutionA text-book publisher finds that the production costs directly attribute to each book are of Rs 20 and the fixed costs are Rs 10,000. If each book can be sold for Rs 30, determine the break-even point.
View SolutionThe marginal revenue function of a commodity is `MR = 9 + 2x - 6x^(2)`, find the total revenue function.
View SolutionA radio manufacturer finds that he can sell x radios per week at Rs p each where `p=2(100-(x)/(4))`. His average cost of production of x radios per week is Rs `(120x+(x^2)/(2))`. Show that this profit is maximum when the production is 40 radios per week.
View SolutionFrom the following data, find
Regression equations.
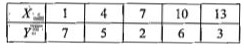
View SolutionAlso find the value of y when x=11 and value of x when y=10.
View Solution(Manufacturing problem) A manufacturing company makes two models A and B of a product. Each piece of Model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of Model B requires 12 labour hours for fabricating a
View SolutionFind graphically, the maximum value of `Z=(3)/(4)x+(1)/(2)y`
Subject to the constraints: `2x+yle180,xge20,2x+3yge120,x,yge0`
View Solution
SECTIONS-C questions and complete solutions for chapter MODEL TEST PAPER 15 of ARYA MATHS (ENGLISH) of Class 12