Complete Solutions to SECTION-A of chapter MATHEMATICS-2016 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MATHEMATICS-2016 |
| GURUKUL PUBLICATION | SECTION-A |
| Number Of Questions | 26 |
| Academic Year | 2023-24 |
Solve the matrix equation `[[5 ,4] ,[1 ,1]]X=[[1,-2],[ 1 ,3]]` , where `X` is a `2xx2` matrix.
View SolutionSolve for x, if : `tan (cos^(-1)x)=(2)/(sqrt(5))`
View SolutionThe line `2x-3y=9` touches the conics `y^(2)=-8x`. find the point of contact.
View SolutionUsing L' Hospital's rule, evaluate:
`lim_(x to 0) ((1)/(x^(2))-(cotx)/(x))`
View SolutionUsing L' Hospital's rule evaluate:
`lim_(x to 0) (e^x−1)/x`
View SolutionUsing properties of definite integrals, evaluate:
`int_(0)^(pi//2) (sin x - cos x)/(1+sin x cos x) dx`
View SolutionThe two lines of of regressions are `x+2y-5=0` and `2x+3y-8=0` and the variance of x is 12. Find the variance of y and the coefficient of correlation.
View SolutionExpress `(2+i)/((1+i)(1-2i))` in the form of `a+ib`. Find its modulus .
View SolutionA pair of dice is thrown. What is the probability of getting an even number on the first die or a total of 8?
View SolutionSolve the differential equation:
`x (dy)/(dx)+y=3x^(2)-2`
View SolutionUsing properties of determinants, show that `|(b+c,a,a),(b,c+a,b),(c,c,a+b)|=4abc`
View SolutionSolve the following system of linear equations using matrix method : `3x + y + z = 1, 2x + 2z =0, 5x + y + 2z = 0`.
View SolutionIf `sin^(-1)x+tan^(-1)x=(pi)/(2)`, prove that :
`2x^(2)+1=sqrt(5)`
View SolutionWrite the Boolean function coresponding to the switching circuit given below:

A, B and C represent switches in 'on' position and A', B' and C' represent them in 'off' position. Using Boolean algebra, simplify the function and construct an equivalent switching circuit.
View SolutionVerify the conditions of Rolle's theorem for the following function:
`f(x)=log (x^(2)+2)-log 3` on [ -1, 1]
Find a point in the interval, where the tangent to the curve is parallel to X-axis.
View SolutionFind the equation of the standard ellipse, taking its axes as the coordinate axes, whose minor axis is equal to the distance between the foci and whose length of latus rectum is 10. Also, find its eccentricity.
View SolutionIf `logy=tan^(-1)x`, prove that : `(1+x^(2)) (d^(2)y)/(dx^(2))+(2x-1)(dy)/(dx)=0`
View SolutionA rectangle is inscribed in a semi-circle of radius `r` with one of its sides on diameter of semi-circle. Find the dimensions of the rectangle so that its area is maximum. Find also the area.
View SolutionEvaluate : `int (sin x+ cos x)/(sqrt(9+16sin2x))dx`
View SolutionFind the area bounded by the curves `y=6x -x^(2) and y= x^(2)-2x`
View SolutionCalculate Karl Pearson's coefficient of correlation between x and y for the following data and interpret the result:
(1, 6), (2, 5), (3, 7), (4, 9), (5, 8), (6, 10), (7, 11), (8, 13), (9, 12).
View SolutionThe marks obtained by 10 candidates in English and Mathematics are given below:
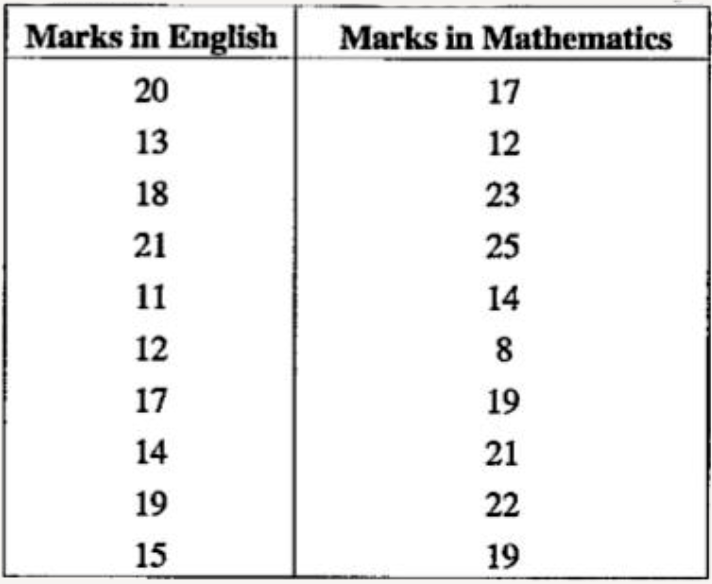
Estimate the probable score for Mathematics if the marks obtained in English are 24.
View SolutionA committee of 4 persons has to be chosen from 8 boys and 6 girls, consisting of at least one girl. Find the probability that the committee consists of more girls than boys.
View SolutionAn urn contains 10 white and 3 black balls. Another urn contains 3 white and 5 black balls. Two are drawn from first and put into the second urn and then a ball is drawn from the latter. Find the probability that it is a white ball.
View SolutionFind the locus of a complex number, `z=x +iy`, satisfying the relation `|(z-3i)/(z+3i)| le sqrt(2)`. Illustrate the locus of z in the Argand plane.
View SolutionSolve the following differential equation:
`x^(2)dy=(xy+y^(2))dx=0`, when `x=1 and y=1`
View Solution
SECTION-A questions and complete solutions for chapter MATHEMATICS-2016 of ARYA MATHS (ENGLISH) of Class 12