Complete Solutions to SECTION C of chapter MATHEMATICS-2020 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MATHEMATICS-2020 |
| GURUKUL PUBLICATION | SECTION C |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
The selling price of a commodity is fixed at Rs 60 and its cost function is `C(x)=35x+250`
(i) Determine the profit function.
(ii) Find the break even points.
View SolutionThe revenus function is given by `R (x) = 100 x -x ^(2) -x ^(3) .` Find
Marginal revenue function.
View SolutionFor the lines of regression `4x-2y=4and2x-3y+6=0`, find the mean of 'x' and the mean of 'y'.
View SolutionThe correlation coefficient between x and y is 0.6. If the variance of x is 225, th variance of y is 400, mean of x is 10 and mean of y is 20, find the equation of two regression lines.
View SolutionFind the regression coefficients `b_(yx) and b_(xy)` and the two lines of regression for the following data:
`{:(x,2,6,4,7,5),(y,8,8,5,6,2):}`
View SolutionThe marginal cost of the production of the commodity is `30+2x`, it is known that fixed costs are Rs 200, find
(i) The total cost.
(ii) The cost of increasing output from 100 to 200 units.
View SolutionThe total cost function of a firm is given by `C(x)=1/(3)x^(3)-5x^(2)+30x-15` where the selling price per unit is given as Rs 6. Find for what value of x will the profit be maximum.
View SolutionA company uses three machines to manufacture two types of shirts, half sleeves and full sleeves. The number of hours required per week on machine `M_(1),M_(2)andM_(3)` for one shirt of each type is given in the following table :
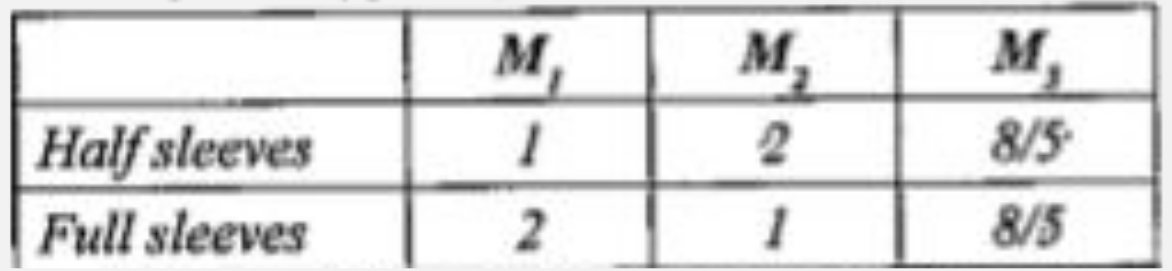
None of the machines can be in operation for more than 40 hours per week. The profit on each half sleeve shirt is Rs 1 and the profit on each full sleeve shirt is Rs 1.50. How many of each type of shirts should be made per week to maximize the company's profit ?
View Solution
SECTION C questions and complete solutions for chapter MATHEMATICS-2020 of ARYA MATHS (ENGLISH) of Class 12