Complete Solutions to Mathematics (Section B) of chapter JEE MAINS 2021 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | JEE MAINS 2021 |
| JEE MAINS PREVIOUS YEAR | Mathematics (Section B) |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
Let the equation `x^(2)+y^(2)+px+(1-p)y=0` represent circles of varying radius `r in (0,5]`. Then the number of elements in the set `S={q : q =p^(2)` and q is an integer } is __________.
View SolutionIf `y^(1//4)+y^(-1//4)=2x`, and `(x^(2)-1)(d^(2)y)/(dx^(2))+alphax(dy)/(dx)+betay=0`, then `|alpha-beta|` is equal to ___________
View SolutionLet n be an odd natural number such that the variance of 1,2,3,4,...., n is 14. Then n is equal to ___________.
View SolutionIf the system of linear equations
`{:(2x+y-z=3),(x-y-z=alpha),(3x+33y-betaz=3):}` has infinitely many solution, then `alpha+beta-alphabeta` is equal to ______.
View SolutionIf `A={x in R : |x-2| gt 1}`, `B={x in R : sqrt(x^(2)-3) gt 1 }`, `C={x in R : |x-4| ge 2}` and Z is the set of all integers, then the number of subsets of the set `(AnnBnnC)^(c )nnZ` is ___________.
View SolutionIf the minimum area of the triangle formed by a tangent to the ellipse `(x^(2))/(b^(2))+(y^(2))/(4a^(2))=1` and the co-ordinate axis is kab, then k is equal to ____________.
View SolutionA number is called a palindrome if it reads the same backward as well as forward. For example 285582 is a six digit palindrome. The number of six digit palindromes, which are divisible by 55 is________.
View SolutionLet `veca=hati+5 hat j+alpha hat k`, `vecb=hati+3hatj+betahatk` and `vec c=-hati+2hatj-3hatk` be three vectors such that, `|vecbxxvec c|=5sqrt(3)` and `veca` is perpendicular to `vecb`. Then the greatest amongst the values of `|veca|^(2)` is ____________.
View SolutionIf `int(dx)/((x^(2)+x+1)^(2))=atan^(-1)((2x+1)/(sqrt(3)))+b((2x+1)/(x^(2)+x+1))+C`, `x gt 0` where C is the constant of integration, then the value of `9(sqrt(3)a+b)` is equal to __________.
View SolutionThe number of distinct real roots of the equation `3x^(4)+4x^(3)-12x^(2)+4=0` is ___________.
View SolutionThe least positive integer n such that `((2i)^n)/((1-i)^(n-2)),i=sqrt(-1)`, is a positive integer,is ______
View SolutionLet the mean and variance of four numbers 3, 7, x and y `(x gt y)` be 5 and 10 respectively. Then the mean of four numbers 3 + 2x, 7 + 2y, x + y and x - y is ___ _
View SolutionLet `a_1, a_2, ... , a_(10)` be an AP with common difference - 3 and `b_1, b_2`, ... , `b_(10)` be a GP with 10 common ratio 2. Let `c_k= a_k + b_k, k = 1, 2, ... , 10`. If `c_2 = 12` and `c_3= 13`, then `sum_(k=1)^(10)` ck is equal to _____
View SolutionLet `lamdane 0` be in R. If `alpha` and `beta` are the roots of the equation `x^(2) - x + 2lamda = 0`, and `alpha` and `gamma` are the roots of the equation `3x^2 - 10x + 27lamda = 0`, then `(betagamma)/lamda` is equal to __________
View SolutionLet A be a `3xx3` real matrix. If det(2 Adj(2 Adj(Adj (2A)))) = `2^(41)`, then the value of det `(A^2)` equals _______
View SolutionLet Q be the foot of the perpendicular from the point P(7, - 2, 13) on the plane containing the lines `(x+1)/6=(y-1)/7=(z-3)/8` and `(x-1)/3=(y-2)/5=(z-3)/7`.
Then `(PQ)^2`, is equal to ____
View SolutionThe sum of all 3-digit numbers less than or equal to 500, that are formed without using the digit "1" and they all are multiple of 11, is ___________.
View SolutionLet `({:(n),(k):})` denote `""^(n)C_k` and

If `A_k=sum_(i=0)^9({:(9),(i):})[{:(" 12"),(12-k+i):}]+sum_(i=0)^8({:(8),(i):})[{:(" 13"),(13-k+i):}]`and `A_4 -A_3= 190p` ,then p is equal to
View SolutionIf the projection of the vector `hati + 2 hatj + hatk` on the sum of the two vectors `2hati + 4hatj - 5hatk` and `-lamdahati+2hatj+ 3hatk` is 1, then `lamda` is equal to _______
View SolutionLet a and b respectively be the points of local maximum and local minimum of the function
`f (x) = 2x^3 - 3x^2 - 12x.`
If A is the total area of the region bounded by y = f (x), the x-axis and the lines x = a and x = b, then 4 A is equal to __________.
View SolutionIf `int(2e^(x) +3e^(-x))/(4e^(x)+7e^(-x))dx=(1)/(14)(ux+v log_(e ) (4e^(x)+7e^(-x)))+C`, where C is a constant of integration, then ` u+v ` is equal to ________.
View SolutionLet S={1, 2,3, 4,5, 6, 9}. Then the number of elements in the set `T={A subeS:A ne phi` and the sum of all the elements of A is not a multiple of 3} is ____________.
View SolutionThe probability distribution of random variable X is given by :

Let `p=P(1 lt X lt 4"|"X lt 3)`. If `5p=lambda K`, then `lambda` is equal to _________.
View SolutionLet S be the sum of all solutions (in radians) of the equation `sin^(4) theta +cos^(4) theta - sin theta cos theta =0` in `[0, 4pi]`. Then `(8S)/(pi)` is equal to ________.
View Solution`3 xx 7^(22) + 2 xx 10^(22) -44` when divided by 18 leaves the remainder ________.
View SolutionTwo circles each of radius 5 units touch each other at the point (1, 2). If the equation of their common tangent is `4x+3y=10`, and `C_(1)(alpha, beta) and C_(2)(gamma, delta), C_(1) ne C_(2)` are their centres, then `|(alpha+beta) (gamma+delta)|` is equal to _______.
View SolutionAn online exam is attempted by 50 candidates out of which 20 are boys. The average marks obtained by boys is 12 with a variance 2. The variance of marks obtained by 30 girls is also 2. The average marks of all 50 candidates is 15. If `mu` is the average marks of girls and `sigma^(2)` is the variance of marks of 50 candidates, then `mu+sigma^(2)` is equal to __________.
View SolutionLet `A(sec theta , 2 tan theta) and B(sec phi , 2 tan phi)`, where `theta+phi=pi//2` be two points on the hyperbola `2x^(2)-y^(2)=2`. If `(alpha, beta)` is the point of the intersection of the normals to the hyperbola at A and B, then `(2beta)^(2)` is equal to _________.
View SolutionLet S be the mirror image of the point Q(1, 3, 4) with respect to the plane `2x-y+z+3=0` and let R `(3,5, gamma)` be a point of this plane. Then the square of the length of the line segment SR is __________.
View SolutionLet `z_(1)` and `z_(2)` be two complex numbers such that arg `(z_(1)-z_(2))=(pi)/(4) and z_(1), z_(2)` satisfy the equation `|z-3|=Re(z)`. Then the imaginary part of `z_(1)+z_(2)` is equal to ________.
View SolutionThe mean of 10 number
`7xx8,10xx10,13xx12,16xx14…` is ______
View SolutionLet [t] denote the greatest integer `le` t. Then the value of 8 `underset(-1/2)overset(1)int [2x]+|x| dx` is ____________
View SolutionIf yR' is the least value of 'a' such that the function f(x) = `x^(2) + ax +1` is increasing on [1, 2] and 'S' is the greatest value of ' a' such that the function f(x) = `x^(2) + ax +1` is decreasing on [1, 2], then the value of |R — S| is_____________
View SolutionIf `(3^(6))/(4^(4))` k is the term, independent of x in the binomial expansion of `((x)/(4)-(12)/(x^(2)))^(12)` then k is equal to ____________
View SolutionAn instrument consists of two units. Each unit must function for the instrument to operate.The reliability of the first unit is 0.9 and that of the second unit is 0.8. The instrument is tested & fails. The probability that only the first unit failed & the second unit is sound is
View SolutionIf `x phi (x)=underset(5)overset(x)int(3t^(2)-2phi(t))dt,x gt-2` and `phi(0)=4` then `phi(2)` is __________
View SolutionA point z moves in the complex plane such that art `(z-2)/(z+2)=(pi)/(4)` then the minimum value of `|z-9sqrt(2)-2i|^(2)` is equal to ____________
View SolutionThe square of the distance of the point of intersection of the line and the plane `(x-1)/(2)=(y-2)/(3)=(z+1)/(6)` and the plane 2x-y+z=6 from the point (- 1, -1, 2) is_________
View SolutionThe number of six letter words (with or without meaning), formed using all the letters of the word 'VOWELS', so that all the consonants never come together, is____________
View SolutionIf the variable line `3x + 4y= alpha` lies between the two circles `(x-1)^(2)+(y-1)^(2)` = 1 and `(x - 9)^(2) + (y-1)^(2) = 4`, without intercepting a chord on either circle, then the sum of all the integral values of `alpha` is__________
View SolutionLet the points of intersections of the lines `x -y +1 = 0, x -2y + 3 = 0 and 2x -5y + 11 = 0`are the mid points of the sides of a triangle ABC. Then the area of the triangle ABC is _______ .
View Solutionlf the sum of the coefficients in the expansion of `(x + y)^n` is 4096, then the greatest coefficient in the expansion is __________.
View SolutionLet X be a random variable with distribution.
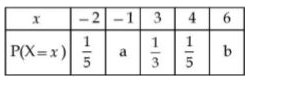
If the mean of X is 2.3 and variance of X is `sigma^2, " then " 100 sigma^2` is equal to :
View SolutionLet [t] denote the greatest integer `lt t`. The number of points where the function `f(x) = [x]abs(x^2-1) + sin (pi/([x] + 3)) - [x + 1], x in (-2, 2)` is not continuous is _________.
View SolutionAll the arrangements, with or without meaning, of the word FARMER are written excluding any word that has two R appearing together. The arrangements are listed serially in the alphabetic order as in the English dictionary. Then the serial number of the word FARMER in this list is _________ .
View SolutionIf for the complex numbers z satisfying `abs(z - 2 -2i) lt 1,` the maximum value of `abs(3iz +6)` is attained at `a + ib, " then " a +b ` is equal to ________.
View SolutionLet `vec a = 2hati - hatj + 2hatk and vecb = hati + 2hatj - hatk`. Let a vector `vecv` be in the plane containing `veca and vec b.` If `vec v` is perpendicular to the vector `3 hati + 2hatj - hatk` and its projection on `vec a` is 19 units, then `abs(2vec v)^2` is equal to _________.
View SolutionLet `f(x) = x^6 + 2x^4 + x^3 + 2x + 3, x in R`. Then the `n` natural number for which `lim_(x to 1) (x^nf(1) - f(x))/(x-1) = 44` is _______.
View SolutionLet f(x) be a polynomial of degree 3 such that `f(k) = - 2/k" for " k = 2, 3,4, 5`. Then the value of `52 - 10 f(10)` is equal to __________.
View SolutionA man starts walking from the point P( -3, 4), touches the x-axis at R, and then turns to reach at the point Q(0, 2). The man is walking at a constant speed. If the man reaches the point Q in the minimum time, then `50 ((PR)^2 + (RQ)^2)` is equal to __________ .
View Solution
Mathematics (Section B) questions and complete solutions for chapter JEE MAINS 2021 of JEE MAINS PREVIOUS YEAR of Class 12