Complete Solutions to Solved Examples of chapter INTRODCTION TO 3D GEOMETRY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | INTRODCTION TO 3D GEOMETRY |
| KC SINHA | Solved Examples |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
Name the octants in which the following points lie : (3,-1,-2)
View SolutionName the octants in which the following points lie : (-3,-1,-2)
View SolutionName the octants in which the following points lie : (3,1,-2)
View SolutionThe coordinates of a point asre e`(-5,-3,2)`. Write down the coordinates of seven points whose absolute values are the same as those of the coordinates of the given point.
View SolutionLet A,B,C be the feet of perpendiculars drawn from a point P to x, y aned z-axses respectively. Find the coordinates of A,B,C if coordinates of P are: (3,1,2)
View SolutionLet A,B,C be the feet of perpendiculars drawn from a point P to x, y aned z-axses respectively. Find the coordinates of A,B,C if coordinates of P are: (3,-6,2)
View SolutionIn the adoining figure if the coordinates of point P are `(a,b,c)` write the coordinates of A,B,C,D,E and F.
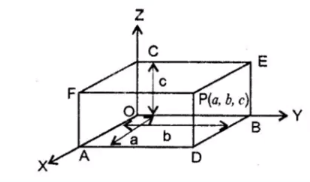
View SolutionWrite down the perpendicular distances of the pont `(x,y,z)` from the three coordinates planes
View SolutionIf O be the origin and OP=r and OP makes an angle `theta` with the positive direction of x-axis and lies in the XY plane find the coordinates of P.
View SolutionFind the reflection of the point `(alpha, beta, gamma)` in the XY-plane, YZ-plane.
View SolutionFind the distance of point (2, -3, -4) from X, Y and Z-axes.
View SolutionPlanes are drawn parallel to the coordinate planes through the points (1,2,3) and (3,-4,-5). Find the lengths of the edges of the parallelopiped so formed.
View SolutionA cube of side 3 units has one vertex at point (1,1,1) and the three edges from this vertex are respectively parallel to positive x-axis and negative y and z-axes. Find the coordinates of other vertices of the cube.
View SolutionFindthe distance between the point `(4,3,-6) and (-2,1,-3)`
View SolutionFind the value of a if the distance between points `P(a,-8,4) and Q(3,-5,4)` is 5.
View SolutionShow that the points (0,7,10),(-1,6,6) and (-4,9,6) form a right angled isosceles triangle .
View SolutionShow by using distane formula that the points (4,5,-5),(0,-11,3) and (2,-3,-1)` are collinear.
View SolutionShow that the coplanar points `(0,4,1),(2,3,-1),(4,5,0) and (2,6,2)` are the vertices of a square.
View SolutionThe coordinates of the point which is equidistant from the points O(0,0,0) A (a,0,0), B(0,b,0) and C(0,0,c)
View SolutionFind the locus of a pont which mioves such that the sum of the of its distances from points `A(0,0-alpha) and B(0,0,alpha)` is constant.
View SolutionFind the coordinates of a point which divides the join of points (3,3,7) and (8,3,2)` internally in the ratio 2:3.
View SolutionFind the co-ordinates of a point which divides the line segment joining the points `A(2,-1,3)` and `B(4,3,1)` in the ratio `3 : 4` externally.
View SolutionFind the ponts of trisectioin of the line segment joinint the points `(2,-2,7) and (5,1,-5)`
View SolutionShow that the three points `A(2,3,4),\ B(-1,2,-3)a n d\ C(-4,1,-10)` are collinear and find the ratio in which C divides AB.
View SolutionDetermine the values of a and b so thast the points `(a,b,3), (2,0,1) and (1,-1,-3)` are colinear.
View SolutionThe vertices f the triangle are `A(5,4,6),\ B(1,-1,3)n a d\ C(4,3,2)dot` The internal bisector of angle A meets BC at D. Find the coordinates of D and the length AD.
View SolutionFind the ratio in which the plane `2x+3y+5z=1` divides the line segment joining the points `(1,0,-3) and (1,-5,7)`.
View SolutionFind the ratio in which the line joining the points `(4,4,-10) and (-2,2,4)` is divided by the XY-plane.
View SolutionIf the points P,Q,R,S are `(4,7,8),(-1,-2,1),(2,3,4) and (1,2,5)` respectively show that PQ and RS intersect. Also find the point of intersection.
View SolutionFind the coordinates of the centroid of the triangle whose vertices are `(x_1,y_1,z_1)`, `(x_2,y_2,z_2)`and `(x_3,y_3,z_3)`.
View SolutionProve analytically that the medians of a triangle are concurrent.
View SolutionTwo vertices of a triangle are `A(3,4,2) and B(1,3,2).` The medians of the triangle intersect at (2,4,3). Find the remaining vertex C of the triangle.
View SolutionThe mid-points of the sides of a triangle are (1, 5, -1),(0,4,-2) and (2, 3, 4). Find its vertices.
View Solution
Solved Examples questions and complete solutions for chapter INTRODCTION TO 3D GEOMETRY of KC SINHA ENGLISH of Class 12