Complete Solutions to Solved Examples of chapter PROPERTIES OF TRIANGLE - FOR COMPETITION of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROPERTIES OF TRIANGLE - FOR COMPETITION |
| KC SINHA | Solved Examples |
| Number Of Questions | 44 |
| Academic Year | 2023-24 |
If in a triangle ABC, `(tanA)/1= (tanB)/2 = (tanC)/3` then prove that `6sqrt(2a)=3sqrt(5b)=2sqrt(10)c`
View SolutionThe sides of a triangle are `x^(2) + x + 1, 2 x + 1, and x^(2) -1`. Prove that the greatest angle is `120^(@)`
View SolutionThe sides of a triangle are three consecutive natural numbers and its largest angle is twice the smalles one. Determine the sides of the triangle.
View SolutionIf in triangle `A BC ,cosAcosB+sinAsinBsinC=1.` Show that `a : b : c=1:1:sqrt(2)`
View SolutionIn ` A B C ,` if `sin^3theta=sin(A-theta)sin(B-theta)sin(C-theta)` , then prove that `cottheta=cot A+cot B+cotCdot`
View SolutionIf in a triangle of base 'a', the ratio of the other two sides is r ( <1).Show that the altitude of the triangle is less than or equal to `(ar)/(1-r^2)`
View SolutionGiven the base of a triangle, the opposite angle A, and the product `k^2` of the other two sides, show that it is not possible for `a` to be less than `2ksinA/2`
View SolutionIn a triangle ABC, the vertices A,B,C are at distances of p,q,r fom the orthocentre respectively. Show that ` aqr+brp+cpq=abc`
View SolutionProve that a triangle `A B C` is equilateral if and only if `tanA+tanB+tanC=3sqrt(3)dot`
View SolutionIf the sides of triangle `ABC` are in G.P with common ratio `r (r<1)`, show that `r<1/2(sqrt5+1)`
View SolutionIf in a triangle `r_1=r_2+r_3+r ,` prove that the triangle is right angled.
View SolutionIf `A+B+C=pi`, prove that
(a) `tan 3A+tan3B+tan3C=tan3A tan 3B tan 3C`
(b) `cot""(A)/(2)+cot""(B)/(2)+cot""(C)/(2)=cot""(A)/(2)cot""(B)/(2)cot""(C)/(2)`
View Solutionabout to only mathematics
View SolutionProve that the sum of the radii of the radii of the circles, which are, respectively, inscribed and circumscribed about a polygon of `n` sides, whose side length is `a ,` is `1/2acotpi/(2n)dot`
View SolutionThe sides of a quadrilateral are 3, 4, 5 and 6 cms. The sum of a pair of opposite angles is `120^0. Show that the area of the quadrilateral is `3sqrt(30)` sq.cm.
View SolutionThe two adjacent sides of a cyclic quadrilateral are 2 and 5 and the angle between them is `60^(@)`. If the area of the quadrilateral is `4 sqrt3`, find the remaining two sides
View SolutionA cyclic quadrilateral `A B C D` of areal `(3sqrt(3))/4` is inscribed in unit circle. If one of its side `A B=1,` and the diagonal `B D=sqrt(3),` find the lengths of the other sides.
View SolutionIn a cyclic quadrilateral ABCD, prove that `tan ^(2)""(B)/(2)=((s-a)(s-b))/((s-c)(s-d)),a,b,c, and d` being the lengths of sides ABC, CD and DA respectively and s is semi-perimeter of quadrilateral.
View SolutionIn triangle ABC, prove that `sin""(A)/(2)sin""(B)/(2)sin""(C)/(2)le(1)/(8)` and hence, prove that `co sec ""(A)/(2)+co sec""(B)/(2)+co sec""(C)/(2)ge6`.
View SolutionThe side of a triangle inscribed in a given circle subtends angles `alpha,betaa n dgamma` at the centre. The minimum value of the arithmetic mean of `cos(alpha+pi/2),cos(beta+pi/2)` , and `cos(gamma+pi/2)` is equal to ____
View SolutionIf A +B+C=`pi`, prove that `tan^(2)""(A)/(2)+tan^(2)""(B)/(2)+tan^(2)""(C)/(2)ge1`
View SolutionLet `1 lt m lt 3. ln a Delta ABC, if 2b= (m+1) a and cos A=1/2 sqrt(((m-1)(m+3))/(m)),` prove that there are two values to the third side, one of which is m times the other.
View SolutionLet A,B,C, be three angles such that `A=pi/4` and `tanB ,tanC=pdot` Find all possible values of `p` such that `A , B ,C` are the angles of a triangle.
View SolutionTwo sides of triangle are of lengths `sqrt(6)` and 4 and the angle opposite to smaller side is `30^(@)`, then how many such triangles are possible ?
View SolutionIf the angle `A ,Ba n dC` of a triangle are in an arithmetic propression and if `a , ba n dc` denote the lengths of the sides opposite to `A ,Ba n dC` respectively, then the value of the expression `a/csin2C+c/asin2A` is (a) `1/2` (b) `(sqrt(3))/2` (c) `1` (d) `sqrt(3)`
View SolutionLet `A B C D` be a quadrilateral with area `18` , side `A B` parallel to the side `C D ,a n dA B=2C D` . Let `A D` be perpendicular to `A Ba n dC D` . If a circle is drawn inside the quadrilateral `A B C D` touching all the sides, then its radius is `a = 3` (b) 2 (c) `3/2` (d) 1
View SolutionOne angle of an isosceles triangle is `120^0` and the radius of its incricel is `sqrt(3)dot` Then the area of the triangle in sq. units is `7+12sqrt(3)` (b) `12-7sqrt(3)` `12+7sqrt(3)` (d) `4pi`
View SolutionA triangle `A B C` with fixed base `B C` , the vertex `A` moves such that `cosB+cosC=4sin^2A/2dot` If `a ,ba n dc ,` denote the length of the sides of the triangle opposite to the angles `A , B ,a n dC` , respectively, then (a)`b+c=4a` (b) `b+c=2a` (c)the locus of point `A` is an ellipse (d)the locus of point `A` is a pair of straight lines
View SolutionInternal bisector of `angle A ` of `Delta ABC` meets side BC to D. A line drawn through D perpendicular to AD intersects the side AC at E and side AB at. F. If a,b,c represent sides of `Delta ABC,` then
View SolutionIf in a `/_\ ABC, cosA.cosB+sinA.sinB.sinC =1,then` (A) `A=B` (B) `C=pi/2` (C) `AC=BC` (D) `AB=sqrt(2) AC`
View SolutionIn a `DeltaABC`, if `r=r_2+r_3-r_1` and `Agt pi/3` then range of `s/a` contains
(A) `(1/2, 2)`
(B) `[1,2)`
(C) `(1/2, 3)`
(D) `(3,oo)`
View SolutionLet us consider a triangle ABC having BC=5 cm, CA=4cm, AB=3cm, D,E are points on BC such BD = DE= EC, `angleCAE=theta`, then:
`AE^(2)` is equal to
View SolutionIn triangle ABC, `R (b + c) = a sqrt(bc)`, where R is the circumradius of the triangle. Then the triangle is
View SolutionIn acute angled triangle `A B C ,A D` is the altitude. Circle drawn with `A D` as its diameter cuts `A Ba n dA Ca tPa n dQ ,` respectively. Length of `P Q` is equal to `/(2R)` (b) `(a b c)/(4R^2)` `2RsinAsinBsinC` (d) Δ`/R`
View SolutionStatement 1. If `A` is the area and `2s` is the perimeter of a `/_\ABC`, then `Ale s^2/(3sqrt(3))`,
Statement 2. `A.M ≥ G.M.`
(A) Both Statements are false
(B) Both Statement 1 and Statement 2 are true
(C) Statement 1 is true but Statement 2 is false.
(D) Statement 1 is flse but Stastement 2 is true
View SolutionRadius of circumcircle of `/_\DEF` is
`(A) R`
`(B)` `R/2`
`(C)` `R/4`
`(D)` none of these
View SolutionIf `cotA+cotB+cotC``=``k(1/x^2+1/y^2+1/z^2)` then the value of `k` is
`(A)` `R^2`
`(B)` `2R`
`(C)` `/_\`
`(D)`a^2+b^2+c^2`
View SolutionLet `A B Ca n dA B C '` be two non-congruent triangles with sides `A B=4,A C=A C^(prime)=2sqrt(2)` and angle `B=30^0` . The absolute value of the difference between the areas of these triangles is
View SolutionABC is a triangle. Its area is 12 sq. cm. and base is 6 cm. the difference of base angle is `60^0`. If A be the angle opposite to the base, then the value of `8sinA-6cosA` is……
View Solutionperpendiculars are drawn from the angles `A , Ba n dC` of an acute-angled triangle on the opposite sides, and produced to meet the circumscribing circle. If these produced parts are `alpha,beta,gamma` , respectively, then show that `a/alpha+b/beta+c/gamma=2(tanA+tanB+t a nC)dot`
View SolutionThe sides of a triangle are in AP. If the angles A and C are the greatest and smallest angle respectively, then `4 (1- cos A) (1-cos C)` is equal to
View SolutionThe radius of the circle passing through the vertices of the triangle ABC, is
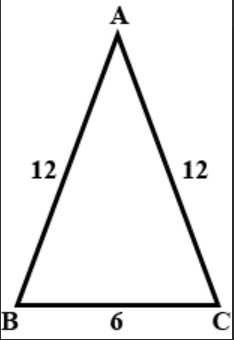
View SolutionThree circles touch one another externally. The tangents at their points of contact meet at a point whose distance from a point of contact is 4. Find the ratio of the product of the radii to the sum of the radii of the circles.
View SolutionBisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are `90o-1/2A` ,`90o-1/2B` and `90o-1/2C`
View Solution
Solved Examples questions and complete solutions for chapter PROPERTIES OF TRIANGLE - FOR COMPETITION of KC SINHA ENGLISH of Class 12