Complete Solutions to Exercise of chapter PROPERTIES OF TRIANGLE - FOR COMPETITION of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROPERTIES OF TRIANGLE - FOR COMPETITION |
| KC SINHA | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A ring,10 cm in diameter, is suspended from a point 12cm above its centre by 6 equal strings attached to its circumference at equal intervals. Find the cosine of the angle between consecutive strings.
View SolutionIf the angles of a triangle are in the ratio `7:2:1,` then prove that the ratio of smallest side to the largest side is `sqrt5-1:sqrt5+1.`
View SolutionIf the base angles of triangle are `(22)/(12)a n d112 1/2^0` , then prove that the altitude of the triangle is equal to `1/2` of its base.
View SolutionIf f,g,h are internal bisectoirs of the angles of a triangle ABC, show that `1/f cos, A/2+ 1/g cos, B/2+1/h cos, C/2= 1/a+1/b+1/c`
View SolutionThe rational number which equals the number `2. 357 ` with recurring decimal is `(2355)/(1001)` b. `(2379)/(997)` c. `(2355)/(999)` d. none of these
View SolutionA triangle side are few `7 cm, 4sqrt3 cm` and` sqrt(13) cm` then the smallest angle is
View SolutionIn an isosceles right angled triangle , a straight line drwan from the mid - point of one of equal sides to the opposite angle . It divides the angle into two parts , `theta and (pi//4-theta)` . Then `tan theta and tan [(pi//4) -theta]` are equal to
View SolutionIf the roots of the equation `x^(3) - px^(2) + qx - r = 0` are in A.P., then
View SolutionIn any `!ABC , (Sigma)((sin^(2)A+sinA+1)/(sinA))` is always greater than
View SolutionIn a `triangle ABC,` `sin^4A+sin^4B+ sin^4C=3/2+2cosAcosBcosC+1/2cos2Acos2Bcos2C`
View SolutionIf any triangle `A B C` , that: `(asin(B-C))/(b^2-c^2)=(bsin(C-A))/(c^2-a^2)=(csin(A-B))/(a^2-b^2)`
View SolutionIn any triangle `A B C` prove that: `sin((B-C)/2)=((b-c)/a)cosA/2`
View SolutionIf in a `!ABC ,`
`sin^(3)A+sin^(3)B+sin^(3)C=3sinAsinBsinC`, then
`abs({:(a,b,c),(b,c,a),(c,a,b):})`
View SolutionIn a triangle ABC, Prove that: `sin^3A+sin^3B+sin^3C= 3cos, A/2 cos, B/2 cos, C/2 +cos, (3A)/2 cos, (3B)/2 cos, (3C)/2`
View SolutionProve that `(cotA/2+cotB/2)(asin^2B/2+bsin^2A/2)=ccotC/2`
View SolutionIf `pa n dq` are perpendicular from the angular points A and B of ` A B C` drawn to any line through the vertex `C ,` then prove that `a^2b^2sin^2C=a^2p^2+b^2q^2-2a b p qcosCdot`
View SolutionLet O be a point inside a triangle ABC such that `/_OAB = /_OBC = /_OCA = omega,` then Show that:
View SolutionIf `x,y,z` are respectively perpendiculars from the circumcentre on the sides of the `DeltaABC`, the value of `a/x+b/y+c/z-(abc)/(4xyz)=`
View SolutionProve that a triangle ABC is equilateral if and only if `tanA+tanB+tanC=3sqrt(3).
View SolutionIn a triange ABC, if `sin(A/2) sin (B/2) sin(C/2) = 1/8` prove that the triangle is equilateral.
View SolutionIf the sides of triangle in A.P. and `LC=90+LA` then prove that sides will be in ratio `sqrt7+1:sqrt7:sqrt7-1`
View SolutionIf in a triangle `A B C ,cosA+2cosB+cosC=2` prove that the sides of the triangle are in `AP`
View SolutionIn a triangle ABC, if `(a-b)/(b-c)= (s-a)/(s-c)`, then `r_1,r_2,r_3` are in
View Solution. In a `DeltaABC, If tan (A/2) , tan(B/2), tan (C/2)`, are in H.P.,then a,b,c are in
View SolutionIf the sides of triangle in A.P. and `LC=90+LA` then prove that sides will be in ratio `sqrt7+1:sqrt7:sqrt7-1`
View SolutionIf the sides a,b,c of a triangle are in Arithmetic progressioni then find the value of `tan, A/2+tan, C/2` in terms of `cot, B/2`
View SolutionProve that `r_1+r_2+r_3-r=4R`
View Solution`prove that : triangle ABC, 1/r_1+1/r_2+1/r_3=1/r`
View Solution` prove that : 1/r^2+1/r_1^2+1/r_2^2+1/r_3^2=(a^2+b^2+c^2)/ /_\^2 `
View SolutionIf `A,A_1,A_2` and `A_3` are the areas of the inscribed and escribed circles of a triangle, prove that `1/sqrtA=1/sqrt(A_1)+1/sqrt(A_2)+1/sqrt(A_3)`
View SolutionProve that : `(r_1)/(b c)+(r_2)/(c a)+(r_3)/(a b)=1/r-1/(2R)`
View SolutionABC is an isosceles triangle inscribed in a circle of radius `rdot` If `A B=A C` and `h` is the altitude from `A` to `B C ,` then triangle `A B C` has perimeter `P=2(sqrt(2h r-h^2)+sqrt(2h r))` and area A= ____________ and = __________ and also `("lim")_(xvec0)A/(P^3)=______`
View SolutionIf `p_1,p_2,p_3` re the altitudes of the triangle ABC from the vertices A, B and C respectivel. Prove that `(cosA)/p_1+(cosB)/p^2+(cosC)/p_3 =1/R`
View SolutionThree circles whose radii are a,b and c and c touch one other externally and the tangents at their points of contact meet in a point. Prove that the distance of this point from either of their points of contact is `((abc)/(a+b+c))^(1/2)`.
View SolutionIn a triangle ABC prove that `r_1r_2r_3=r^3 cot^2 (A/2). cot^2 (B/2).cot^2(C/2)`
View SolutionProve that : `(r_1+r_2) tan (C )/(2) = (r_3- r) cot ( C)/(2) = c`
View SolutionProve that : `4\ R\ s in AsinB\ s in C=acosA+b\ cos B+ccosCdot`
View Solution`(r_1-r)(r_2-r)(r_3-r)=4R r^2`
View SolutionIn a triangle ABC, prove that `r^2+r_1^2+r_2^2+r_3^2=16R^2-a^2-b^2-c^2.`
View SolutionIf 1 is the incentre and `1_1,1_2,1_3` are the centre of escribed circles of the `triangleABC`. Prove that
`II_1,II_2,III_3 = 16 R^2r`.
View SolutionIf 1 is the incentre and `1_1,1_2,1_3` are the centre of escribed circles of the `triangleABC`. Prove that
`II_1,II_2,III_3 = 16 R^2r`.
View Solution`1/(bc)+1/(ca)+1/(ab)=`
View Solution`(r_1)/((s-b)(s-c))+(r_2)/((s-c)(s-a))+(r_3)/((s-a)(s-b))=3/r`
View SolutionIf the distances of the vertices of a triangle =ABC from the points of contacts of the incercle with sides are `alpha,betaa n dgamma` then prove that `r^2=(alphabetagamma)/(alpha=beta+gamma)`
View SolutionIf in a triangle `(1-(r_1)/(r_2))(1-(r_1)/(r_3))=2` then the triangle is right angled (b) isosceles equilateral (d) none of these
View SolutionIn a triangle ABC, prove that the ratio of the area of the incircle to that of the triangle is `pi:cot(A/2) cot(B/2) cot(C/2)`
View SolutionFor a regular polygon, let r and R be the radii of the inscribed and the circumscribed circles. A false statement among the following is There is a regular polygon with `r/R=1/(sqrt(2))` (17) There is a regular polygon with `r/R=2/3` (30) There is a regular polygon with `r/R=(sqrt(3))/2` (47) There is a regular polygon with `r/R=1/2` (60)
View SolutionA square whose side is 2 cm, has its corners cut away so as to form a regular octagon, find its area.
View SolutionAn equilateral triangle and a regular hexagon has same perimeter. Find the ratio of their areas.
View SolutionThe ratio of the area of a regular polygon of `n` sides inscribed in a circle to that of the polygon of same number of sides circumscribing the same is 3:4. Then the value of `n` is 6 (b) 4 (c) 8 (d) 12
View SolutionA cyclic quadrilateral `A B C D` of areal `(3sqrt(3))/4` is inscribed in unit circle. If one of its side `A B=1,` and the diagonal `B D=sqrt(3),` find the lengths of the other sides.
View SolutionIf the number of sides of two regular polygons having the same prerimeter be `n and 2n` respectiely, prove that their areas are in the ratio `2cos pi/n: (1+cos pi/n)`
View SolutionIn a `DeltaABC`, the median to the side BC is of length `1/sqrt(11-6sqrt3)` and it divides the `angleA` into angles `30^@` and `45@.` Find the length of the side BC.
View SolutionIn an acute-angled triangle ABC, `tanA+tanB+tanC`
View SolutionIf in a triamgle ABC, `theta` is the angle determined by `cos theta=(a-b)//c`, then
View SolutionIf R be the circum radius and r the in radius of a triangle ABC, show that `Rge2r`
View SolutionIf `cosA=tanB,cosB=tanCand cosC=tanA,`
Show that `sinA=sinB=sinC=2*sin18^o`
View SolutionIf `A+B+C=pi`, prove that: `cot^2 A+cot^2 B + cot^2 C ge 1`
View SolutionIn acute angled `triangle ABC` prove that `tan ^(2)A+tan^(2)B+tan^(2)Cge9`.
View SolutionIn `DeltaABC`, prove that `"cosec"(A)/(2)+"cosec"(B)/(2)+"cosec"(C)/(2) ge 6` .
View SolutionProve that in `triangle ABC, cos A B cos Cle(1)/(8)`.
View SolutionThree equal circles each of radius `r` touch one another. The radius of the circle touching all the three given circles internally is `(2+sqrt(3))r` (b) `((2+sqrt(3)))/(sqrt(3))r` `((2-sqrt(3)))/(sqrt(3))r` (d) `(2-sqrt(3))r`
View SolutionIn a`DeltaABC`, prove that
`underset(r=0)overset(n)Sigma .^(n)C_(r)a^(r)b^(n-r) cos ( r B-(n-r)A)=c^(n)`.
View SolutionIf `triangle` is the area and 2s is the perimeter of `triangleABC`, then prove that `triangle le s^(2)/(3sqrt(3))`
View SolutionThe sides of a triangle are `3x + 4y, 4x + 3y` and `5x+5y` units, where `x gt 0, y gt 0`. The triangle is
View SolutionIn a `/_\ABC , cosec A[sinB.cosC+cosB.sinC]=`
(A) `c/a`
(B) `a/c`
(C) 1
(D) none of these
View SolutionIf the data given to construct a triangle ABC are a = 5, b= 7, sin `A=3//4`, then it is possible to construct
View SolutionIf the angles of a triangle are in the ratio 1:2:3,the corresponding sides are in the ratio
View SolutionIf three sides a,b,c of a triangle ABC are in arithmetic progression, then the value of `cot, A/2, cot, C/2` is (A) 1 (B) 2 (C) 3 (D) None of these
View SolutionIf `b=3,c=4,a n dB=pi/3,` then find the number of triangles that can be constructed.
View SolutionIn a triangle `A B C ,a=4,b=3,/_A=60^0` then `c` is root of the equation `c^2-3c-7=0` (b) `c^2+3c+7=0` (c) `c^2-3c+7=0` (d) `c^2+3c-7=0`
View SolutionIf in a triangle `ABC, 3 sin A = 6 sin B=2sqrt3sin C`, then the angle A is
View SolutionThe number of triangles `ABC` that can be formed with `sinA=5/(13), a=3` and `b=8` is
View SolutionThe lengths of the sides of a triangle are `alpha-beta, alpha+beta` and `sqrt(3alpha^2+beta^2), (alpha>beta>0)`. Its largest angle is
View SolutionIn a `Delta PQR` (as shown in figure) if `x:y:z=2:3:6`, then the value of `angle QPR` is :
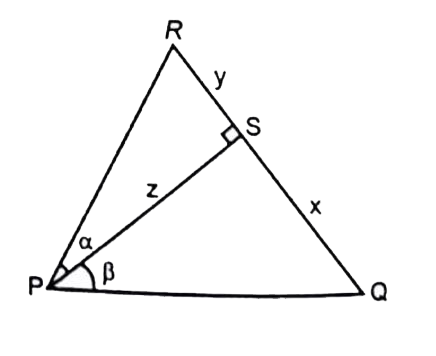
View SolutionIf in `Delta`ABC ,`/_c=90^0` then the maximum value of sinAsinB is
View SolutionIn an isosceles right angled triangle ABC, `/_B=90^0, AD` is the median then `(sin/_BAD)/(sin/_CAD)` is (A) `1/sqrt(2)` (B) `sqrt(2)` (C) 1 (D) none of these
View SolutionIf in a `DeltaABC`, c = 3b and C - B = 90°, then tanB=
View SolutionIf the lengths of the sides of a triangle are `3, 5, 7`, then its largest angle of the triangle is
View SolutionIn a `!ABC` if a = 7 , b = 8 and c = 9 , then the length of the line joining B to the mid-points of AC is
View SolutionIf H is the orthocenter of `DeltaABC` and if `AH = x, BH = y, CH = z`, then `a/x+b/y+c/z=`
View SolutionIf the sides of a triangle are in the ratio `3 : 7 : 8`, then find `R : r`
View SolutionIf in a` /_\ABC, sin^2A+sin^2B+sin^2C=2, then /_\ `is always a an (A) isosceles triangle (B) right angled triangle (C) acute angled triangle (D) obtuse angled triangle
View SolutionFor a`/_\ABC, if cotA.cotB.cotCgt0`, then nature of the triangle is
(A) acute angled triangle
(B) right angled triangle
(C) obtuse angled triangle
(D) none of these
View SolutionIf the sides of a triangle are in G.P., and its largest angle is twice the smallest, then the common ratio `r` satisfies the inequality `0
View SolutionIf in a `/_\ABC, a^2cos^2A=b^2+c^2,` then angle A is (A) less than `45^0` (B) more than of `45^0 and less than 90^0` (C) right angled (D) obtuse angle
View SolutionThe perimeter of a `Delta ABC` is 6 times the A.M. of the sines of its angles. If the side 'a' is 1, then the angle A is
View SolutionIf angle C of a triangle ABC be obtuse, then (A) `0 < tan A tan B < 1` (B) `tan A tan B > 1` (C) `tan A tan B=1` (D) none of these
View SolutionIn an equilateral triangle, inradius `r ,` circumradius `R` and ex-radius `r_1` are in
View SolutionThe ratio of the area of triangle inscribed in ellipse `(x^2)/(a^2)+(y^2)/(b^2)=1` to that of triangle formed by the corresponding points on the auxiliary circle is 0.5. Then, find the eccentricity of the ellipse.
View SolutionIf in a triangle ABC, the altitude AM be the bisector of `/_BAD`, where D is the mid point of side BC, then prove that `(b^2-c^2)= (a^2)/(2)`.
View SolutionIn a `/_\ABC, tan, A/2 = 5/6 and tan, C/2 = 2/5 then (A) a,c,b are in A.P. (B) a,b,c are in A.P. (C) b,a,c are in A.P. (D) a,b,c are in G.P.
View SolutionThe sides of a triangle are `3x + 4y, 4x + 3y` and `5x+5y` units, where `x gt 0, y gt 0`. The triangle is
View SolutionIn triangle `A B C ,A D` is the altitude from `Adot` If `b > c ,/_C=23^0,a n dA D=(a b c)/(b^2)-c^2,` then `/_B=_____`
View SolutionA circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in this circle is (A) `a^2/12` (B) `a^2/6` (C) `a^2/3` (D) `2a^2`
View SolutionLet `A_0A_1A_2A_3A_4A_5` be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths the line segments `A_0A_1, A_0A_2` and `A_0A_4` is
View SolutionLet `f(x+y)=f(x).f(y)` for all x and y and `f(1)=2.` If in as triangle ABC, `a=f(3), b=f(1)+f(3), c=f(2)+f(3), then 2A=` (A) C (B) 2C (C) 3C (D) 4C
View SolutionIn a triangle ABC the angle B is greater than angle C. If the measure of angles B and C satisfy the equation `4sin^3x-3sinx+0.75=0` then the measure of angle A is (A) `pi/2` (B) `(2p)/3` (C) `pi/6` (D) `(5pi)/6`
View SolutionIn a `triangle ABC`, `angleB=pi/3`, `angleC=pi/4` and D divides `BC` internally in the ratio `1 : 3` Then `(angleBAD)/(angleCAD)=` is equal to (a) `1/sqrt6` (b) `1/3` (c) `1/sqrt3` (d) `sqrt(2/3)`
View SolutionIf a, b,c be the sides foi a triangle ABC and if roots of equation `a(b-c)x^2+b(c-a)x+c(a-b)=0` are equal then `sin^2 A/2, sin^2, B/2, sin^2 C/2` are in (A) A.P. (B) G.P. (C) H.P. (D) none of these
View Solution
Exercise questions and complete solutions for chapter PROPERTIES OF TRIANGLE - FOR COMPETITION of KC SINHA MATHS (HINGLISH) of Class 12