Complete Solutions to प्रश्नावली 13(D) of chapter प्रायिकता of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | प्रायिकता |
| MANOHAR RAY | प्रश्नावली 13(D) |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
जाँच कीजिए कि प्रायिकता बटनों में कौन से एक यादृच्छिक चर के लिये सम्भव है | कारण सहित उत्तर दीजिए-
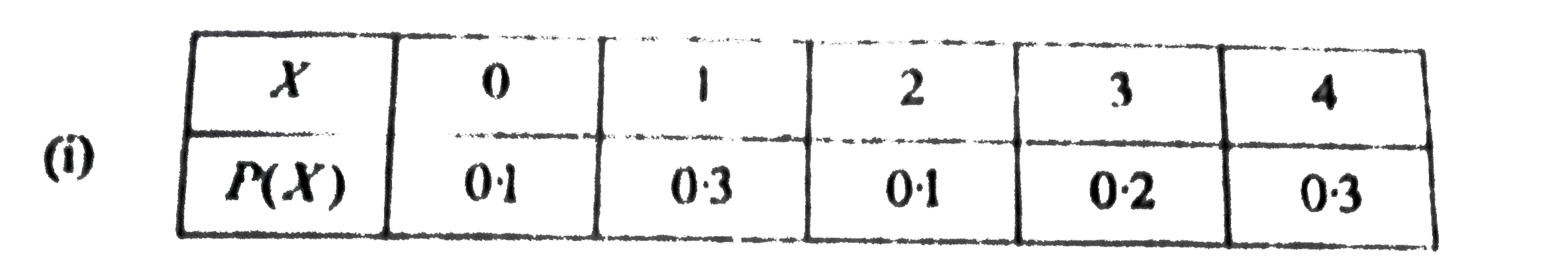
View Solutionजाँच कीजिए कि प्रायिकता बटनों में कौन से एक यादृच्छिक चर के लिये सम्भव है | कारण सहित उत्तर दीजिए-
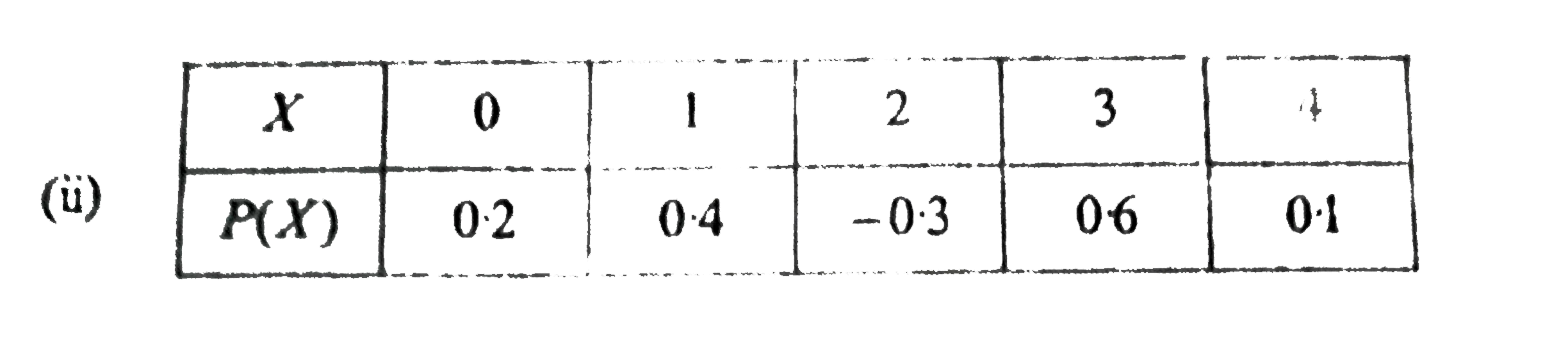
View Solutionजाँच कीजिए कि प्रायिकता बटनों में कौन से एक यादृच्छिक चर के लिये सम्भव है | कारण सहित उत्तर दीजिए-
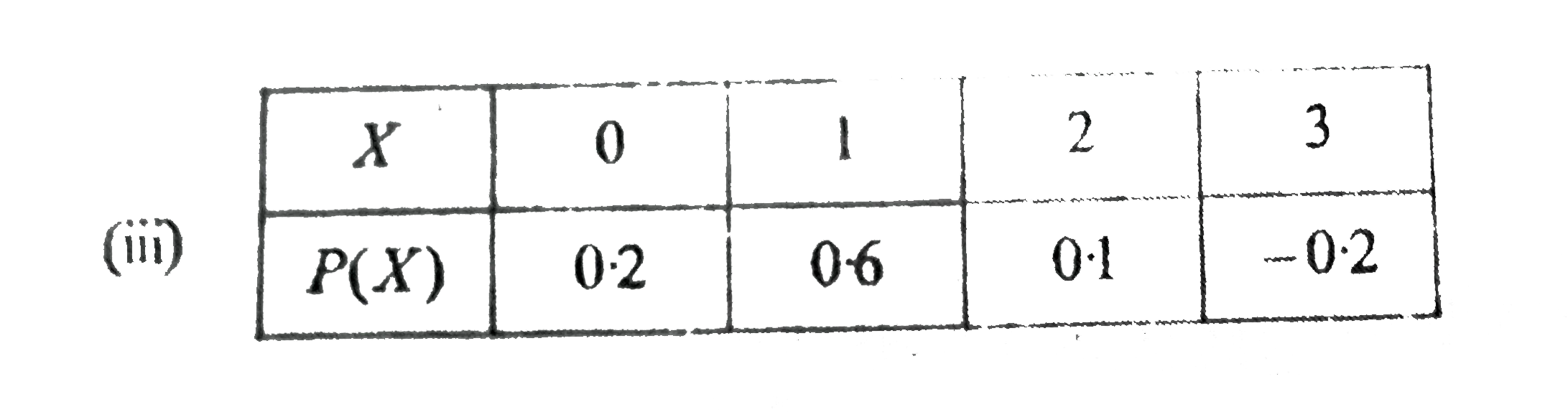
View Solutionजाँच कीजिए कि प्रायिकता बटनों में कौन से एक यादृच्छिक चर के लिये सम्भव है | कारण सहित उत्तर दीजिए-
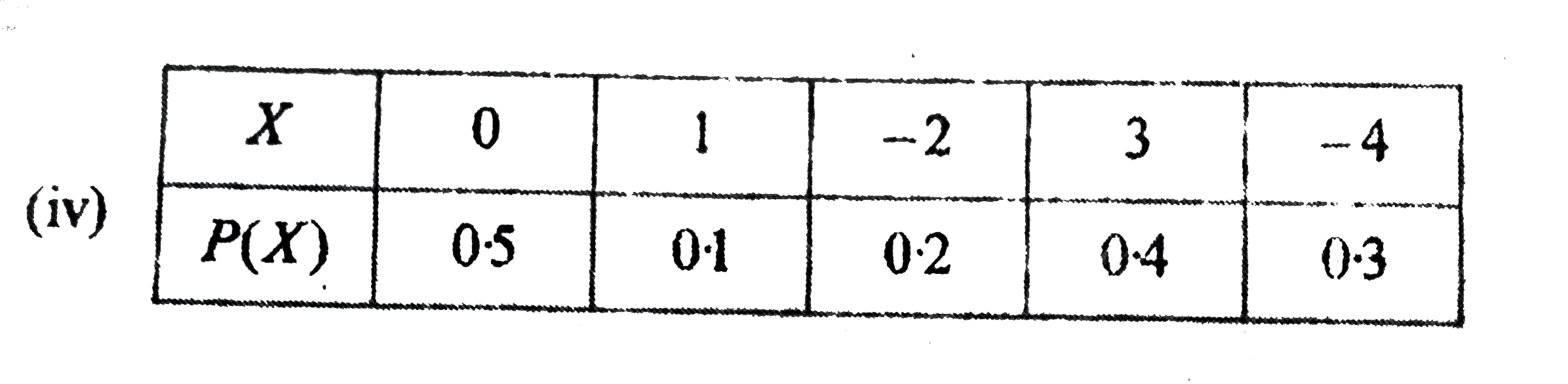
View Solutionजाँच कीजिए कि प्रायिकता बटनों में कौन से एक यादृच्छिक चर के लिये सम्भव है | कारण सहित उत्तर दीजिए-
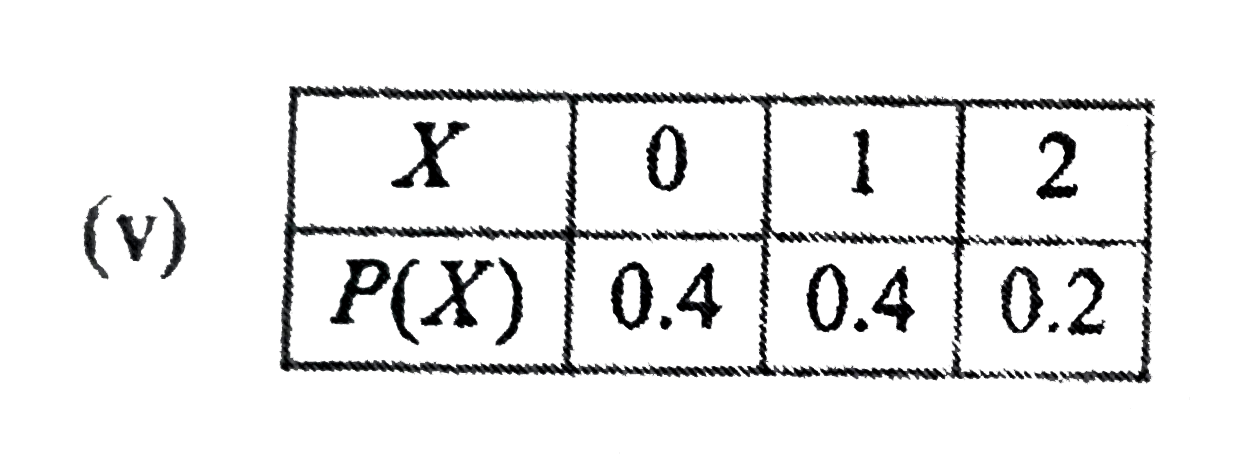
View Solutionजाँच कीजिए कि प्रायिकता बटनों में कौन से एक यादृच्छिक चर के लिये सम्भव है | कारण सहित उत्तर दीजिए-
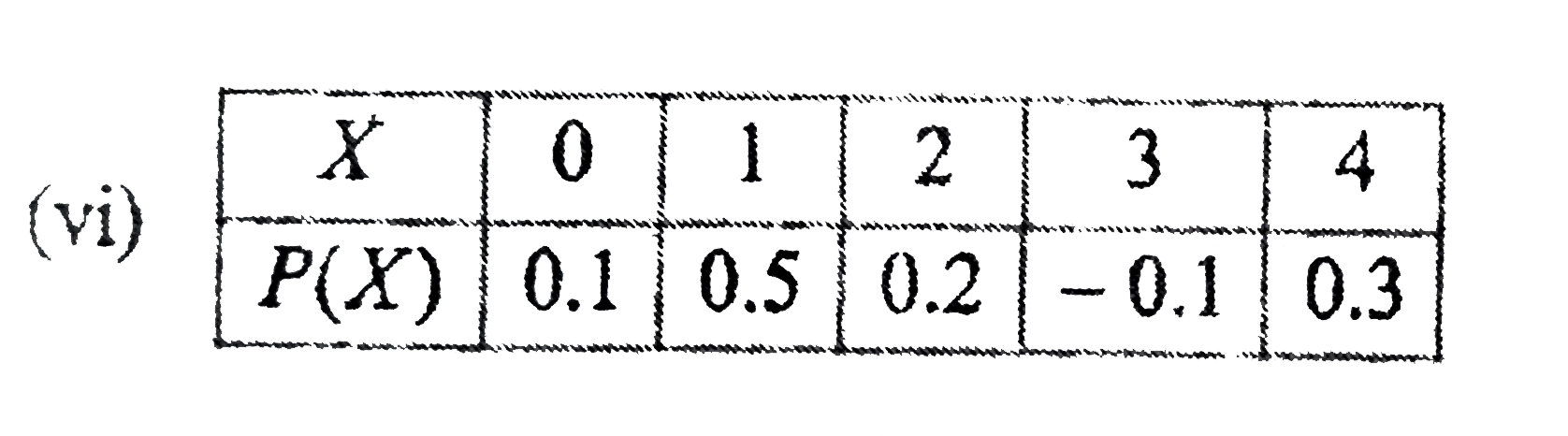
View Solutionजाँच कीजिए कि प्रायिकता बटनों में कौन से एक यादृच्छिक चर के लिये सम्भव है | कारण सहित उत्तर दीजिए-
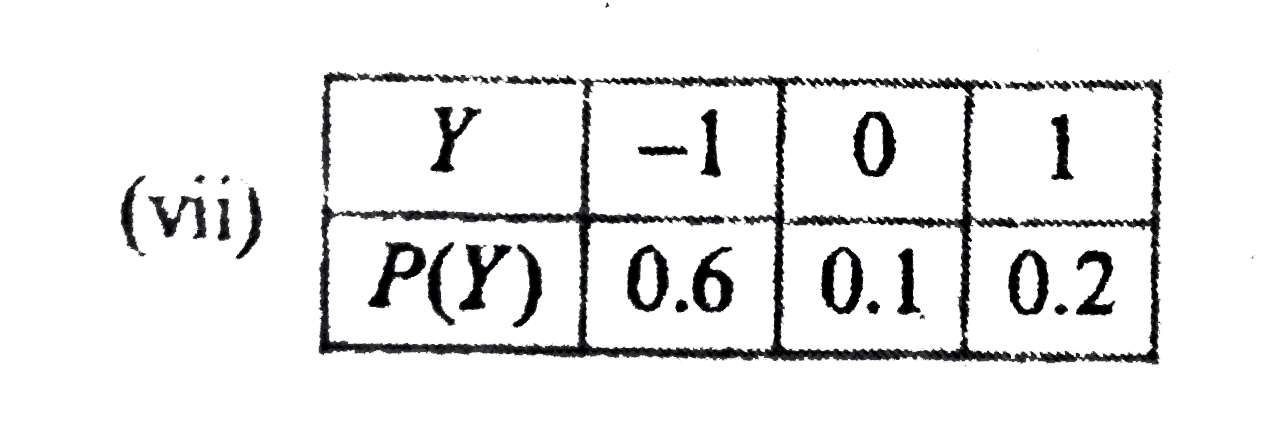
View Solutionजाँच कीजिए कि प्रायिकता बटनों में कौन से एक यादृच्छिक चर के लिये सम्भव है | कारण सहित उत्तर दीजिए-

View Solution(i) एक कलश में 5 लाल और 2 काली गेंद है | दो गेंदे यादृच्छया निकाली गई | मान लीजिए X काली गेंदों की संख्या को व्यक्त करता है X के संभावित मान क्या है ? क्या X यादृच्छिक चर है ?
(ii) एक थैले में 6 काली और 2 सफेद गेंदे है | दो गेंदे यादृच्छया निकाली गई | निकाली गयी सफेद गेंदों को X से निरूपित करते है | X के संभावित मान क्या है ? क्या X यादृच्छिक चर है ?
View Solutionएक पाँसे को दो बार उछालने ( या दो पासो को एक साथ उछालने ) में 6 प्राप्त करने की संख्या X का प्रायिकता बंटन ज्ञात कीजिए |
View Solutionनिम्नलिखित की प्रायिकता बंटन ज्ञात कीजिए-
(i) दो सिक्को को एक साथ एक बार उछालने पर पटों की संख्या का |
(ii) एक सिक्के की तीन उछालो में पटों की संख्या का |
(iii) एक सिक्के की दो उछालो में चीतों की संख्या का
(iv) तीन सिक्के को एक साथ एक बार उछालने पर पटों की संख्या का
(v) एक सिक्के की चार उछालो में चीतों की संख्या का
View Solutionयदि दो पाँसो को एक साथ उछाला जाता है, जब सफलताओं का प्रायिकता वितरण ज्ञात कीजिए, जहाँ-
(i) 4 से बड़ी संख्या जिसे सफलता माना गया है |
(ii) कम-से-कम एक पाँसे पर 6 प्रकट होना |
View Solutionएक पासा दो बार उछालने पर सफलता की संख्या का प्रायिकता बंटन ज्ञात कीजिए जहाँ
(i) 4 से बड़ी संख्या को एक सलफता माना गया है |
(ii) पासे से बड़ी संख्या 6 प्रकट होना को एक सफलता माना गया है |
View Solutionएक थैले में 5 सफेद तथा 3 काली गेंदे है | थैले में से गेंदे यादृच्छया निकाली जाती है | काली गेंदों की प्रायिकता बंटन ज्ञात कीजिए |
View Solutionएक यादृच्छिक चर X का प्रायिकता बंटन निम्नलिखित दिया गया है-

(i) k
(ii) `P( X lt 4)`
(iii) `P(X lt 5)`
(iv) `P( X lt 6)`
View Solutionएक यादृच्छिक चर X का प्रायिकता बंटन निचे दिया गया है |
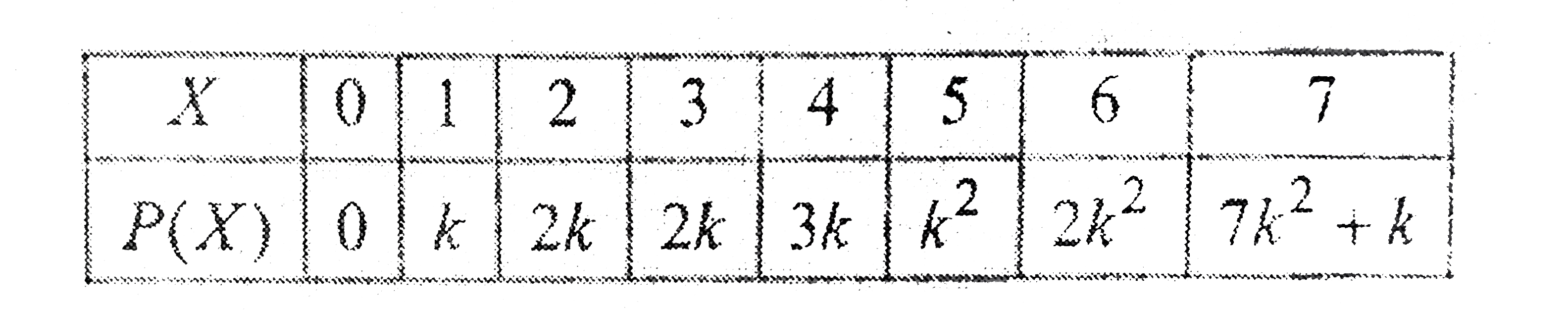
(i) K
(ii) `P( X lt 3)`
(iii) `P( X gt 6)`
(iv) `P( 0 lt X lt 3)`
View Solutionएक यादृच्छिक चार X का प्रायिकता फलन P (x) निम्न प्रकार से हे, जहाँ k कोई संख्या है
`P(x){:{(,k,,"यदि",, x = 0),(,2k,,"यदि",, x = 1),(,3k,,"यदि",,x=2),(,0,,"यदि",,"अन्यथा") :}`
(a) k का मान ज्ञात कीजिए |
(b) `P( X lt 2), P( x le 2), P( X ge 2)` ज्ञात कीजिए |
View Solution52 ताश के पत्तो की एक गड्डी से दो पत्ते बिना प्रतिस्थापन के क्रमशः खींचे गये | बेगम की संख्या होने का प्रायिकता वितरण ज्ञात कीजिए |
View Solutionसाक्षी प्रकार के 15 संतरों में 5 ख़राब संतरे मिला दिये जाते है | दो संतरे निकालने में ख़राब संतरों की संख्या का प्रायिकता बंटन ज्ञात कीजिए |
View Solutionएक पाँसे को तीन बार उछालने पर 6 की संख्या का प्रायिकता बंटन ज्ञात कीजिए | बंटन का मध्य तथा प्रसरण भी ज्ञात कीजिए |
View Solutionएक पाँसे को दो बार उछाला जाता है यह यादृच्छिक उछाल प्राप्त विषम संख्या को सफलता के रूप में परिभाषित करता है | सफलता की संख्या का माध्य और प्रसरण ज्ञात कीजिए |
View Solutionमान लीजिए कि दो पांसों को एक साथ उछाला जाता है | पाँसो पर प्राप्त संख्याओं का योग लिया जाता है | योग प्राप्त होने का प्रायिकता बंटन ज्ञात कीजिए तथा माध्य और प्रसरण और मानक विचलन भी ज्ञात करें |
View Solution30 बल्बों के एक ढेर से, जिसमे 6 बल्ब ख़राब है 4 बल्बों का एक नमूना (प्रतिदर्श ) यादृच्छिक बिना प्रतिस्थापना के निकला जाता है | ख़राब बल्बों की संख्या का प्रायिकता बंटन ज्ञात कीजिए |
View Solutionएक सिक्का समसर्वय संतुलित नहीं है जिसमे चित प्रकट होने की संभावना पट प्रकट होने की संभावना की तीन गुनी है | यदि सिक्का दो बार उछाला जाता है तो पटों की संख्या का प्रायिकता बंटन ज्ञात कीजिए |
View Solutionदो पांसों को युग्मत उछाला गया | यदि X, छक्कों की संख्या को व्यक्त करता है, तो X की प्रत्याशा ज्ञात कीजिए |
View Solutionप्रथम छः धन पूर्णाकों में से दो संख्याएँ यादृच्छया (बिना प्रतिस्थापन ) चुनी गई | मान ले X दोनों संख्याओं में से बड़ी संख्या को व्यक्त करता है E (X) ज्ञात कीजिए |
View Solutionमान लीजिए दो पांसों को फेकने पर प्राप्त संख्याओं के योग को X से व्यक्त किया गया हे | X का प्रसरण और मानक विचलन ज्ञात कीजिए |
View Solutionएक कक्षा में 15 छात्र है जिनकी आयु 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 और 20 वर्ष है | एक छात्र को इस प्रकार चुना गया कि प्रत्येक छात्र के चुने जाने की संभावना समान है और चुने गए छात्र की आयु (X) को लिखा गया | यादृच्छिक चर X का प्रायिकता बंटन ज्ञात कीजिए | X का माध्य, प्रसरण व मानक विचलन भी ज्ञात कीजिए |
View Solutionएक बैठक में 70% सदस्यों ने किसी प्रस्ताव का अनुमोदन किया और 30% सदस्यों ने विरोध किया | एक सदस्य को यादृच्छया चुना गया और यदि उस सदस्य ने प्रस्ताव का विरोध किया हो तो X = 0 लिया गया, जब कि यदि उसने प्रस्ताव का अनुमोदन किया हो तो X = 1 लिया गया | E (X) और var (X) ज्ञात कीजिए |
View Solutionएक व्यक्ति एक न्याय सिक्को को कितनी बार उछालने कि कम से कम एक चित की प्रायिकता 90% से अधिक हो ?
View Solutionएक खेल में किसी व्यक्ति को एक न्याय्य पासे को उछालने के बाद छः प्रकट होने पर एक रुपया मिलता है और अन्य कोई संख्या प्रकट होने पर वह एक रूपया हार जाता है | एक व्यक्ति यह निर्णय लेता है, कि वह पासे को तीन बार फेकेगा लेकिन जब भी छः प्राप्त होगा वह खेलना छोड़ देगा | उसके द्वारा जीती/हारी गयी राशि की प्रत्याशा ज्ञात कीजिए |
View Solution
प्रश्नावली 13(D) questions and complete solutions for chapter प्रायिकता of DR HARSWAROOP SHARMA MATHS (HINDI) of Class 12