Complete Solutions to MULTIPLE CHOICE QUESTION of chapter ROTATIONAL MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| MARVEL | MULTIPLE CHOICE QUESTION |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The physical quantity in translational motion, which is analogous to moment of inertia in rotational motion is
View SolutionTwo masses of 500 gram and 600 grams are attached to the 10 cm and 80 cm marks respectively of a light metre scale. The moment of inertia of this system about an axis passing through the centre of the scale will be
View SolutionA rod 0.5 m long has two masses each of 20 gram stuck at its ends. If the masses are treated as point masses and if the mass of the rod is neglected, then the moment of inertia of the system about a transverse axis passing through the centre is
View SolutionA wheel of mass 10 kg and radius of gyration 50 cm is rotating at 300 rpm. Then, the rotational kinetic energy of the wheel is
View SolutionFour similar point masses (m each) are symmetrically placed on the circumference of a disc of mass M and radius R. Moment of inertia of the system about an axis passing through centre O and perpendicular to the plane of the disc will be
View SolutionAbout which axis, the moment of inertia in the given triangular lamina is maximum?
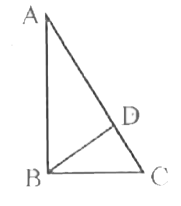
View SolutionThe angular displacement of a flywheel varies with time as `theta = at + bt^(2)-ct^(3)`. Then the angular acceleration is given by
View SolutionA disc of mass 1 kg and radius 10 cm is rotating about its axis with an anuglar velocity of 2 rad/s. The linear momentum of the disc,
View SolutionThree point masses, each of mass `m`, are placed at the corners of an equilateral triangle of side `L`. The moment of inertia of this system about an axis along one side of the triangle is
View SolutionThree thin rods, each of length 2 m and mass 3 kg are placed along x, y and z axes, such that one end of each rod is at the origin. The moment of inertia of this system about the x axis is
View SolutionA circular disc is to be made by using equal masses of aluminium and iron. To get maximum moment of inertia, about its geometrical axis, it should be so prepared that
View SolutionIn first figure a meter stick, half of which is wood and the other half steel is pivoted at the wooden end at `A` and a force is applied at the steel and at `O`. On second figure the stick is pivoted at the steel end at `O` and the same force is applied at the wooden end at `A`. The angular acceleration.
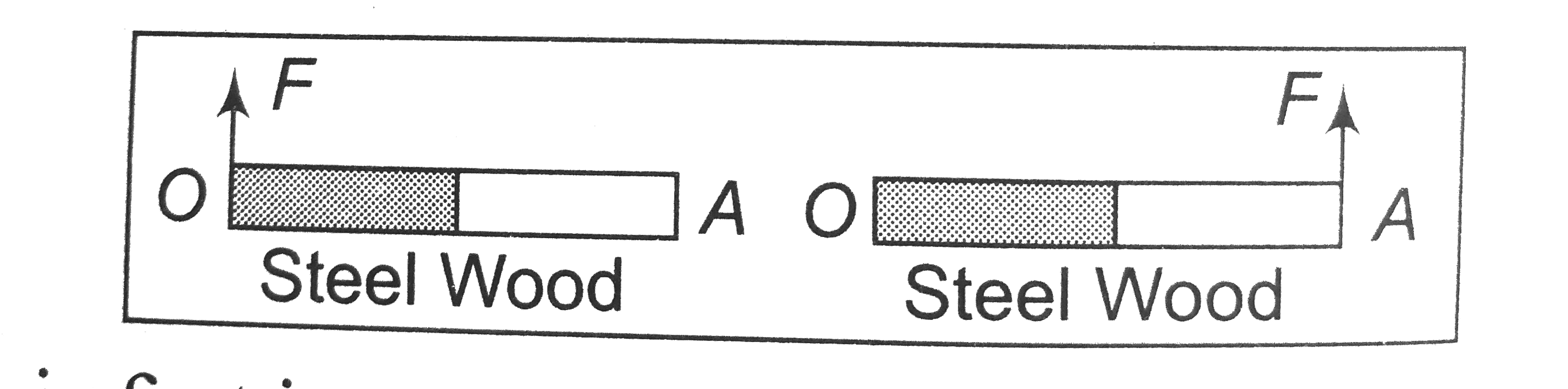 .
.
View SolutionWhen a rigid body is in motion, few particles of the body remain at rest at all times. What kind of motion is the rigid body having?
View SolutionIf a horizontal cylindrical tube, partly filled with water is rapidly rotated about a vertical axis passing through its centre, the moment of inertia of the water about its axis will
View SolutionA flywheel rotating about a fixed axis has a kinetic energy of 225 J when its angular speed is 30 rad/s. What is the moment of inertia of the flywheel about its axis of rotation?
View SolutionA whell of mass 4 kg and radius of gyration 0.4 m is making 300 r.p.m. Its moment of inertia is
View SolutionA flywheel rotating about a fixed axis has a kinetic energy of `360J` when its angular speed is `30` radian `s^(-1)` . The moment of inertia of the wheel about the axis of rotation is
View SolutionA circular disc of mass 2 kg and radius 0.1 m is rotating at an angular speed of 2 rad/s, about an axis passing through its centre and perpendicular to its plane. What is its rotational kinetic energy?
View SolutionThe K.E. of a body is 3 joule and its moment of inertia is `"6 kg m"^(2)`. Then its angular momentum will be
View SolutionA ring and a thin hollow cylinder have the same mass and radius. If `I_(r )` and `I_(s)` represent their moment of inertia about their axes, then
View SolutionWhen the speed of a flywheel is increased from 240 r.p.m. to 360 r.p.m., the energy spent is 1936 J.
What is te moment of inertia of the flywheel?
View SolutionA body having M.I of `5kg-m^(2)` about its axis of rotation is rotating with angular velocity of 6 rad/s. The kinetic energy of the rotating body is the same as that of a body of mass 5 kg moving with a speed of
View SolutionA solid disc is rotating at an angular speed of 20 rad/s. It is decelerated at a constant rate of `"2 rad/s"^(2)`. Through what angle the disc will turn before coming to rest?
View SolutionA wheel is rotating at 900 rpm about its axis. When the power is cut off, it comes to rest in 1 min. The angular retardation (in rad `s^(-2)`) is
View SolutionThe moment of an inertia about an axis of a body which is rotating with angular velocity `"1rad s"^(-1)` is numerically equal to
View SolutionA thin metal disc of mass 2 kg starts from rest and rolls down a smooth inclined plane. Its rotational K.E. is 4 J at the bottom of the inclined plane. What is its linear velocity at the same point?
View SolutionA body of moment of inertia about its axis of rotation is `3 kg m^(2)` and angular velocity 3 rad/s. The kinetic energy of rotating body is same as that of body of mass 27 kg moving with a speed of
View SolutionIn a rectangle `ABCD (BC=2AB)`. Along which axis the moment of inertia will be the minimum?
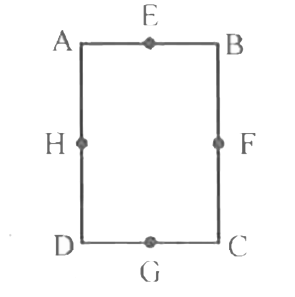
View SolutionOf the two eggs which have identical sizes, shapes and weights, one is raw and other is half boiled. The ratio between the moment of inertia of the raw to the half boiled egg about central axis is:
View SolutionWhen a disc rotates with uniform angular velocity, which of the following is not true ?
View SolutionA uniform square plate has a small piece `Q` of an irregular shape removed and guled to the centre of the plate leaving a hole behind in figure. The moment of inertia about the z-axis is then,
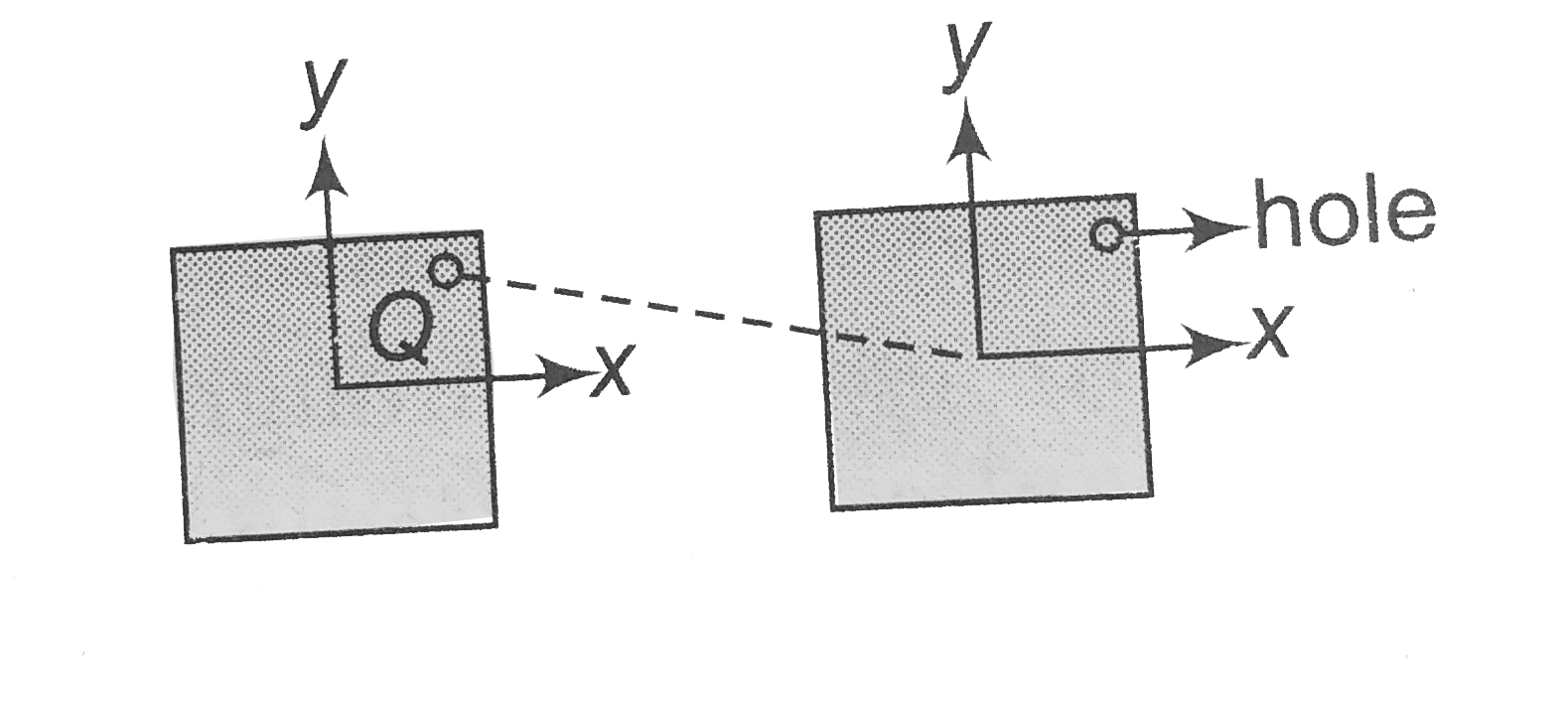 .
.
View SolutionA solid sphere of mass M and radius R spins about an axis passing through its centre making 600 r.p.m. What is its kinetic energy of rotation?
View SolutionThree mass points `m_(1), m_(2), m_(3)`are located at the vertices of an equilateral triangle of length a. What is the moment of 'inertia' of the system about an axis along an axis along the altitude of the triangle passing through `m_(1)`?
View SolutionA heavy body and a light body have equal K.E. which one of them has hreater momentum?
View SolutionIf the angular velocity of a body increases by `20%` then its kinetic energy of rotation will increase by
View SolutionThe angular velocity of a body is increased from 5 rad/s to 20 rad/s, without applying a torque but by changing its moment of Inertia. What is the relation between the new radius of gyration and the initial radius of gyration?
View SolutionA body rolls down a smooth inclined plane. If its rotational kinetic energy is `40%` of its translational K.E., then the body must be a
View SolutionTwo solid spheres of the same mass are of steel and aluminium. If `I_(S) and I_(A)` denote their moments of inertia about their diameters, then
View SolutionA uniform metre scale of mass 0.2 kg is rotated about an axis passing through its one end and perpendicular to its length, at the rate of 60 revolutions/minute. What is its kinetic energy of rotation? `("use "pi^(2)=10)`
View SolutionTwo loops P and Q are made from a uniform wire. The radii of P and Q are `R_(1) and R_(2)` respectively and their moments of inertia are `I_(P) and I_(Q)` respectively.
If `(I_(P))/(I_(Q))=8` then `(R_(1))/(R_(2))` is
View SolutionThe moment of inertia of a circular disc of mass `M` and radius `R` about an axis passing thrugh the center of mass is `I_(0)`. The moment of inertia of another circular disc of same mass and thickness but half the density about the same axis is
View SolutionA car is moving with a constant speed. The wheels of the car make 120 rotations per minute. The brakes are applied and the car comes to rest in 8 second. How many rotations are completed by the wheels, before the car is brought to rest? (Assume that the brakes produce a constant retarding force)
View SolutionThe ratio of the dimension of Planck's constant and that of moment of inertia is the dimension of
View SolutionTwo circular discs A and B have equal masses and equal thicknesses but have densities `d_(1) and d_(2)` such that `d_(1) gt d_(2)`. Their moments of inertia are related as
View SolutionA ody is in pure rotation. The linear speed v of a particle, the distance r of the particle from the axis and the angular velocity `omega` of the body are related as `omega=v/r`. Thus
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionFour point masses, each of value m, are placed at the corners of a square ABCD, having each side of length L. What is the moment of inertia of this system about an axis passing through A and parallel to the diagonal BD?
View SolutionIf `rho` is the density of its material, then its rotational K.E. is given by
View SolutionThe density of a rod AB increases linearly from A to B its midpoint is O and its centre of mass is at C. four axes pass through A, B, O and C, all perpendicular to the length of the rod. The moment of inertial of the rod about these axes are `I_(A), I_(B), I_(O)` and `I_(C)` respectively.
View SolutionThe diameter of a disc is increased by `2%` without changing its mass. What is the percentage increase in its moment of inertia about its axis of symmetry?
View SolutionA molecule consists of two atoms each of mass m and separated by a distance d. If K is the average rotational K.E. of the molecule at particular temperature, then its angular frequency is
View SolutionWhen a ceiling fan is switched off, its angular velocity reduces to 50% while it makes 36 rotations. How many more rotations will it make before coming to rest?(Assume uniform angular retardation)
View SolutionThree particles each of mass m gram are situated at the vertices of an equilateral triangle ABC of side L cm as shown in the figure.
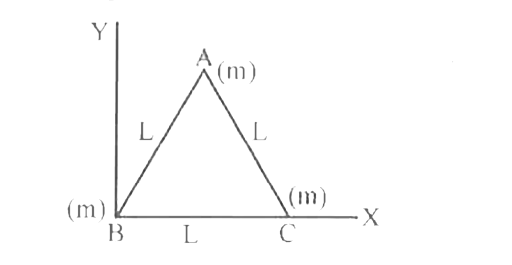
The moment of inertia of the system about a line BY perpendicular to BC and in the plane ABC is
View SolutionTwo discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity `2 omega` using the entire potential energy of a spring compressed by a distance `x_1` Disc B is imparted an angular velocity `omega` by a spring having the same spring constant and compressed by a distance `x_2` Both the discs rotate in the clockwise direction.
The ratio `x_1//x_2` is
View SolutionA hollow spere of mass M and radius R is rotating with angular frequency `omega` it suddenly stops rotating and 75% of kinetic energy is converted to heat if s is the speicific heat of the material in j / kg k then rise in temperature of the spere is (MI of hollow sphere `=2/3MR^(2)`
View SolutionA disc of moment of inertia `9.8//pi^(2)kg m^(2)` is rotating at 600 rpm. If the frequency of rotation changes from 600 rpm to 300 rpm, then what is the work done ?
View SolutionAn automobiles engine develops a power of 100 kilowatt, when rotating at a speed of 30 rev/sec. What torque does it deliver?
View SolutionThe fly wheel of a motor has a moment of inertia of 90 `kg-m^(2)`. If the motor produces a constant torque of 270 N-m, then the angular acceleration produced in the fly wheel.
View SolutionIf there a change in the angular momentum of a body from `"5 kg-m"^(2)//s` to `"8 kg-m"^(2)//s` in 4 seconds, then the torque acting on the body is
View SolutionA torque of magnitude 500 Nm acts on a body of mass 16 kg and produces and angular acceleration of `"20 rad/s"^(2)`. The radius of gyration of the body is
View SolutionA constant torque of 31.4 Nm is applied to a pivoted wheel. If the angular acceleration of the wheel is `2pi" rad/s"^(2)`, then its moment of inertia is
View SolutionUnder a constant torque, the angular momentum of a body changes from 2x to 5x in 8 sec. The torque acting on the body is
View SolutionA wheel has a moment of inertia of `5xx10^(-3) kg m"^(2)` and is making `"20 rev/s".` What is the magnitude of the torque required to stop it in 10 s?
View SolutionA wheel having moment of inertia `2 kg m^(2)` about its vertical axis, rotates at the rate of `60 rpm` about this axis. The torque which can stop the wheel's rotation in one minute would be
View SolutionA constant torque of `31.4 N-m` id exterted on a pivoted wheel. If the angular acceleration of the wheel is `4 pi rad//s^2`, then the moment of inertia will be.
View SolutionTorques of equal magnitude are applied to a thin hollow cylinder and a solid sphere, both having the same mass and radius. Both of them are free to rotate about their axis of symmetry. If `alpha_(c) and alpha_(s)` are the angular accelerations of the cylinder and the sphere respectively, then the ratio `(alpha_(c))/(alpha_(s))` will be
View SolutionA torque of 100 N-m acting on a wheel at rest, rotates it through 200 radian in 10 s. What is the moment of inertia of the wheel?
View SolutionA toraue of magnitude 4000 N-m, acts on a body of mass 2 kg. If the angular acceleration produced in the body is `"20 rad/s"^(2)`, then the radius of gyration of the body is
View SolutionA rope of negligible mass is wound around a hollow cylinder of mass 4 kg and radius 40 cm. What is the angular acceleration of the cylinder, if the rope is pulled with a force of 4N? Assume that there is no splipping.
View SolutionA force of `-Fhatk` acts on O, the origin of the coodinate system. The torque about the point (1,-1) is
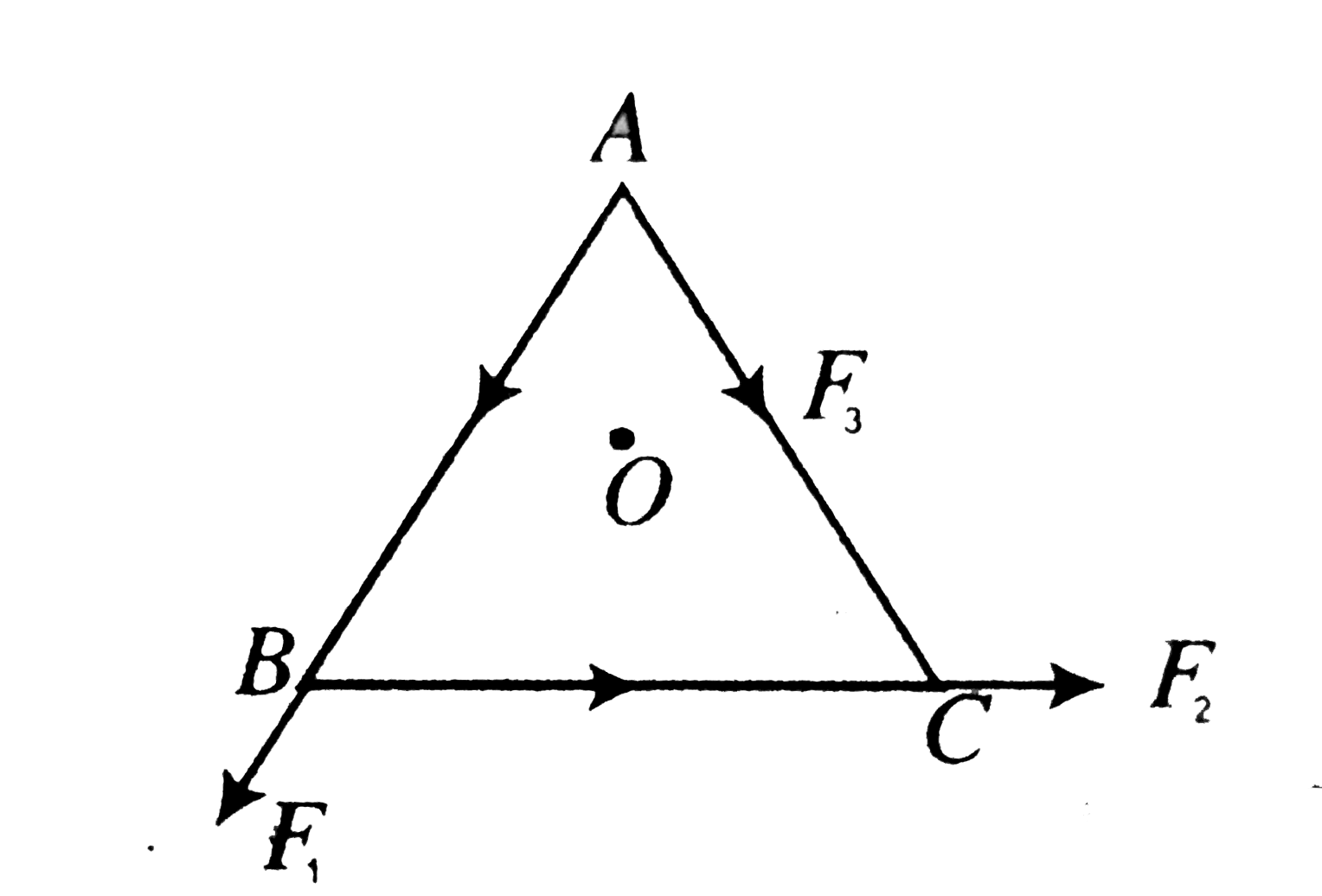
View Solution`O` is the centre of an equilateral triangle `ABC`. `F_(1), F_(2)` and `F_(3)` are the three forces acting along the sides `AB, BC` and `AC` respectively. What should be the value of `F_(3)` so that the total torque about `O` is zero?
View SolutionWhich one of the following relations is wrong?
View SolutionA toruque `tau` produces an angular acceleration in a body rotating about an axis of rotation. The moment of inertia of the body is increased by `50%` by redistributing the masses, about the axis of rotation. To maintain the same angular acceleration, the torque is changed to `tau'`. What is the relation between `tau and tau'`?
View SolutionA costant torque of 400 N turns a flywheel at rest and of `"M.I. 100 kgm"^(2)` about an axis through its centre. What is the change in its angular velocity in 4 s?
View SolutionWhat is the power of an engine, if it applies a toque of 180 Nm, to rotate a rotor at a uniform angular speed of 100 rad/s?
View SolutionA rope is wound round a hollow cylinder of mass 5 kg and radius 0.5m. What is the angular acceleration of the cylinder if the rope is pulled with a force of 20 Ngt
View SolutionThe angular velocity of a body is given by
`vec(omega)=3hati+2hatj+3hatk`
A torque `vec(tau)=2hati+3hatj+4hatk` acts on it. Then the rotational power will be
View SolutionA ring and a disc of different masses are rotating with the same kinetic energy. If a retarding torque `(tau)` is applied to the ring, the ring stops after completing n rotations. If the same retarding torque is applied to the disc, how many rotations would it complete before coming to rest?
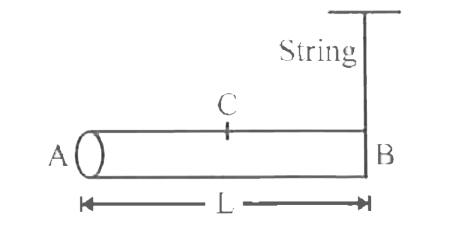
View SolutionA uniform rod AB of length L and and weight Mg is hinged at one end A. The rod is kept in the horizontal position by a massless string. If the string is cut, then the angular acceleration of the rod will be
`["M.I. of the rod about A is "(ML^(2))/(3)]`
View SolutionLet `vecF` be the force acting on a particle having position vector `vecr` and `vec(tau)` be the torque of this force about the origin. Then
View SolutionA rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be
View SolutionA wheel is at rest in the horizontal position. Its moment of inertia about a vertical axis passing through its centre is `"15 kgm"^(2)`. A constant torque of 300 N-m is now applied to it for 5 second. What is the change in its kinetic energy?
View SolutionA uniform disc of mass 500 kg and radius 2 metres is rotating at the rate of 600 rpm. What is the torque required to rotate the disc in the opposite direction with the same speed in a time of 100 seconds?
View SolutionA cord is wound round the circumference of wheel of radius `r`. The axis of the wheel is horizontal and fixed and moment of inertia about it is `I`. A weight `mg` is attached to the end of the cord and falls from rest. After falling through a distance `h`, the angular velocity of the wheel will be.
View SolutionA solid cylinder of mass `50 kg` and radius `0.5 m` is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other end hanging freely. Tension in the string required to produce an angular acceleration of `2` revolution `s^(-2)` is
View SolutionA torque of 75 Nm acts on a body at rest for 4 s. What is the change in its angular momentum?
View SolutionA ring of mass 10 kg and radius 0.2 m is rotating about its geometrical axis at 20 rev/sec. Its moment of inertia is
View SolutionA rod of length 2 m, has a mass of 0.12 kg. Its moment of inertia about an axis passing through its one end and perpendicular to the length of the rod is
View SolutionA uniform disc of mass 5 kg has a radius of 0.5 m. Its moment of inertia about an axis passing through a point on its circumference and perpendicular to its plane is
View SolutionA rod of length 2 m has a mass of 0.24 kg. Its moment of inerita about an axis passing through its centre and perpendicular to the length of the rod is
View SolutionA disc of mass 2 kg is rolling on a horizontal surface without slipping with a velocity of 0.1 m/s. What is its rotational kinetic energy?
View SolutionThe moment of inertia of a circular disc about an axis passing through its centre and normal to its plane is `"50 kg - m"^(2)`. Then its moment of inertia about a diameter is
View SolutionA solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
View SolutionTwo rings have their M.I. in the ratio 2:1. If their diameters are in the ratio of 2:1, then the ratio of their masses will be
View SolutionTwo circular discs are of same thickness. The diameter of `A` is twice that of `B`. The moment of inertia of `A` as compared to that of `B` is
View SolutionThe diameter of a thin circular disc of mass 2 kg is 0.2 m. Its moment of inertia about an axis passing through the edge and perpendicular to the plane of the disc is
View SolutionThe radius of gyration of a disc of mass 100 g and radius 5 cm about an axis passing through its centre of gravity and perpendicular to the plane is
View SolutionThe moment of inertia of a ring of mass 5 gram and radius 1 cm about and axis passing through its edge and parallel to its natural axis is
View SolutionThe M.I. of a ring about an axis passing through its centre and perpendicular to its plane is `"2 kg - m"^(2)`, then its M.I. about any diameter is
View SolutionM.I. of a thin uniform rod about the axis passing through its centre and perpendicular to its length is `ML^(2)//12` . The rod is cut transversely into two halves, which are then riveted end to end.M.I. of the composite rod about the axis passing through its centre and perpendicular to its length will be
View Solution
MULTIPLE CHOICE QUESTION questions and complete solutions for chapter ROTATIONAL MOTION of MARVEL PHYSICS (HINGLISH) of Class 12