Complete Solutions to MULTIPLE CHOICE QUESTIONS of chapter KINETIC THEORY OF GASES ,THERMODYNAMICS AND RADIATION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | KINETIC THEORY OF GASES ,THERMODYNAMICS AND RADIATION |
| MARVEL | MULTIPLE CHOICE QUESTIONS |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A vessel contains 60,000 molecules of a gas. Due to a very fine hole in the wall, 10,000 molecules escape from the vessel. Then the mean free path of the molecules of the gas
View SolutionThere are N molecules of a gas in a containter. If this number is increased to 2N, what will be (i) pressure (ii) total energy (iii) rms speed of the gas ?
View SolutionAt constant volume, temperature is increased. Then
View SolutionFor a planet, the escape velocity is `V_(e)`. The presence of atmosphere on the planet shows that the
View SolutionThe root mean square velocity of the molecules of a gas is `200m//s`. What will be the rms velocity of the molecules if the atomic weight is doubled and the absolute temperature is halved?
View SolutionMolecular weight of oxygen is 32 and that of hydrogen is 2. The ratio of the rms velocity of hydrogen molecule at 400K to rms velocity of oxygen molecule at 900 K is given by
View SolutionThe absolute temperature of the gas is increased 3 times. What will be the increases in root mean square velocity of the gas molecules?
View SolutionThe temperature of the gas is raised from `27^(@)C` to `927^(@)C`, the root mean square velocity is
View SolutionThe velocities of 5 molecules are `2m//s,3m//s,4m//s,5m//s and 6m//s` respectively. What is their mean velocity?
View SolutionThe velocities of 4 molecules are `2m//s, 4m//s, 5m//s and 6m//s` respectively. What is their mean square velocity?
View SolutionThe translational K.E. of the molecules of a gas at absolute temperature (T) can be doubled
View SolutionThe root mean square speed of hydrogen molecule at 300 K is 1930m/s. Then the root mean square speed of oxygen molecules at 900K will be………..
View SolutionA vessel contains one mole of oxygen and one mole of hydrogen at N.T.P. What is the ratio of the values of rms velocities of hydrogen and oxygen molecules?
View SolutionThe rms speed of the molecules of a gas in a vessel at `80^(@)C` is `200m//s`. If 40% of the gas is taken out of the vessel, what is the rms speed of the remaining molecules if their temperature is not changed?
View SolutionThe mean free path of a gas molecule at `27^(@)C` is 2 cm. If the rms velocity of the gas at that temperature is `10m//s`, what is the time interval between two successive collisions?
View SolutionWhich of the following gases has maximum rms speed at a given temperature?
View SolutionThe phenomenon of Brownian motion is taken as an evidence of
View SolutionThe molecules of an ideal gas possesses
View SolutionThe number of molecules in a gram-mole of molecule of a gas is called
View SolutionWhen a gas is compressed as constant temperature:
View SolutionThe temperature of the gas is raised from `27^(@)C` to `927^(@)C`, the root mean square velocity is
View SolutionAt a certain temperature, hydrogen molecules have r.m.s. velocity of `3km//s`. What is the r.m.s. velocity of the oxygen molecules at the same temperature ?
View SolutionAt what temperature, the r.m.s. speed of the molecules of a gas is half its value at NTP?
View SolutionThe r.m.s. velocity of the molecules of an ideal gas is C at a temperature of 100 K. At what temperature its r.m.s. velocity will be doubled ?
View SolutionThe temperature of a gas is - `68^(@)C`. To what temperature should it be heated, so that the r.m.s. velocity of the molecules be doubled ?
View SolutionThe velocities of 4 molecules are 4m/s, 5m/s, 6m/s and 2m/s respectively. What is their rms velocity?
View SolutionThe molecular weights of `H_(2) and O_(2)` are 2 and 32 respectively. The rms velocity of `H_(2)` molecule at N.T.P. is `2000m//s`. What is the rms velocity of Oxygen molecules at N.T.P. ?
View SolutionA sample of gas is at `0^(@)C`. The temperature at which its rms speed of the molecule will be doubled is
View SolutionIf the absolute temperature of a gas is increased 5 times, the r.m.s. velocity of the molecules will be
View SolutionRoot mean square velocity of gas molecules is `300 m//sec`. The `r.m.s` velocity of molecules of gas with twice the molecular weight and half the absolute temperature is :
View SolutionThe temperature of an ideal gas is increased from `27^(@)C` to `327^(@)C`. If the r.m.s. speed of its molecules at `27^(@)C` is `200m//s`, then the new r.m.s. speed at `600^(@)K` will be
View SolutionThe root mean square velocity of the molecules of a gas is `200m//s`. What will be the rms velocity of the molecules if the atomic weight is doubled and the absolute temperature is halved?
View SolutionFind the wrong statement from the following :
According to kinetic theory 0 K is that temperature at which
View SolutionThere is no atomosphere on moon because
View SolutionIn the equation `PV = nRT`, the value of 'R' will not depend on:
View SolutionThe rms speed of the molecules of a gas in a vessel is `400ms^(-1)`. If half of the gas leaks out at constant temperature, the rms speed of the ramaining molecules will be…………..
View SolutionAt what temperature will the r.m.s. speed of the hydrogen molecules be half of its value at `327^(@)C` ?
View SolutionThe velocity of 4 gas molecules are given by 1km/s , 3km/s , 5 km/s and 7km/s . Calculate the difference between average and RMS velocity .
View SolutionA gas is compressed isothermally . The rms velocity of its molecules
View SolutionThe temperature at which the rms velocity of oxygen molecules equals to that of nitrogen molecules at `0^(@)C` is
View SolutionA perfect gas of volume 10 litre is compressed isothermally to a volume of 1 litre, the rms speed of the molecules will
View SolutionA vessel X contains 1 mole of `O_(2)` gas (molar mass 32) at a temperature T and pressure p. Another ideantical vessel Y contains one mole of Ge gas (molar mass 4) at temperature 2T, then
View SolutionCooking gas container are kept in a lorry moving with uniform speed. The temperature of the gas molecules inside will
View SolutionAt what temperature is the rms velocity of a hydrogen molecule equal to that of an oxygen molecule at `47^(@)C`?
View SolutionIf `c_(s)` is the velocity of sound in air and c is rms velocity , then
View SolutionThe mean free path of molecules of a gas (radius r) is inversely proportional to
View SolutionRoot mean square velocity of a particle is v at pressure P. If pressure is increased two times, then the r.m.s. velocity becomes
View SolutionThe dimensions of universal gas constant is
View SolutionAir in a cylinder is suddenly compressed by a piston, which is then maintained at the same position. With the passage of time
View SolutionWhat will be the r.m.s. speed of a gas at `800^(@)K` ?
View SolutionThe temperature of a ideal gas is increased for 100 k to 400k. If at 100 K the root mea square velocity of the gas molecules is v, at 400K it becomes
View SolutionThe rms velocity of a gas kept at a temperature of `27^(@)C` in a vessel is `61m//s`. The vessel is filled with
[R = 8.31`J//mol K`]
View SolutionAt room temperature the rms speed of the molecules of a certain diatomic gas is formed to be `1930m//sec` The gas is .
View SolutionIf we travel from the troposphere to the thermosphere, the mean free path of the ait molecules
View SolutionThe speed of sound in oxygen `(O_2)` at a certain temperature is `460ms^-1`. The speed of sound in helium (He) at the same temperature will be (assume both gases to be ideal)
View SolutionThree closed vessels `A, B` and `C` are at the same temperature T and contain gases which obey the Maxwellian distribution of velocities. Vessel A contains only `O_(2), B` only `N_(2)` and `C` a mixture of equal quantities of `O_(2)` and `N_(2)`. If the average speed of the `O_(2)` molecules in vessel `A` is `V_(1)`, that of the `N_(2)` molecules in vessel `B` is `V_(2)`, the average speed of the `O_(2)` molecules in vessel `C` is (where `M` is the mass of an oxygen molecules)
View SolutionTwo identical containers A and B with frictionless pistons contain the same ideal gas at the same temperature and the same velocity V. The mass of the gas in A is `m_A,` and that in B is `m_B`. The gas in each cylinder is now allowed to expand isothermally to the same final volume 2V. The changes in the pressure in A and B are found to be `DeltaP and 1.5 DeltaP` respectively. Then
View Solution1 mole of `H_(2)` gas in contained in a box of volume V 1.00 `m^(3)` at T =300 K. The gas is heated to a temperature of T= 3000K and the gas gets converted to a gas of hydrogen atoms. The final pressure would be (considering all gases to be ideal)
View SolutionWhat is the density of a gas at N.T.P. if the rms velocity of the gas molecules is `400m//s`? (Take atmospheric pressure `P = 1xx10^(5)N//m^(2)`)
View Solutionn balls each of mass m impinge elastically each second on a surface with velocity u. The average force experienced by the surface will be
View Solutionn balls each of mass m impinge elastically each second on a surface with velocity u. The average force experienced by the surface will be
View SolutionA molecule of mass m moving with a velocity v makes 5 elastic collisions with a wall of the container per second. The change in its momentum per second will be
View SolutionThe root mean square speed of the molecules of an enclosed gas is 'v'. What will be the root mean square speed if the pressure is doubled, the temperature remaining the same?
View SolutionEqual volumes of two gases, having their densities in the ratio `1 : 16` exert equal pressures on the walls of two containers. The ratio of their rms velocities `(C_(1)/C_(2))` is
View SolutionIf the pressures exerted by two ideal gases are in the ratio `3 : 2` and their densities are in the ratio `2 : 1`, then the ratio of their r.m.s. velocities is
View SolutionAt a constant temperature, what is the relation between pressure P and density `rho` of gas?
View SolutionGases excert pressure on the walls of the container , because the gas molecules
View SolutionIf masses of all molecules of a gas are halved and the speed doubled. Then the ratio of initial and final pressure is :
View SolutionGas at a pressure `P_(0)` in contained as a vessel. If the masses of all the molecules are halved and their speeds are doubles. The resulting pressure P will be equal to
View SolutionConsider a gas with density `'rho'` and `overlinec` as the root mean square velocity of its molecules contained in a volume. If the system moves as whole with velocity 'v' , then the pressure exerted by the gas is
View Solution`10^(23)` molecules of a gas, each having a mass of `3xx10^(-27)` kg strike per second per sq. cm. of a rigid will at an angle of `60^(@)` with the normal and rebound with a velocity of `500m//s`. What is the pressure exerted by the gas molecules on the wall?
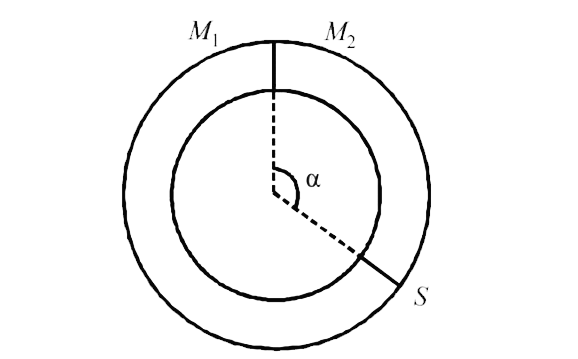
View SolutionA ring shaped tube contain two ideal gases with equal masses and relative molar masses `M_1=32 and M_2=28.`
The gases are separated by one fixed partiotin and another movable stopper S which can move freely without friction inside the ring. The angle `alpha` as shown in the figure is ...... degrees.
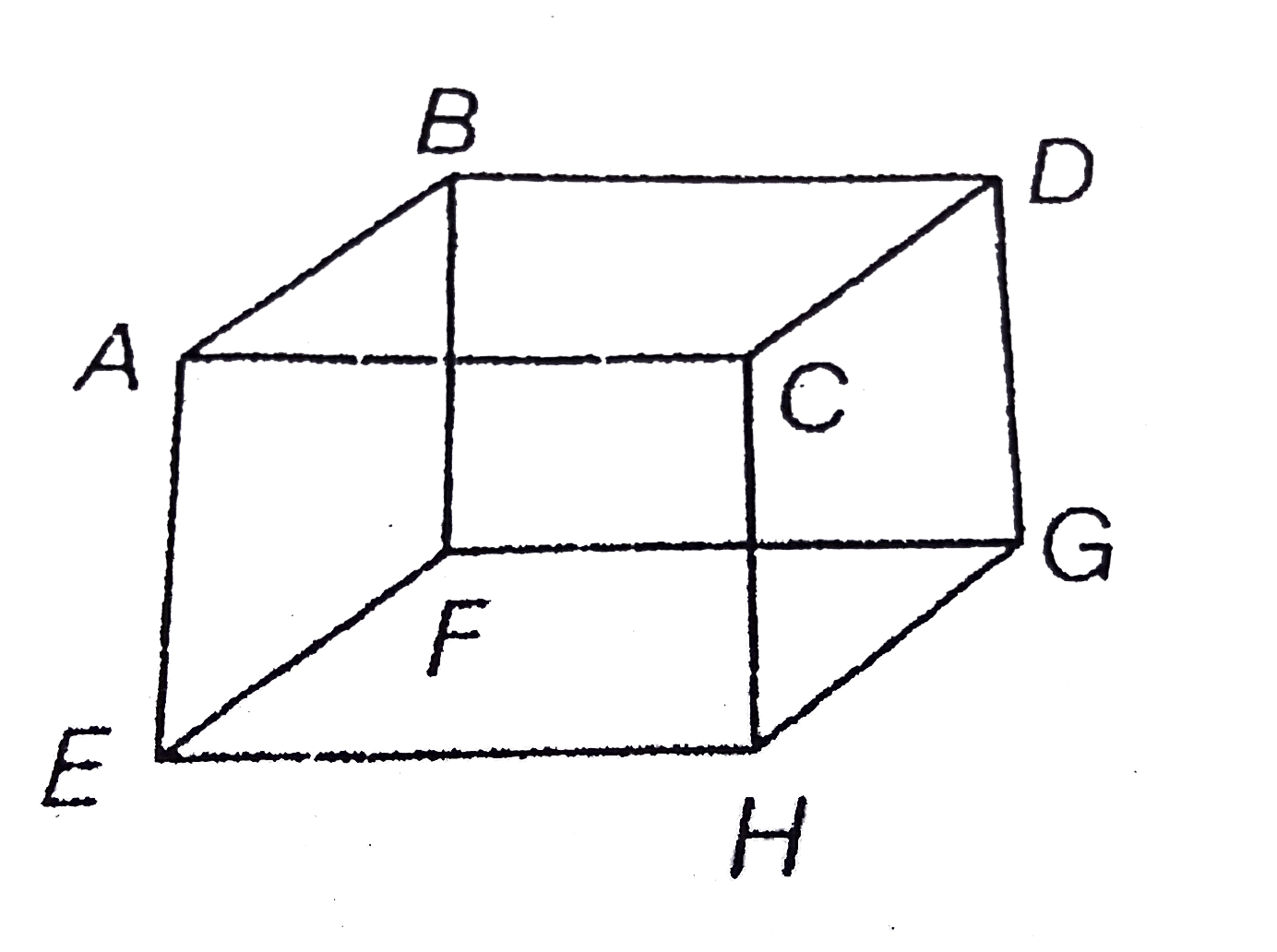
View SolutionMole of an ideal gas is contained in a cubical volume V, ABCDEFGH at 300 K (figure). One face of the cube (EFGH) is made up of a material which totally absorbs any gas molecule incident on it .At any given time.
View SolutionAt the same temperature, the mean kinetic energies of the molecules of hydrogen and oxygen are in the ratio
View SolutionThe kinetic energy per cubic metre of a perfect gas at N.T.P. is (Take atmospheric pressure `=1xx10^(5)N//m^(2)`)
View SolutionThe kinetic energy of one gram molecule of a gas at normal temperature and pressure is `(R=8.31J//mol-K)`
View SolutionIn case of Boyle's law, if the pressure is increased by 1% the percentage decrease in volume is
View SolutionIf the universal gas constant is `8.3J//"mole"//K` and the Avogadro's number is `6xx10^(23)`, then the mean K.E. of the oxygen molecules at `327^(@)C` will be
View SolutionThe kinetic energy of a gas at `27^(@)C` is E. What will be its K.E., if the temperature is increased to 500 K ?
View SolutionA monoatomic gas of n -moles is heated from temperature T to T under two different conditions (i) at constant volume and (ii) at constant pressure. The change in internal energy of the gas is
View SolutionThe average kinetic energy of the molecules of a gas at `27^(@)` is `9xx10^(-20)J`. What is its average K.E. at `227^(@)C` ?
View SolutionIf the pressure of an ideal gas is decreased by 10% isothermally, then its volume will
View SolutionIf E is the kinetic energy per mole of a gas, and T is the absolute temperature, then the universal gas constant is given by
View SolutionA gas has volume V and pressure P. The total translational kinetic energy of all the molecules of the gas is equal to `3/2PV`
View SolutionAt what temperature will the average K.E. of the hydrogen molecules be half of its value at N.T.P. ?
View SolutionIn the Boyle's law experiment, if the volume of the enclosed air is to be decreased from 20 cc to 18 cc, then its pressure should be increased by about
View SolutionIn the expression for boyle 's law the product pV has dimensions of
View SolutionKE per unit volume is E. The pressure exerted by the gas is given by
View SolutionThe kinetic energy of translation of 20gm of oxygen at `47^(@)C` is (molecular wt. of oxygen is 32 gm/mol and R=8.3 J/mol/K)
View SolutionThe average translational K.E. of `O_(2)` molecules (Molecular weight = 32) at a particular temperature is 0.035 eV. What is the average translational K.E. of `N_(2)` molecules (Molecular weight = 28) at the same temperature ?
View SolutionThe average translational K.E. of the molecules in a sample of oxygen at 300K is `6xx10^(-20)J`. What is the average translational energy at 750 K?
View SolutionHow much should the pressure be increased in order to decrease the volume of a gas 5% at a constant temprature ?
View SolutionThe average translational energy and the rms speed of molecules in a sample of oxygen gas at `300K` are `6.21xx10^(-21)J` and `484m//s`, respectively. The corresponding values at `600K` are nearly (assuming ideal gas behaviour)
View SolutionA mixture of 2 moles of helium gas (`(atomic mass)=4a.m.u`) and 1 mole of argon gas (`(atomic mass)=40a.m.u`) is kept at 300K in a container. The ratio of the rms speeds `((v_(rms)(helium))/((v_(rms)(argon))` is
View SolutionTwo thermally insulated vessel 1 and 2 are filled with air at temperature `(T_1T_2), volume (V_1V_2)` and pressure `(P_1P_2)` respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
View SolutionAt what temperature does the average translational K.E. of a molecule in a gas becomes equal to K.E. of an electron accelerated from rest through potential difference of V volt ? All symbols have their usual meaning.
View Solution`T_(1)` is the temperature of oxygen enclosed in a cylinder. The temperature is increased to `T_(2)` and Maxwellian distribution curves for `O_(2)` at temperatures `T_(1) and T_(2)` are plotted. If `A_(1) and A_(2)` are the areas under the curves and the speed axis, in both cases, then
View SolutionCalculate the total number of degree of freedom for a mole of diatomic gas at STP.
View SolutionThe value of `gamma=C_(P)/C_(V)` for a gas is given by `gamma=1+2/f` where f is the number of degrees of freedom of a molecule of a gas
What is the ratio of `(gamma_("monoatomic"))/(gamma_("diatomic"))` ?
View SolutionThe gases carbon-monoxide (CO) and nitrogen at the same temperature have kinetic energies `E_(1)` and `E_(2)` respectively. Then
View Solution
MULTIPLE CHOICE QUESTIONS questions and complete solutions for chapter KINETIC THEORY OF GASES ,THERMODYNAMICS AND RADIATION of MARVEL PHYSICS (HINGLISH) of Class 12