Complete Solutions to EXAMPLE of chapter INTEGRALS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | INTEGRALS |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Integrate the following.
`intsinxsin2xsin3xdx`
View SolutionIntegrate the following.
`intsec^2xcos^(2)2xdx`
View SolutionFind `intfrac(2+sin2x)(1+cos2x)e^xdx`
View SolutionEvaluate `intfrac(sec^2xdx)(sqrt(tan^2x+4))`
View SolutionFind the following integrals.
`int_0^(pi/2)frac(sinx)(1+cos^2x)dx`
View SolutionFind the following integrals.
`int_0^1xe^(x^2)dx`
View SolutionFind the following integrals.
`int_0^(pi/2)sqrtsinxcos^5xdx`
View SolutionFind the following integrals.
`int_0^2xsqrt(x+2)dx`
View SolutionFind the following integrals.
`int_0^(pi/2)sqrtsinxcosxdx`
View SolutionFind the following integrals.
`int_0^(pi/2)frac(1)(4sin^2x+5cos^2x)dx`
View SolutionIf `f(x)` is an odd function,then `int_-a^af(x)=?`
View SolutionEvaluate
`int_(-pi/2)^(pi/2)sin^99x*cos^100xdx`
View SolutionEvaluate
`int_-1^1e^absxdx`
View SolutionShow that `cos^2x` is an even function.
View SolutionEvaluate `int_(-pi/4)^(pi/4)cos^2xdx`
View SolutionFind the following integrals.
`intfrac(1)(9x^2+6x+5)dx`
View SolutionFind the following integrals.
`intfrac(1)(sqrt(7-6x-x^2))dx`
View SolutionFind the following integrals.
`int_0^(pi/2)frac(sqrtsinx)(sqrtsinx+sqrtcosx)dx`
View SolutionFind the following integrals.
`int_0^(pi/2)frac(sin^5x)(sin^5x+cos^5x)dx`
View SolutionFind the following integrals.
`int_0^2xsqrt(2-x)dx`
View SolutionFind the following integrals.
`int_2^8abs[x-5]dx`
View SolutionFind the following integrals.
`int_-5^5abs[x+2]dx`
View SolutionFind the following integrals.
`intfrac(1)(3+cosx)dx`
View SolutionFind the following integrals.
`intfrac(2x)(x^2+3x+2)dx`
View SolutionFind the following integrals.
`intfrac(x^2+x+1)((x+2)(x^2+1))dx`
View SolutionFind the following integrals.
`intfrac(1)((x+1)^2-4)dx`
View SolutionFind the following integrals.
`intfrac(1)(x(x^3+1))dx`
View SolutionFind the following integrals.
`inte^(2x)sin3xdx`
View SolutionFind the following integrals.
`intxsin^-1xdx`
View Solutionwhich of the following is the value of
`intfrac(dx)(sqrt(a^2-x^2))`
View SolutionEvaluate `intfrac(2x)(x^2+3x+2)dx`
View SolutionChoose the correct answer from the
bracket.
`inte^xdx`=----`(e^(2x)+c,e^x+c,e^-x+c,e^(-2x)+c)`
View SolutionEvaluate `inte^xsinxdx`
View Solution`f(x)intg(x)dx-int(f'(x)intg(x)dx)dx`
View SolutionIntegrate `sin^-1sqrtfrac(x)(a+x)`w.r.to x.
View SolutionMatch the following.
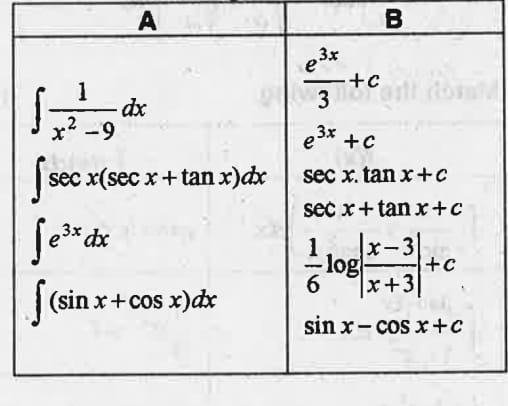
View SolutionEvaluate `intfrac(x)(sqrt(x+a)+sqrt(x+b))dx`
View SolutionMatch the following.
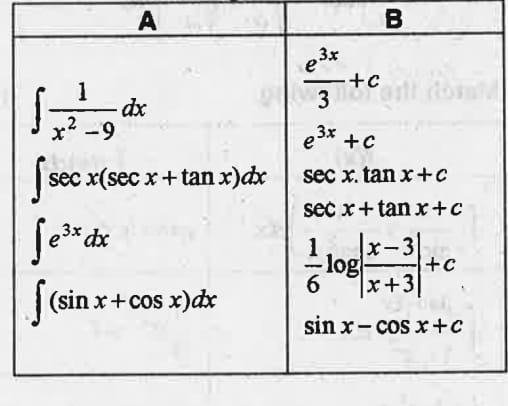
View SolutionConsider the integral I=`intfrac(xsin^-1x)(sqrt(1-x^2))dx`
what substitution can be given for simplifying
the above integral
View SolutionEvaluate the integral I=`intfrac(xsin^-1x)(sqrt(1-x^2))dx`
View SolutionConsider the integral I=`intfrac(xsin^-1x)(sqrt(1-x^2))dx` Evaluate I.
View SolutionEvaluate `int_0^(pi/2) log(tanx)dx`
View SolutionFind the following integrals.
`intfrac(sec^2x)(cosec^2x)dx`
View SolutionFind the following integrals
`intfrac(1)(x^2-6x+13)dx`
View SolutionMatch the following.Justify your answer
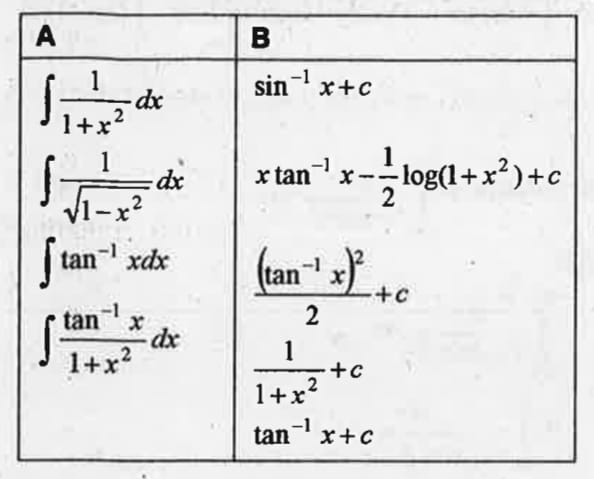
View Solution`intsin2xdx` =
View Solution(i)Resolve`frac(x^2+1)(x^2-5x+6)`into partial
fractions.
(ii)Hence evaluate `intfrac(x^2+1)(x^2-5x+6)`
View SolutionEvaluate.`int_0^4xdx` as a limit of sum
View SolutionDefine the real valued function
`f(x)=abs[x^2+2x-3`
View SolutionEvaluate `int_0^2abs[x^2+2x-3]dx`
View SolutionConsider the function `f(x)=absx+abs[x+1]`
define trhe function `f(x) in the interval
[-2,1]
View SolutionConsider the function `f(x)=absx+abs[x+1]`
Find the integral `int_-2^1f(x)dx`
View SolutionEvaluate `int_(pi/6)^(pi/3)frac(dx)(1+sqrttanx)dx`
View SolutionFill in the blanks.
`inttanxdx`=---
View SolutionFill in the blanks
`intcosxdx`=---
View SolutionFill in the blanks
`intfrac(1)(x)dx`=---
View SolutionEvaluate `intsin^3xcos^2xdx`
View SolutionFind the following integrals.
`int(3x-2)sqrt(x^2+x+1)dx`
View SolutionFind the following integrals.
`intfrac(2x-3)(x^2+3x-18)dx`
View SolutionFind the following integrals.
`intfrac(5x+2)(1+2x+3x^2)dx`
View SolutionFind the following integral.
` intfr(5x+3)/(sqrt(x^2+4x+10))dx`
View SolutionConsider the expression `frac(1)(x^3-1)`
Split it into partial fraction.
View SolutionConsider the expression `frac(1)(x^3-1)`
Split it into partial fraction.
View SolutionMatch the following

View Solutionconsider the function `f(x)=frac(x^4)(x+1)`
Evaluate `intf(x)dx`
View Solution(i)Evaluate the `int_0^2x^2dx` as the limit of a
sum.
(ii) Hence evaluate `int_-2^2x^2dx`
View SolutionFind `intsqrttanx dx`
View SolutionMatch the following
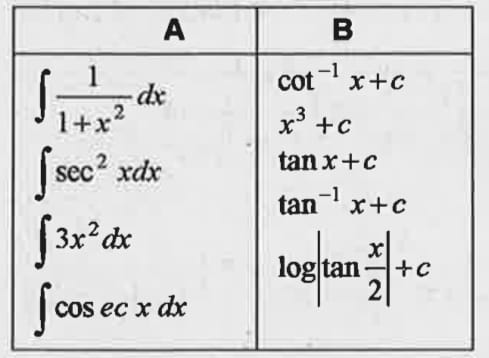
View SolutionIntegrate `frac(sec^2x)(5tan^2x-12tanx+4)`
View SolutionEvaluate `int_0^1sqrtxdx`
View Solution(i)If`int_0^asqrtxdx=2aint_0^(pi/2)sin^3xdx`,find the value of a.
(ii)Hence find `int_a^(a+1)xdx`
View SolutionLet `f(x)` be a function,then `int_0^af(x)dx`=?
View SolutionEvaluate
`int_0^2frac(sqrtx)(sqrtx+sqrt(2-x))dx`
View Solution`int_0^(pi/2)frac(sinx)(sinx+cosx)dx`
View SolutionFind the following integrals
`intfrac(2e^x)(e^(3x)-6e^(2x)+11e^x-6`
View SolutionFind the following integrals
`intfrac((3sinx-2)cosx)(5-cos^2x-4sinx)dx`
View SolutionFind `intfrac(1)(x^2+a^2)dx`
View Solutionshow that `3x+1=3/4(4x-2)+5/2`
View SolutionEvaluate `intfrac(3x+1)(2x^2-2x+3)dx`
View SolutionFind the Following integrals.
`intx^2e^(2x)dx`
View SolutionFind the Following integrals.
`inte^xsinxdx`
View Solution`inte^xsecx(1+tanx)dx=......`
View SolutionFind `intsin2xcos3xdx`
View SolutionFind the following integrals.
`int1/((x+1)(x+2))dx`
View SolutionFind the following integrals.
`int(2x-1)/((x-1)(x+2)^2)dx`
View SolutionConsider the integral `I=int_0^pi(xsinx)/(1+cos^2x)dx`
Express `I=pi/2int_0^pisinx/(1+cos^2x)dx`
View SolutionConsider the integral `I=int_0^pi(xsinx)/(1+cos^2x)dx`
Show that `I=pi^2/4`
View SolutionEvaluate: `int_2^3x/(x^2+1)dx`
View SolutionEvaluate:`int_0^pix/(1+sinx)dx`
View SolutionFind `int_0^1(2x+3)dx` as the limit of a sum.
View SolutionEvaluate`int_0^pilog(1+cosx)dx`
View SolutionFind `int_0^5(x+1)dx` as limit of a sum.
View SolutionEvaluate`int_0^4x^2dx` as the limit of a sum.
View SolutionFill in the blanks`int1/xdx=---`
View SolutionEvaluate `int(5x+1)/(x^2-2x-35)dx`
View SolutionIntegrate with respect to x.`sqrt(x^2+4x+8)`
View SolutionEvaluate `int-(cosec^2x)/sqrt(cot^2x+9)dx`
View SolutionEvaluate `int(cos^-1x)^2dx`
View SolutionEvaluate `int_0^pi (xsinx)/(1+cos^2x)dx`
View SolutionEvaluate `int_0^2e^xdx` as limit of a sum.
View Solution
EXAMPLE questions and complete solutions for chapter INTEGRALS of MAXIMUM PUBLICATION of Class 12