Complete Solutions to EXAMPLE of chapter VECTOR ALGEBRA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | VECTOR ALGEBRA |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Find `veca+vecb,veca-vecb` and `vecb+vecc` using the vectors.
`veca=3i+4j+k,vecb=2i-7j-3k` and `vecc=2i+3j-9k`.
View SolutionFind the vectors passing through the point `A(1,2,-3)` and `B(-1,-2,1)`.
View SolutionFind the Direction cosiness along `vec(AB)` where A(4,5,6) and B(6,3,8)
View SolutionShow that the points A, B and C with position vectors `veca=3i-4j-4k,vecb=2i-j+k` and `vecc=i-3j-5k` respectively form the vertices of a right angled triangle.
View SolutionProve that `[ veca+vecb vecb+vecc vecc+veca]=2[veca vecb vecc]`
View SolutionConsider the vector `vecp=2i-j+k`. Find two vectors `vecq` and `vecr` such that `vecp,vecq` and `vecr` are mutually perpendicular.
View SolutionFind `veca.vecb,vecatimesvecb` and `vecbtimesvecc` using the vectors.
`veca=3i+4j+k, vecb=2i-7j-3k` and `vecc=2i+3j-9k`.
View SolutionIf `veca=3i+j+2k,
`FInd` ` ` `magnitude` ` ` `of` ` ```vec a``
View SolutionIf `veca=3i+j+2k,`
If the projection of `veca` on another vector `vecb` is `sqrt14`, which among the following could be `vecb` ?
i+j+k
6i+2j+4k
3i-j+2k
2i+3j+k
View SolutionIf `veca=3i+j+2k`,
If `veca` makes an angle `60°` with a vector `vecc`, find the projection of `veca` on `vecc`.
View SolutionThe projection of the vector `2i+3j+2k` on the vector `i+j+k` is a)`frac(3)(sqrt3)` b)`frac(7)(sqrt3)` c)`frac(3)(sqrt17)` d)`frac(7)(sqrt17)`
View SolutionFind the area of a parallelogram whose adjacent sides are the vector `2i+j+k` and `i-j`.
View SolutionThe angle between the vectors `i+j` and `j+k` is
View SolutionIf `veca, vecb, vecc` are unit vectors such that
`veca+vecb+vecc=0`, find the value of
`veca.vecb+vecb.vecc+vecc.veca`.
View SolutionIf `veca, vecb, vecc` are unit vectors then,
`veca.veca`=_____
View SolutionHence, show that `veca.vecb+vecb.vecc+vecc.veca=(-3)/2` if `veca+vecb+vecc=0`.
View SolutionLet `A(2,3),B(1,4),C(0,-2)` and `D(x,y)` are vertices of a parallelogram ABCD.
Write the postion vectors A,B,C and D.
View SolutionLet `A(2,3),B(1,4),C(0,-2)` and `D(x,y)` are vertices of a parallelogram ABCD.
Find the value of x and y.
View SolutionFind the position vector of a point R which divides the line joining the points P and Q whose vectors are `i+2j-k` and `-i+j+k` in the ratio `2:1`
Internally.
View SolutionFind the position vector of a point R which divides the line joining the points P and Q whose vectors `i+2j-k` and `-i+j+k` in the ratio `2:1`
externally.
View SolutionChoose the correct answer from the backet. If a unit vector `hata` makes angles `pi/4` with i and `pi/3` with j and acute angle `theta` with k.
then `theta` is
View SolutionFind a unit vector `hata`.
View SolutionWrite down a unit vector in XY plane, making an angle of `60°` with the positive direction of x-axis.
View SolutionLet the vectors `veca,vecb,vecc` denotes the sides of a triangle ABC.
Prove that `vecatimesvecb=vecbtimesvecc=vecctimesveca`.
View SolutionFind the projection of a vector `i+3j+7k` on the vector `7i-j+8k`.
View SolutionIf `veca` and `vecb` are any two vectors, then `vecatimesvecb` is
a) a vector on the same plane where `veca` and `vecb` lie.
b) ab cos theeta
c) a vector parallel to both a and b
d) a vector perpendicular to both a and b.
View SolutionLet `veca=2i+4j-5k`, `vecb=i+2j+3k`. Then find a unit vector perpendicular to both `veca` and `vecb` .
View SolutionFind a vector of magnitude 5 in the direction parpendicular to both `veca` and `vecb` .
View SolutionConsider a vector that is inclined at an angle `45°` to x -axis and `60°` to y - axis. Find the dc's of the Vector.
View SolutionConsider a vector that is inclined at an angle `45°` to x -axis and `60°` to y - axis. Find a unit vector in the direction of the above vector.
View SolutionFind a vector which is of magnitude 10 units in the direction of the above vector.
View SolutionConsider the point `A(2,1,1)` and `B(4,2,3)`
Find the vector `vec(ab)`
View SolutionConsider the point `A(2,1,1)` and `B(4,2,3)`.Find the direction cosines of `vec(ab)`
View SolutionConsider the point `A(2,1,1)` and `B(4,2,3)`. Find the angle made by `vec(ab)` with the positive direction of X-axis.
View SolutionIf `i+j+k,2i+5j,3i+2j-3k,i-6j-k` respectively are the position vector of points A,B,C and D. Then find `vec(AB)` and `vec(CD)`.
View SolutionIf `i+j+k,2i+5j,3i+2j-3k,i-6j-k` respectively are the position vector of points A,B,C and D. Then find the angle between the vectors `vec(AB)` and `vec(CD)`.
View SolutionIf `i+j+k,2i+5j,3i+2j-3k,i-6j-k` respectively are the position vector of points A,B,C and D. Then
Deduce that `vec(AB)` parallel to `vec(CD)`.
View SolutionLet ABCD be a parallelogram with sides as given in the figure.
Find the distance between the sides AB and DC.
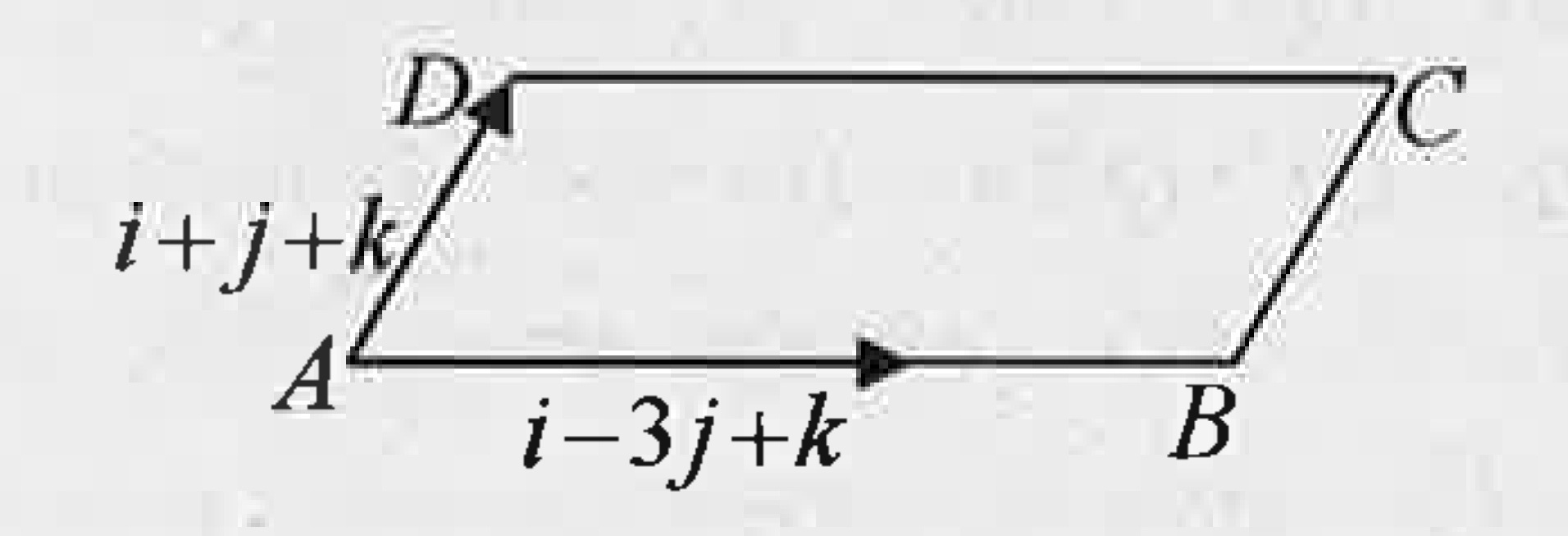
View SolutionConsider `veca=i+2j-3k,vecb=3i-j+2k,vecc=11i+2j`. Find `veca+vecb` and `veca*vecb`.
View SolutionConsider `veca=i+2j-3k,vecb=3i-j+2k,vecc=11i+2j`. Show that `veca+vecb` and `veca-vecb` are orthogonal.
View SolutionLet A (1,-1,4), B(2,1,2) and C(1,-2,-3). Find `vec(AB)`.
View SolutionLet A (1,-1,4), B(2,1,2) and C(1,-2,-3).Find the angle between `vec(AB)` and `vec(AC)`.
View SolutionLet A (1,-1,4), B(2,1,2) and C(1,-2,-3).Find the area of the parallelogram formed by `vec(AB)` and `vec(AC)` as adjacent sides.
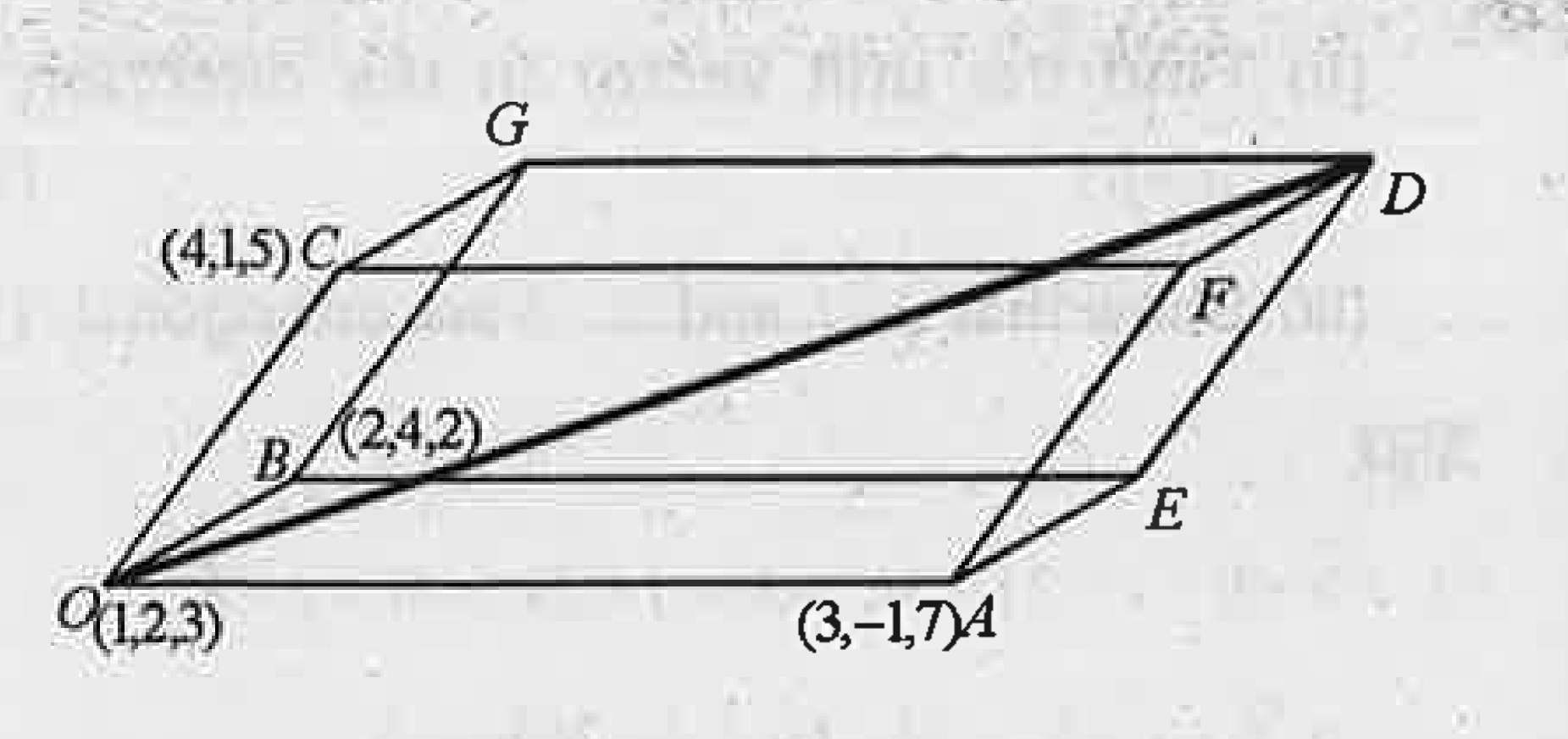
View SolutionUsing the figure following questions.
Find `vec(OD)`.
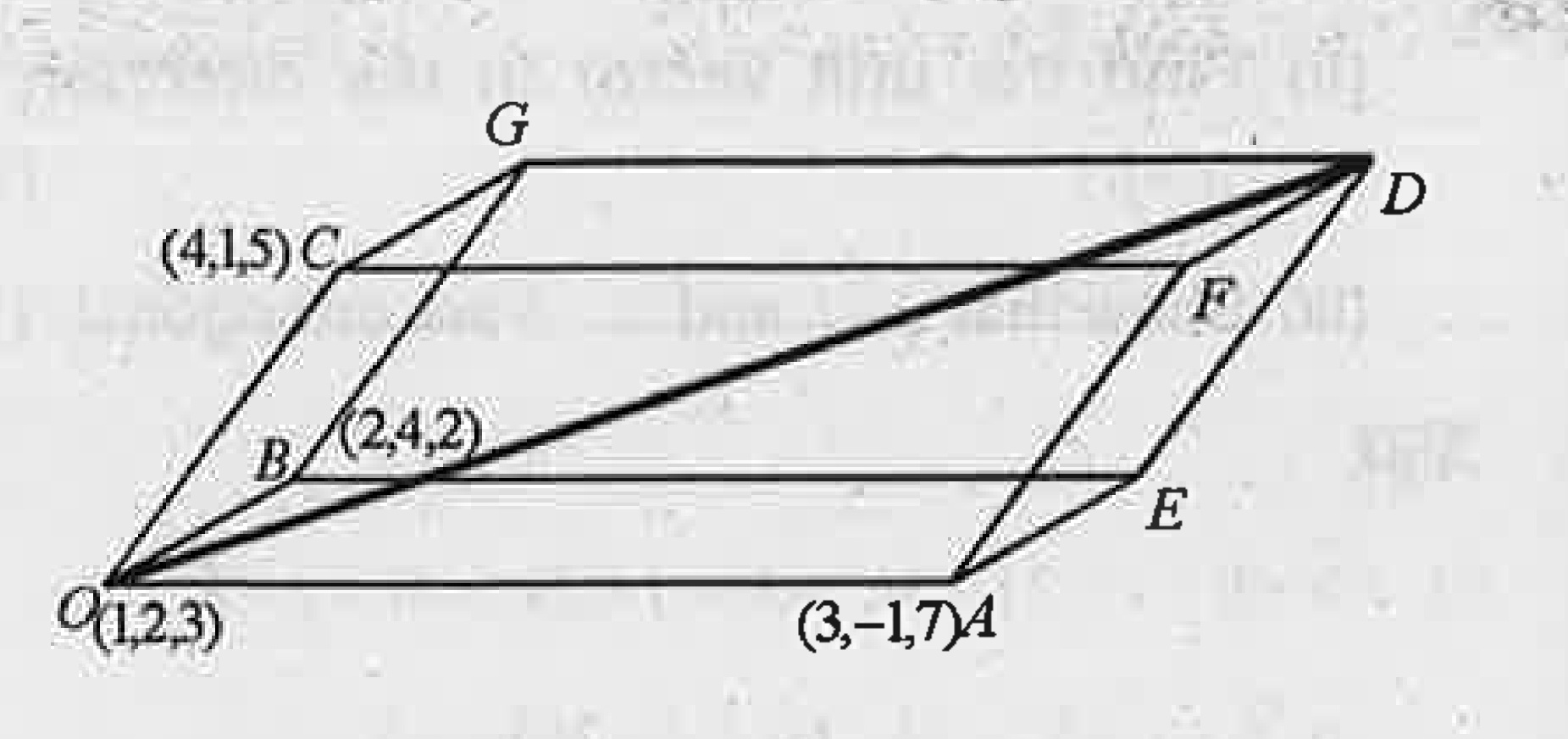
View SolutionUsing the figure following questions.
Find the coordinate of the vertexD.
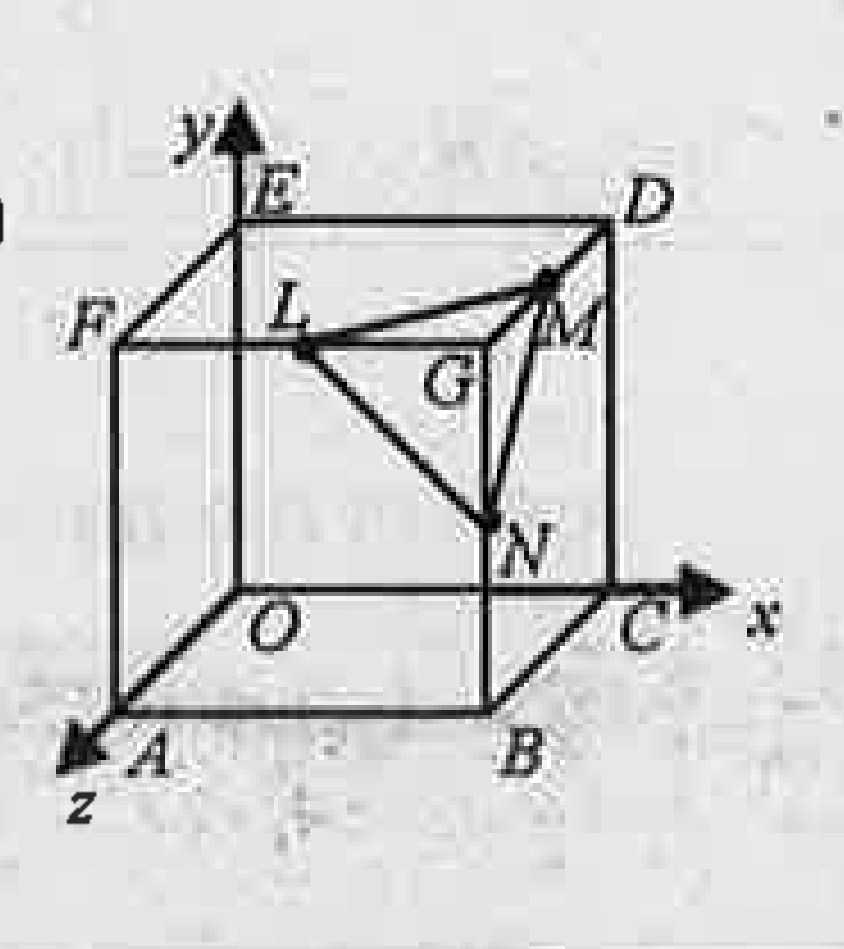
View SolutionOABCDEFG is acube with edges of length 8 units and axes are shown. L,M,N are midpoints of the edges FG, GD, GB respectively.
Find p.v's of F,B,D and G.
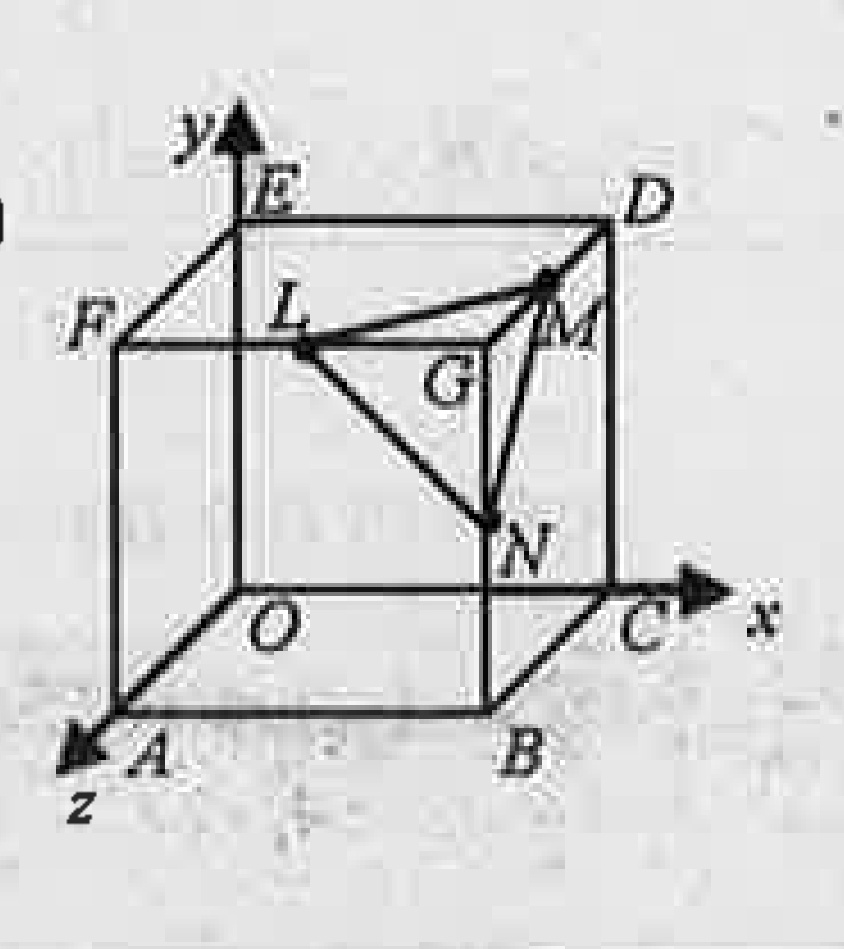
View SolutionOABCDEFG is acube with edges of length 8 units and axes are shown. L,M,N are midpoints of the edges FG, GD, GB respectively.
Show that the angle between the main diagonis is `theta=cos^-1(1/3)`
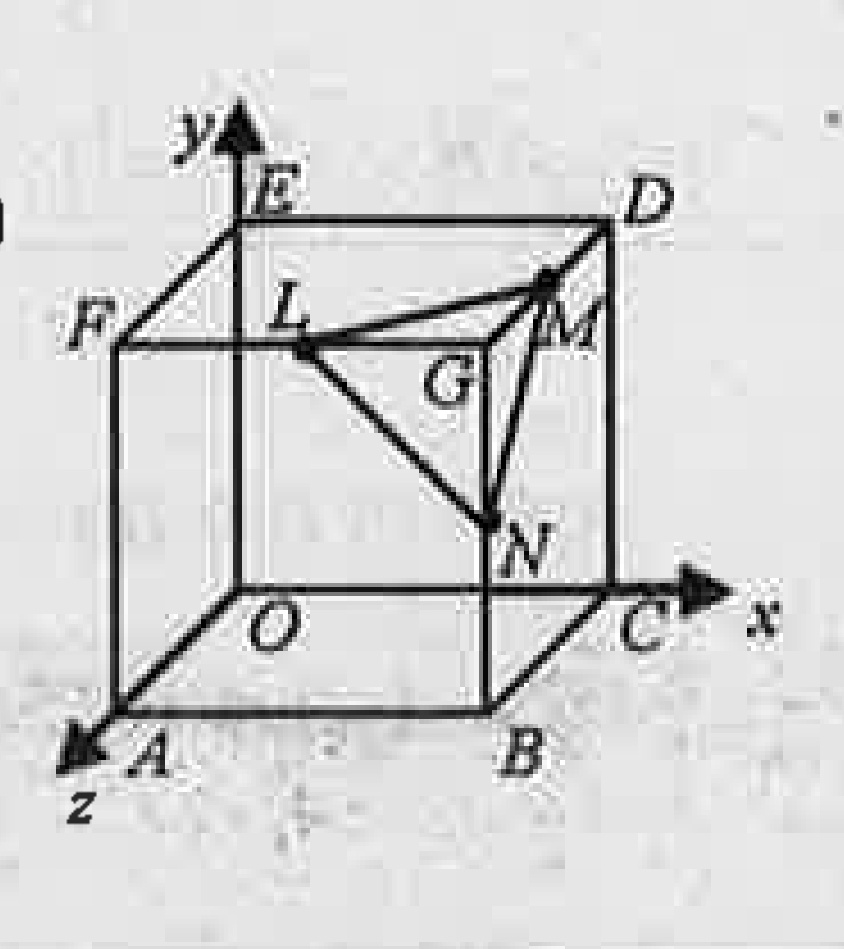
View SolutionOABCDEFG is acube with edges of length 8 units and axes are shown. L,M,N are midpoints of the edges FG, GD, GB respectively.
Find the p.v's of L,M,N.
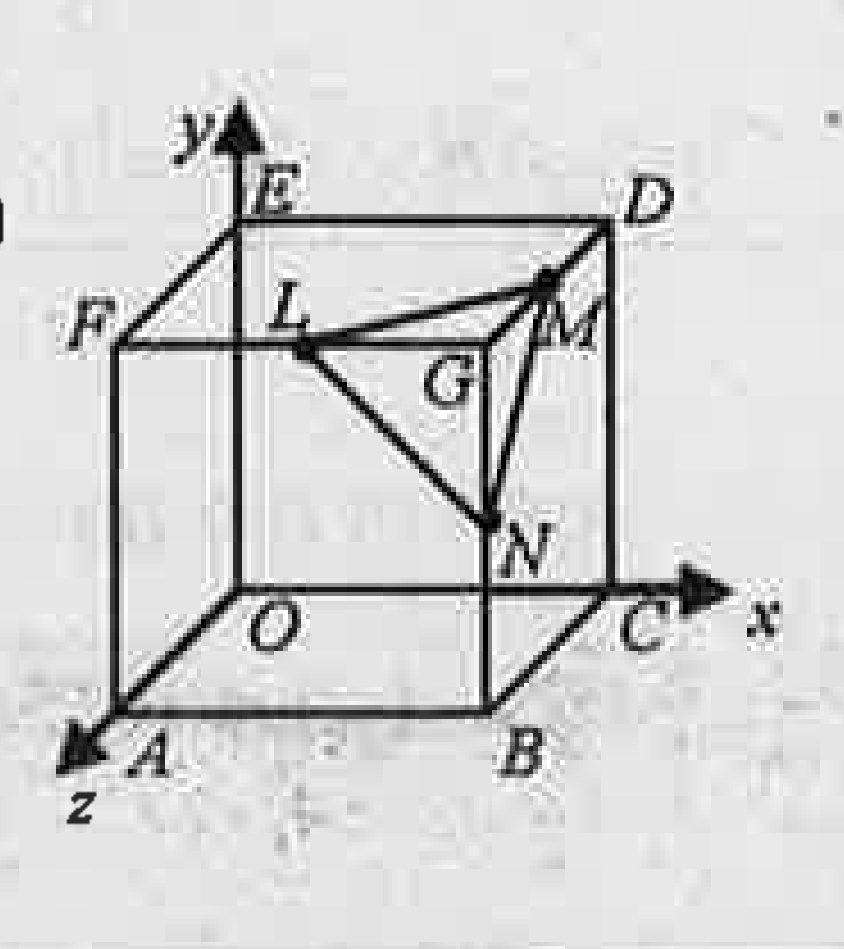
View SolutionOABCDEFG is acube with edges of length 8 units and axes are shown. L,M,N are midpoints of the edges FG, GD, GB respectively.
Show that `vec(LM)+vec(MN)+vec(NL)=0`
View SolutionUsing the figure answer the following questions
Find `vec(AD)`
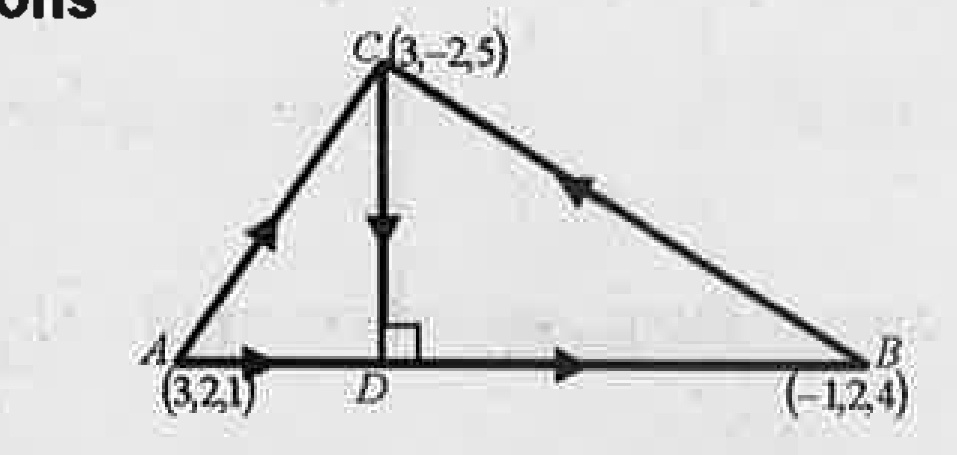
View SolutionUsing the figure answer the following questions
Find the coordinate of D.
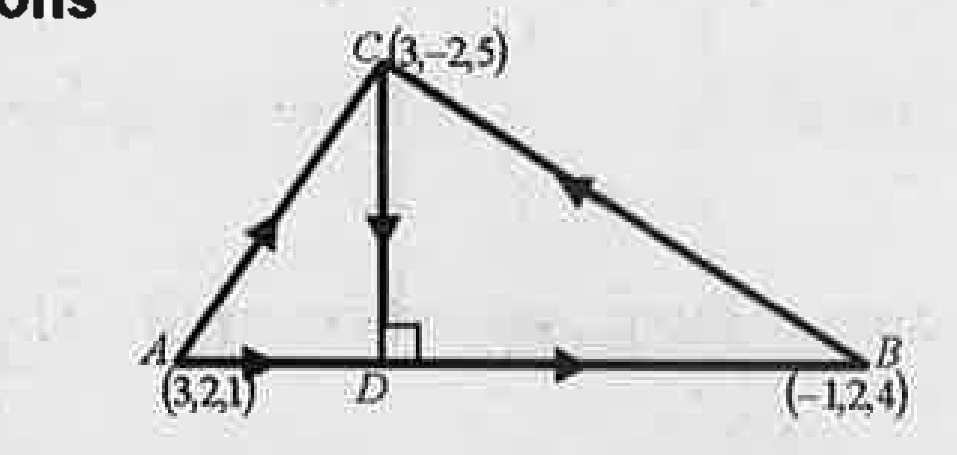
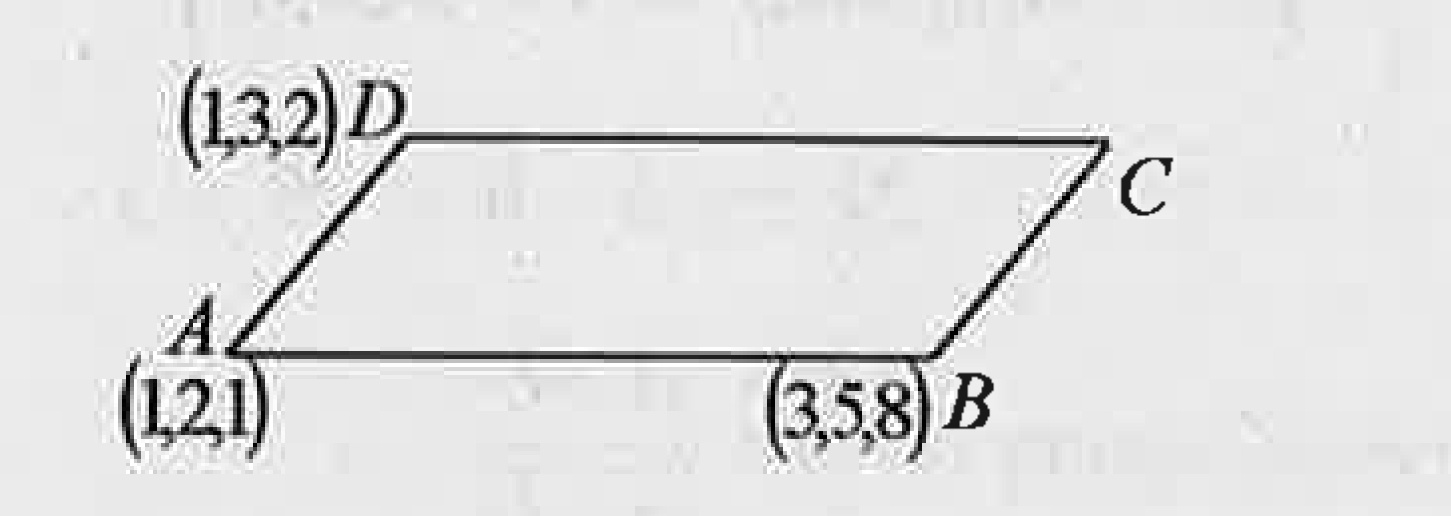
View SolutionConsider the parallelogram ABCD .Find `vec(AB)` and `vec(AD)`
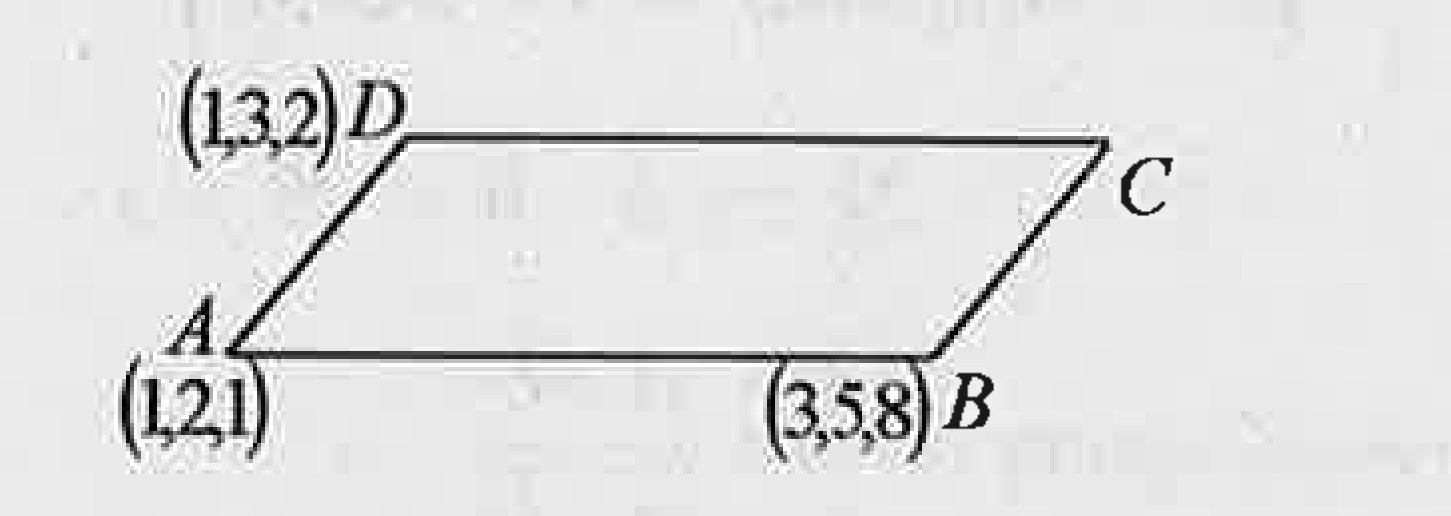
View SolutionConsider the parallelogram ABCD.Find the area of the parallelogram ABCD.

View SolutionConsider the parallelogram ABCD.Find `vec(AC)`.
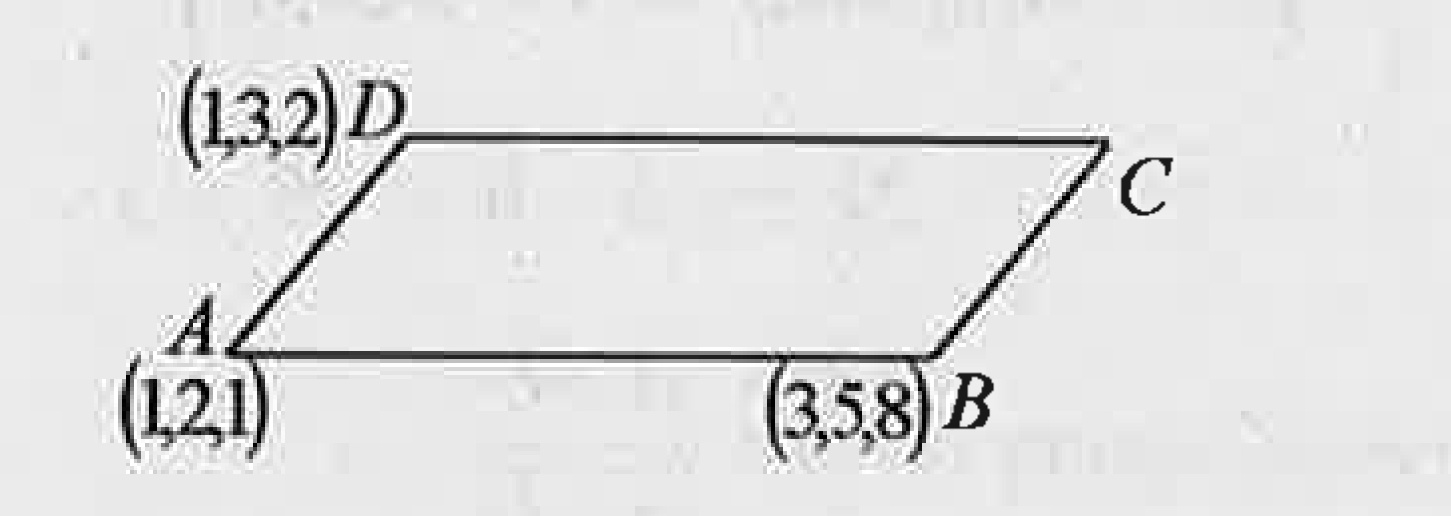
View SolutionConsider the parallelogram ABCD.Find coordinate of C.
View SolutionConsider the following quadrilateral ABCD in which P,Q,R,S are the mid points of the sides.
Find `vec(PQ)` and `vec(SR)` in terms of `vec(AC)`.
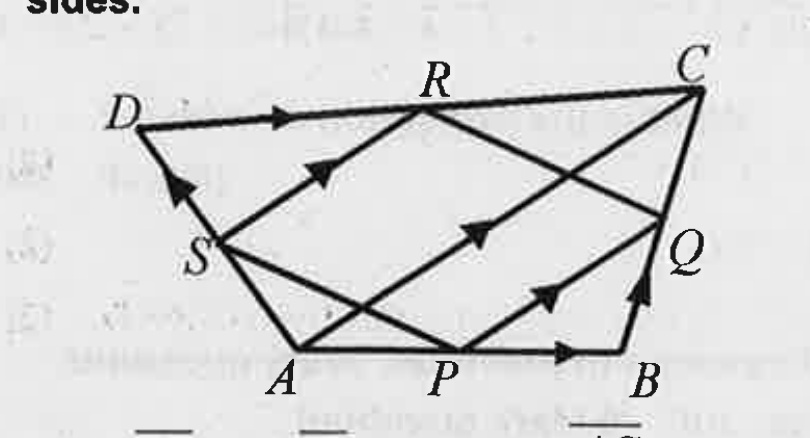
View SolutionConsider the following quadrilateral ABCD in which P,Q,R,S are the mid points of the sides.
Show that PQRS is a parallelogram.
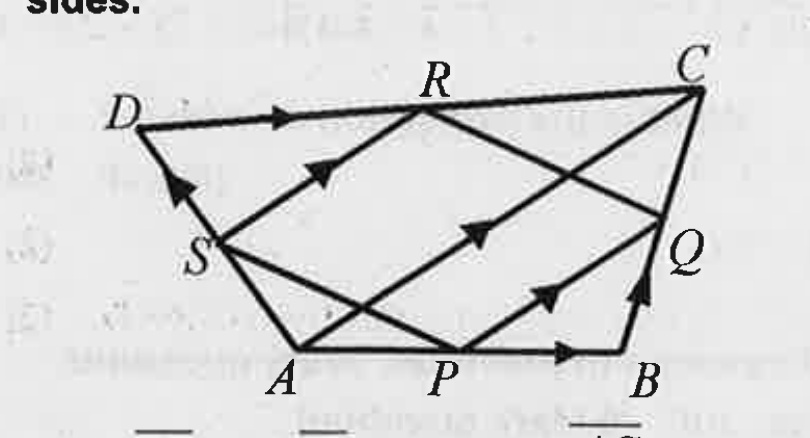
View SolutionConsider the following quadrilateral ABCD in which P,Q,R,S are the mid points of the sides.
If `veca` is any vector, prove that `veca=(veca*i)i+(veca*j)j+(veca*k)k`.
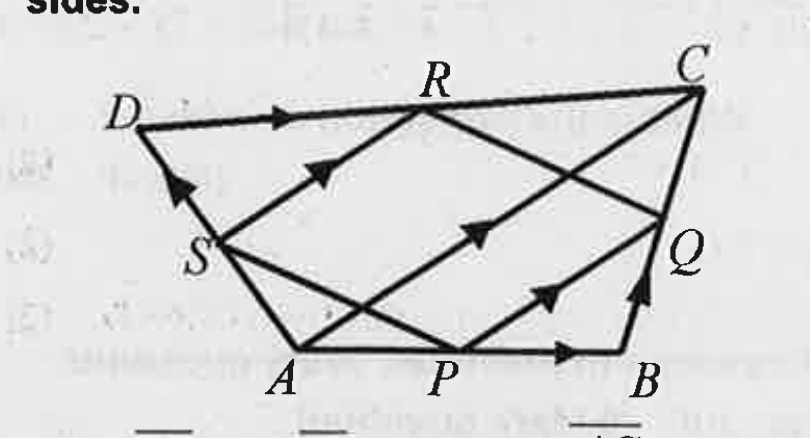
View SolutionWith help of a suitable figure for any three vectors `veca,vecb and vecc` show that `(veca+vecb)+vecc=veca+(vecb+vecc)`
View SolutionIf `veca=i-j+k` and `vecb=2i-2j-k`. What is the projection of `veca` on `vecb`?
View SolutionIf `veca=3i-j-5k` and `vecb=i-5j+3k` Show that `veca+vecb` and `veca-vecb` are perpendicular.
View SolutionGiven the position vectors of three points as `A(i-j+k),B(4i+5j+7k)C(3i+3j+5k)` Find `vec(AB)` and `vec(BC)`.
View SolutionGiven the position vectors of three points as `A(i-j+k),B(4i+5j+7k)C(3i+3j+5k)`. Prove that A,B and C are collinear points.
View SolutionWrite the unit vector in direction of `i+2j-3k`.
View SolutionIf `vec(PQ)=3i+2j-k` and the coordinate of P are (1,-1,2), find the coordinates of Q.
View SolutionThe angle between the vectors `veca` and `vecb` such that `absveca=absvecb=sqrt2` and `veca.vecb=1` is
View SolutionFind the unit vector along `veca-vecb` where `veca=i+3j-k` and `vecb=3i+2j+k`.
View SolutionConsider the vectors `veca=2i+j-2k` and `vecb=6i-3j+2k`.Find `veca.vecb` and `vecatimesvecb`.
View SolutionConsider the vectors `veca=2i+j-2k` and `vecb=6i-3j+2k`.Verify that `abs(vecatimesvecb)^2=abs(veca)^2abs(vecb)^2-(veca.vecb)^2`
View SolutionFor any three vectors `veca,vecb,vecc,` show that `vecatimes(vecb+vecc)+vecbtimes(vecc+veca)+vecctimes(veca+vecb)=0 `
View SolutionGiven `A(1,1,1),B(1,2,3),C(2,3,1)` are the vertices of `triangleABC` a triangle. Find the area of the `triangleABC`.
View SolutionConsider `A(2,3,4),B(4,3,2) and C(5,2,-1)` be any three points.
Find the projection of `vec(BC)` on `vec(AB)`.
View SolutionConsider `A(2,3,4),B(4,3,2) and C(5,2,-1)` be any three points. Find the area of triangle ABC.
View SolutionFind the angle between the vectors `veca=3i+4j+k` and `vecb=2i+3j-k`.
View SolutionThe adjacent sides of a parallelogram are `veca=3i+lambdaj+4k` and `vecb=i-lambdaj+k`. Find `vecatimesvecb`
View SolutionThe adjacent sides of a parallelogram are `veca=3i+lambdaj+4k` and `vecb=i-lambdaj+k`.If the area of the parallelogram is `sqrt42` square units, find the value of `lambda`.
View SolutionLet `veca=2i-j+2k` and `vecb=6i+2j+3k`.Find a unit vector in the direction of `veca+vecb`.
View SolutionLet `veca=2i-j+2k` and `vecb=6i+2j+3k`
Find the angle between `veca` and `vecb`.
View SolutionConsider the triangle ABC with vertices A(1,1,1), B(1,2,3) and C(2,3,1)
Find `vec(AB)` and `vec(AC)`.
View SolutionConsider the triangle ABC with vertices A(1,1,1), B(1,2,3) and C(2,3,1).Find `vec(AB)timesvec(AC)`.
View SolutionConsider the triangle ABC with vertices A(1,1,1), B(1,2,3) and C(2,3,1).Hence find the area of the triangle.
View SolutionConsider the vectors
`veca=i-7j+7k,vecb=3i-2j+2k`.
Find `veca.vecb`.
View SolutionConsider the vectors `veca=i-7j+7k,vecb=3i-2j+2k`.Find the angle between `veca` and `vecb`.
View SolutionConsider the vectors
`veca=i-7j+7k,vecb=3i-2j+2k`.
Find the area of parallelogram with adjacent sides `veca` and `vecb`.
View SolutionIf the points A and B are (1,2,-1) and (2,1,-1) respectively, then `vec(AB)` is
View SolutionFind the value of `lambda` for which the vectors `2i-4j+5k`, `i-lambdaj+k` and `3i+2j-5k` are coplanar.
View SolutionFind the angle between the vectors `veca=2i+j-k` and `vecb=i-j+k`.
View Solution`(veca-vecb)times(veca+vecb)` is equal to a)`veca` b)`abs(veca)^2-abs(vecb)^2` c)`vecatimesvecb` d)`2(vecatimesvecb)`
View SolutionUsing vectors, show that the points
`A(1,2,7),B(2,6,3),C(3,10,-1)` are collinear.
View SolutionFind a vector in the direction of `vecr=3i-4j` that has a magnitude of 9.
View SolutionFor any three vectors `veca,vecb` and `vecc`, and, prove that `(veca+vecb)+vecc=veca+(vecb+vecc)`.
View SolutionFind a unit vector perpendicular to `veca+vecb` and `veca-vecb`, where `veca=i-3j+3k` and `vecb=3i-3j+2k`.
View SolutionLet `A(2,3,4),B(4,3,2)` and `C(5,2,-1)` be three points.Find `vec(AB)` and `vec(BC)`.
View SolutionLet `A(2,3,4),B(4,3,2)` and `C(5,2,-1)` be three points .Find the projection of `vec(BC)` on `vec(AB)`.
View SolutionLet `A(2,3,4),B(4,3,2)` and `C(5,2,-1)` be three points
Find the area of the triangle ABC.
View SolutionABCD is a parallelogram with A as the origin. `vecb` and `vecd` are position vector of B and D respectively. What is the position of vector C?

View SolutionABCD is a parallelogram with A as the origin. `vecb` and `vecd` are position vector of B and D respectively.What is the angle between `vec(AB)` and `vec(AD)`?

View SolutionABCD is a parallelogram with A as the origin. `vecb` and `vecd` are position vector of B and D respectively.
If `absvec(AC)=absvec(BD)`, show that ABCD is a Rectangle.

View SolutionIf `veca,vecb,vecc,vecd` respectively are the position vectors representing the vertices A,B,C,D of a parallelogram, then write `vecd` in terms of `veca,vecb,vecc`.
View SolutionFind the projection vector of
`vecb=i+2j+k` along the vector
`veca=2i+j+2k`. Also write `vecb` as the sum of a vector along `veca` and a parpendicular to `veca`.
View Solution
EXAMPLE questions and complete solutions for chapter VECTOR ALGEBRA of MAXIMUM PUBLICATION of Class 12