Complete Solutions to EXAMPLE of chapter THREE DIMENSIONAL GEOMETRY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | THREE DIMENSIONAL GEOMETRY |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Consider the lines `barr=(hati+2hatj+3hatk)+lambda(2hati-3hatj-4hatk)` , `barr=(hati+hatj+hatk)+mu(hati+3hatj+2hatk)`
Write the Cartesian equation.
View SolutionConsider the lines `barr=(hati+2hatj+3hatk)+lambda(2hati-3hatj-4hatk)` , `barr=(hati+hatj+hatk)+mu(hati+3hatj+2hatk)`
Find the angle between the lines.
View SolutionFind the vector equation of the plane passing through the intersection of the planes `barr.(hati+hatj+hatk)=6` and `barr.(2hati+3hatj+4hatk)=-5` at the point (1,1,1) .
View SolutionFind the equation of the plane passing through the intersection of the planes
`x+y+4z+5=0` and `2x-y+3z+6=0` and contains the point (1,0,0).
View SolutionConsider the point (-1,-2,-3). In which octant ,the above point lies.
View SolutionFind the direction cosines of the line joining (-1,-2,-3) and (3,4,5) .
View SolutionIf P is any point such that `OP=sqrt(50)` and direction cosines of OP are `3/(sqrt50)` , `4/(sqrt50)` and `5/(sqrt50)` , then find the co-ordinate of P.
View SolutionConsider a cube of side 'a' unit has one vertex at the origin O.
Write down the co-ordinate O, O' , A and A'

View SolutionConsider a cube of side 'a' unit has one vertex at the origin O.
Find the direction ratios of OO' and AA' .
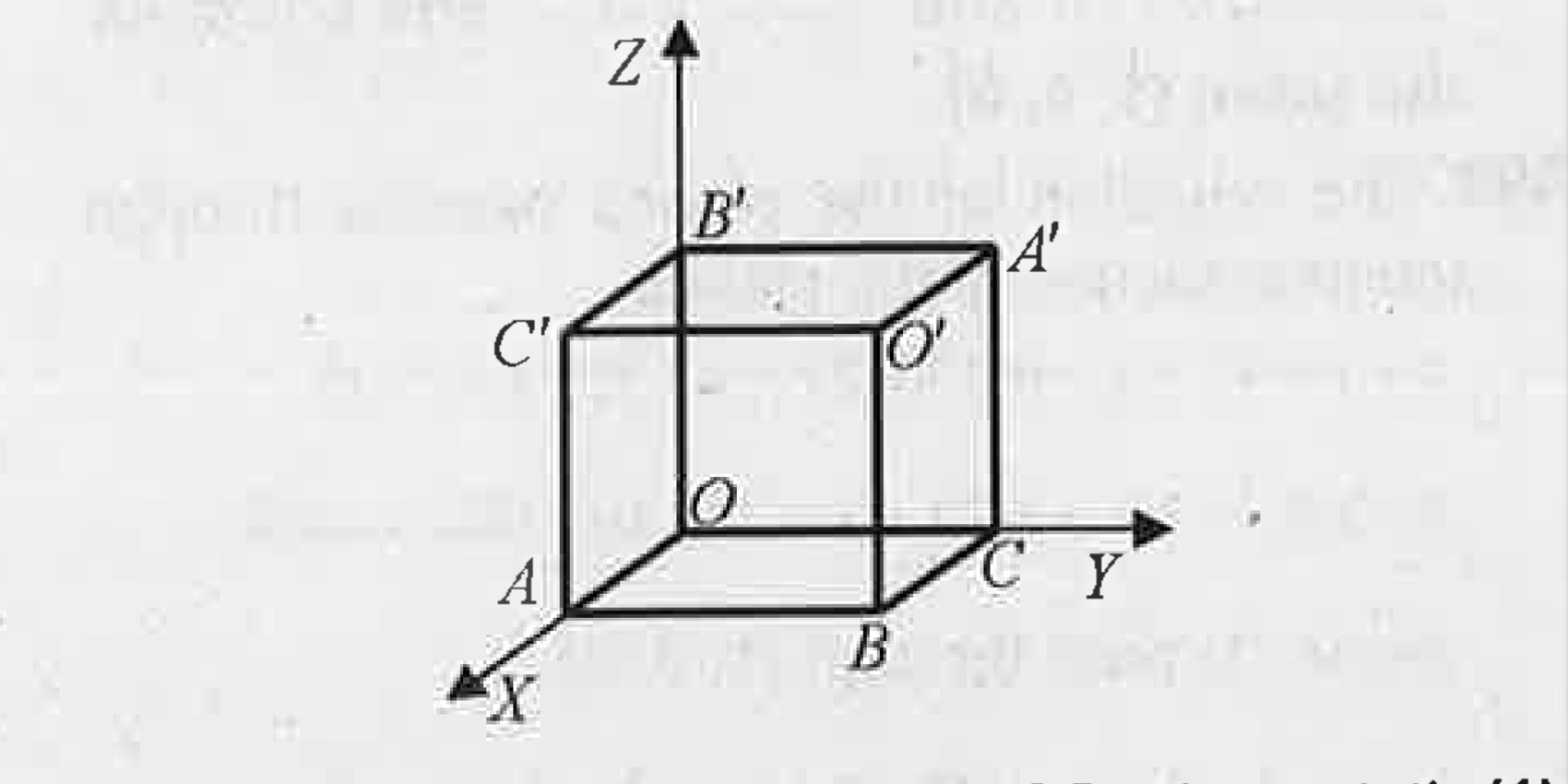
View SolutionConsider a cube of side 'a' unit has one vertex at the origin O.
Show that the angle between the main diagonals of the above cube is `cos^-1(1/3)`

View SolutionConsider two points A and B and a line L as shown in figure.
Find `bar(AB)`
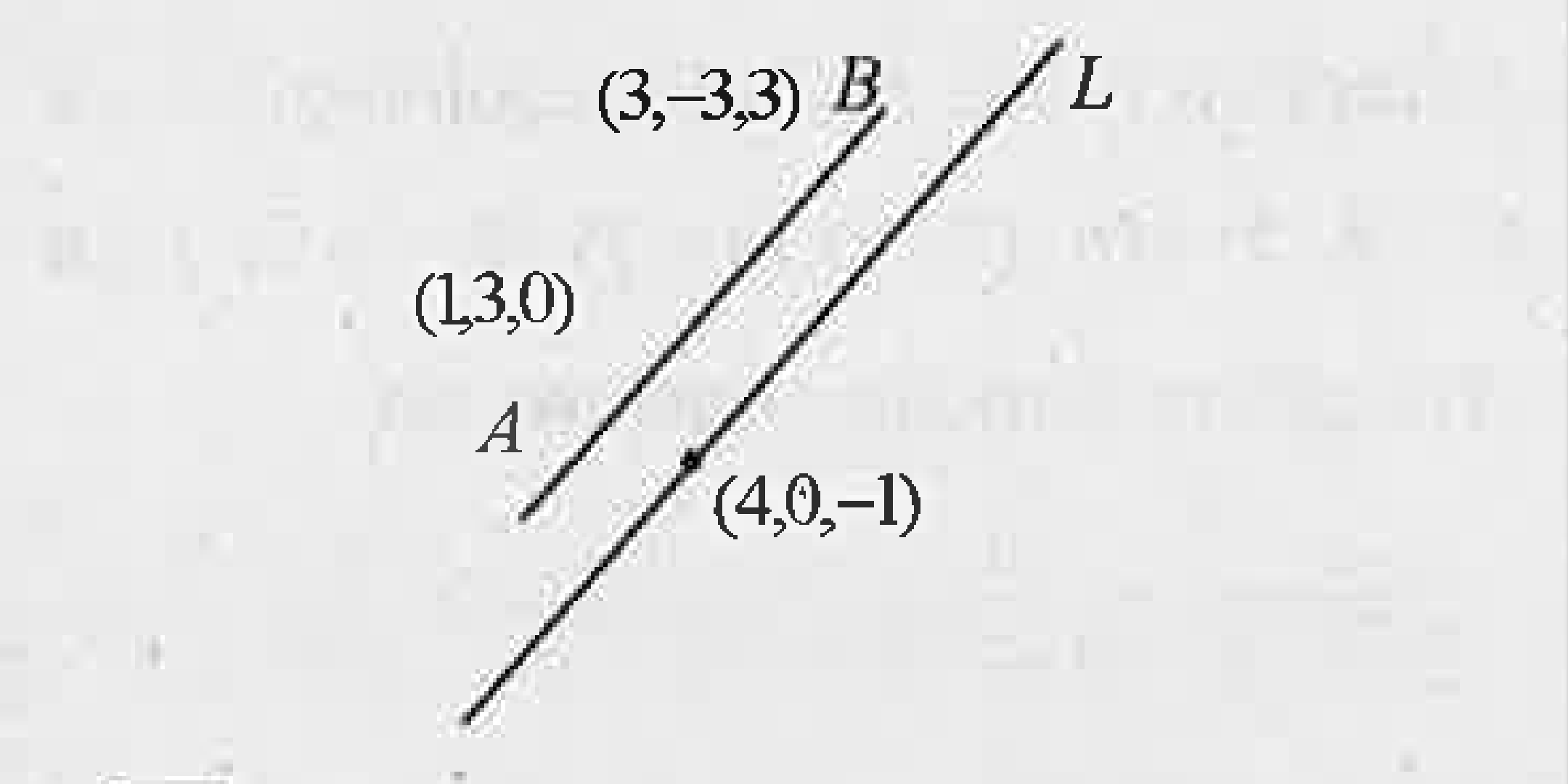
View SolutionConsider two points A and B and a line L as shown in figure.
Find the Cartesian equation of the line L.
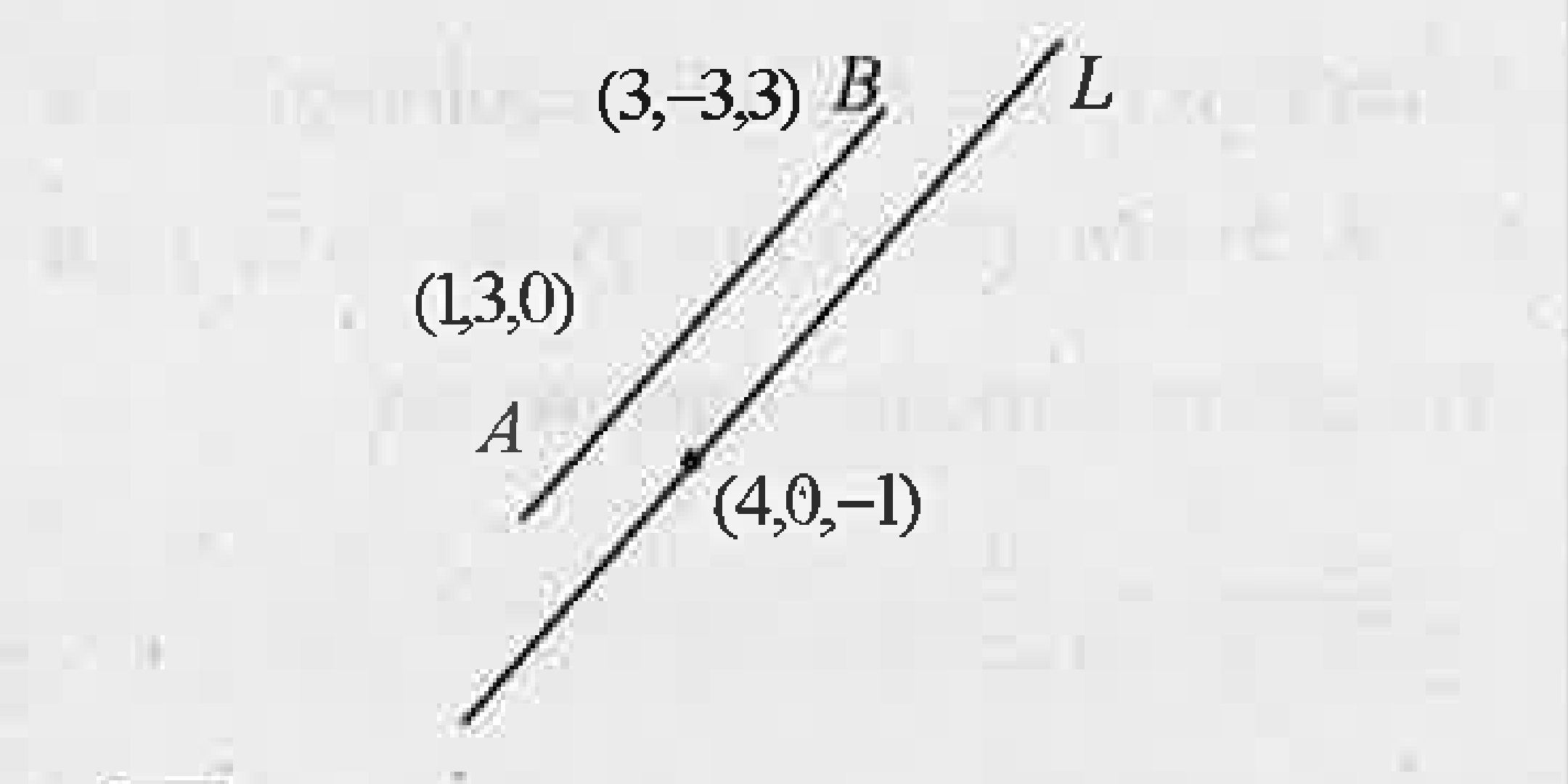
View SolutionConsider two points A and B on L1 and a line L2 as shown in figure. `Find the foot of the perpendicular drawn from (2,3,4) on L1 to the line L2.

View SolutionCartesian equation of two lines are `(x+2)/2=(y+2)/4=(z+2)/1` , `(x-1)/2=(y-1)/-3=(z-1)/-4`.Write the vector equation of the lines.
View SolutionCartesian equation of two lines are `(x+2)/2=(y+2)/4=(z+2)/1` , `(x-1)/2=(y-1)/-3=(z-1)/-4`.find the shortest distance between the lines.
View SolutionConsider the points P(1,3,4) &Q(-3,5,2) .Find the equation of the line passing through P and Q.
View SolutionConsider the points (1,3,4) &(-3,5,2). At which point that the above line cuts the plane `2x+y+z+3=0` .
View SolutionLet the equation of a plane be `barr.(2hati-3hatj+5hatk)=7`, then find the Cartesian equation of the plane.
View SolutionLet the equation of a plane be `barr.(2hati-3hatj+5hatk)=7`, then find the equation of a plane passing through the point (3,4,-1) and parallel to the given plane .
View SolutionLet the equation of a plane be `barr.(2hati-3hatj+5hatk)=7`, then find the equation of a plane passing through the point (3,4,-1) and parallel to the given plane .
View SolutionState the condition of the line `barr=bara+lambdabarb` is parallel to the plane `barr.barn=d` .
View SolutionShow that the line `barr=i+j+lambda(2i+j+4k)` is parallel to the plane `barr.(-2i+k)=5` .
View SolutionFind the distance between the line `barr=i+j+lambda(2i+j+4k)` and the plane `barr.(-2i+k)=5` .
View SolutionIf a line in the space makes angle `alpha,beta` and `gamma` with the coordinates axes, then `cos^2alpha+cos^2beta+cos^2gamma` is equal to a)1 b)2 c)0 d)3
View SolutionThe direction ratios of the line `(x-6)/1=(2-y)/2=(z-2)/2`are a)6,-2,-2 b)1,2,2 c)6,1,-2 d)0,0,0
View SolutionIf the vector equation of a line is
`barr=i+j+k+mu(2i-3j-4k)` , then the Cartesian equation of the line is
View SolutionIf the Cartesian equation of a plane is `x+y+z=12` , then the vector equation of the plane is.... a)`barr.(2i+j+k)=12` b)`barr.(i+j+k)=12`
c)`barr.(i+j+2k)=12` d)`barr.(i+3j+k)=12`
View SolutionConsider the lines `barr=(i+2j-2k)+lambda(i+2j)`
and `barr=(i+2j-2k)+mu(2j-k)`
Find the angles between the lines.
View SolutionConsider the lines `barr=(i+2j-2k)+lambda(i+2j)`
and `barr=(i+2j-2k)+mu(2j-k)`
Find a vector perpendicular to both the lines.
View SolutionConsider the lines `barr=(i+2j-2k)+lambda(i+2j)`
and `barr=(i+2j-2k)+mu(2j-k)`
Find the equation of the line passing through the point of intersection of lines and perpendicular to both the lines.
View SolutionConsider the line `barr=(2i-j+k)+lambda(i+2j+3k)`. Find the Cartesian equation of the line.
View SolutionConsider the line `barr=(2i-j+k)+lambda(i+2j+3k)`
Find the vector equation of the line passing through A (1,0,2) and parallel to the line.
View SolutionConsider the line `barr=(2i-j+k)+lambda(i+2j+3k)`
Write two points on the line obtained from vector equation of the line passing through A (1,0,2) and parallel to the line which are equidistant from A.
View SolutionFind the equation of the plane through the point (1,2,3) and perpendicular to the plane `x-y+z=2` and `2x+y-3z=5`
View SolutionFind the distance between the planes
`x-2y+2z-8=0` and `6y-3x-6z=57`
View SolutionConsider the Cartesian equation of line `(x-3)/2=(y+1)/3=(z-5)/-2` Find the vector equation of the line.
View SolutionConsider the Cartesian equation of line
`(x-3)/2=(y+1)/3=(z-5)/-2`
Find its intersecting point with the plane
`5x+2y-6z-7=0`
View SolutionConsider the Cartesian equation of line
`(x-3)/2=(y+1)/3=(z-5)/-2`
Find the angle made by the line with the plane `5x+2y-6z-7=0`
View SolutionFrom the following figure
Find `vec(AB)`
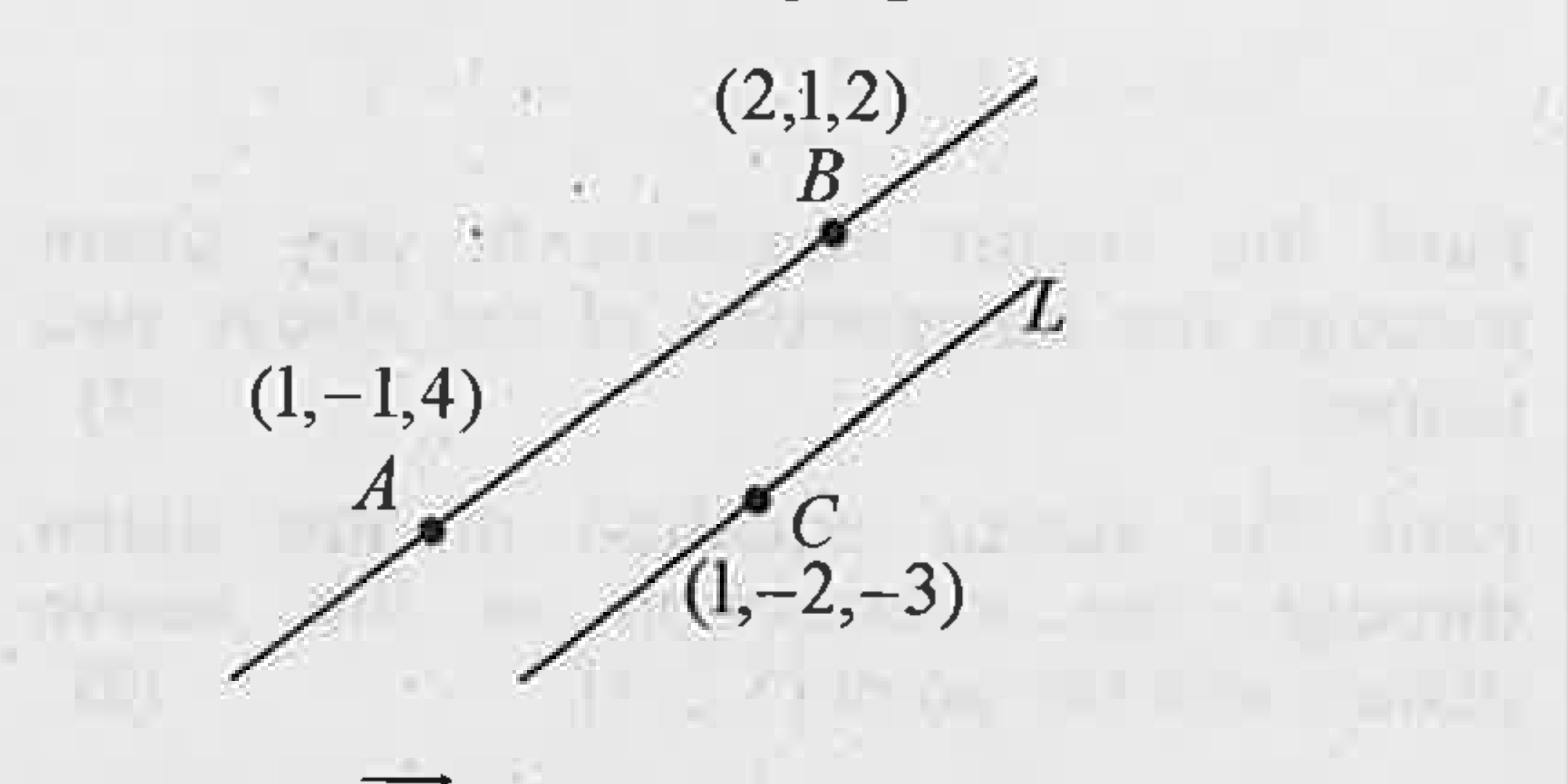
View SolutionFrom the following figure
Find the vector equation of line L.
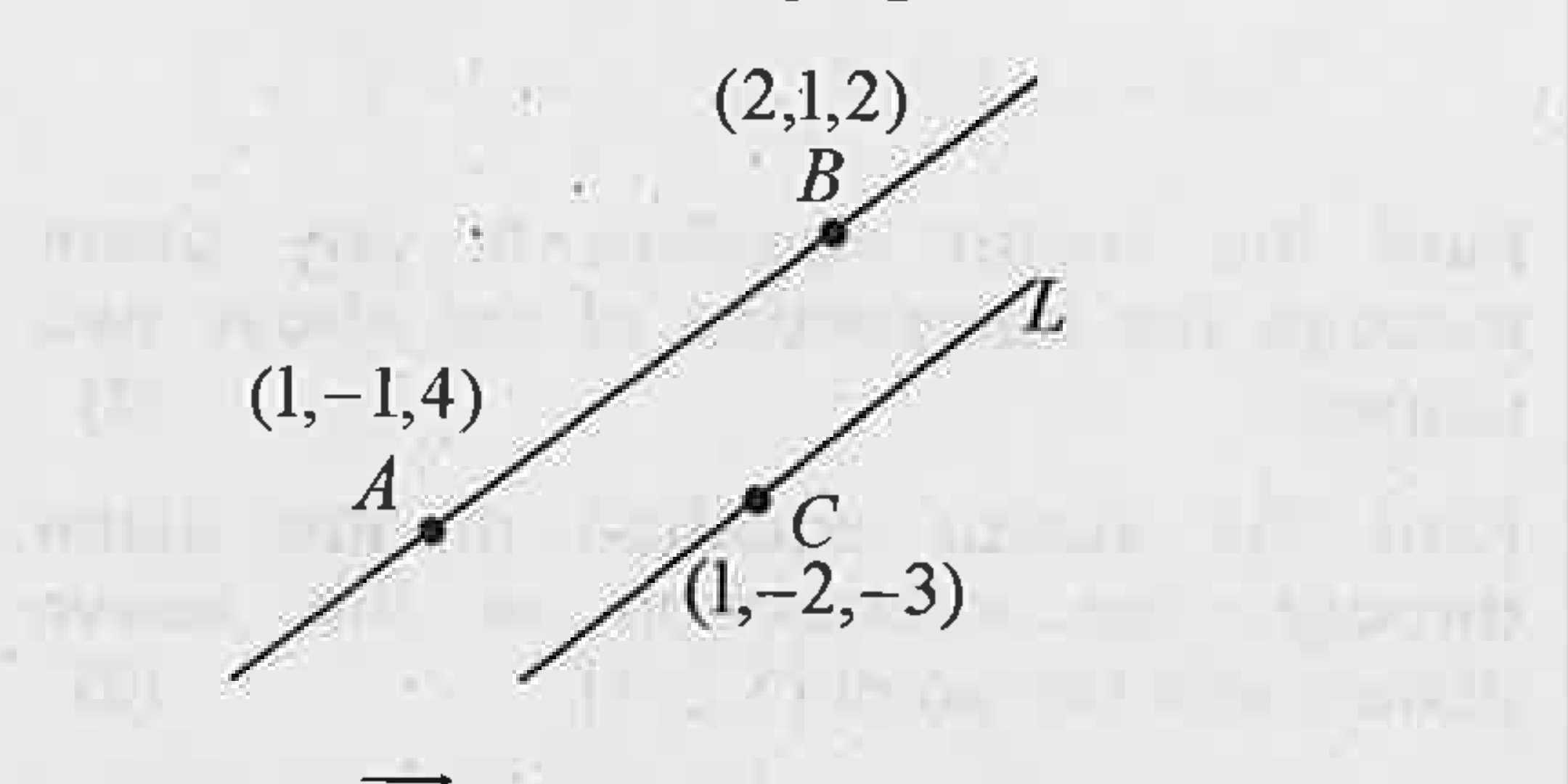
View SolutionFrom the following figure
Find a point on line L other than C.

View SolutionFind the vector equation of the plane which is at a distance of `6/sqrt(29)` from the origin with perpendicular vector `2i-3j+4k` . Convert into Cartesian form. Also find the foot of the perpendicular drawn from the origin to the plane.
View SolutionConsider the Plane `barr.(-6i-3j-2k)+1=0`. find the direction cosines perpendicular to the plane and perpendicular distance from the origin.
View SolutionConsider three points (6,-1,1), (5,1,2) and (1,-5,-4) on space. Find the Cartesian equation of the plane passing through these points .
View SolutionConsider three points (6,-1,1), (5,1,2) and (1,-5,-4) on space. Find directions ratios normal to the Planes
View SolutionConsider three points (6,-1,1), (5,1,2) and (1,-5,-4) on space. Find a unit vector normal to the plane.
View SolutionConsider a straight line through a fixed point with position vectors 2i-2j+3k and parallel to i-j+4k .
Write down the vector equation of the straight line.
View SolutionConsider a straight line through a fixed point with position vectors 2i-2j+3k and parallel to i-j+4k .
Show that the straight line is parallel to the plane `barr.(i+5j+k)=5`
View SolutionConsider a straight line through a fixed point with position vectors 2i-2j+3k and parallel to i-j+4k .
Find the distance between the line and plane `barr.(i+5j+k)=5`
View SolutionConsider the vector equation of two planes
`barr.(2i+j+k)=3,barr(i-j-k)=4`
Find vector equation of any plane through the intersection of the above two planes.
View SolutionConsider the vector equation of two planes `barr.(2i+j+k)=3,barr.(i-j-k)=4` Find vector equation of the plane through the intersection of the above planes and the point (1,2,-1).
View SolutionDistance of the point(0,0,1) from the plane `x+y+z=3` a)`1/sqrt3`units b)`2/sqrt3`units c)`sqrt3`units d)`sqrt3/2`units
View SolutionFind the equation of the plane through the line of intersection of the planes x+y+z=1 and 2x+3y+4z=5 which is perpendicular to x-y+z=0
View SolutionConsider a plane `barr.(6i-3j-2k)+1=0`
Find dc's perpendicular to the plane.
View SolutionConsider a plane `barr.(6i-3j-2k)+1=0`
Find a vector of magnitude 14 units perpendicular to given plane.
View SolutionConsider a plane `barr.(6i-3j-2k)+1=0`.Find the equation of a line parallel to the above vector and passing through the point (1,2,1).
View SolutionConsider the pair of lines whose equations are . `(x-2)/2=(y-1)/5=(z+3)/-3` and `(x+1)/-1=(y-4)/8=(z-5)/4`
Write the direction ratios of the lines.
View SolutionConsider the pair of lines whose equations are . `(x-2)/2=(y-1)/5=(z+3)/-3` and `(x+1)/-1=(y-4)/8=(z-5)/4`
Find the shortest distance between the above skew lines.
View SolutionConsider the pair of lines whose equations are . `(x-2)/2=(y-1)/5=(z+3)/-3` and `(x+1)/-1=(y-4)/8=(z-5)/4`
Find the angle between these two lines.
View SolutionConsider the pair of lines
`barr=3i+4j-2k+lambda(-i+2j+k)`….`L_1`,
`barr=i-7j-2k+mu(i+3j+2k)`….`L_2`
Find one point each on lines `L_1` and `L_2`.
View SolutionConsider the pair of lines
`barr=3i+4j-2k+lambda(-i+2j+k)`….`L_1`,
`barr=i-7j-2k+mu(i+3j+2k)`….`L_2`
Find one point each on lines `L_1` and `L_2`.
Find the distance between those points.
View SolutionConsider the pair of lines
`barr=3i+4j-2k+lambda(-i+2j+k)`….`L_1`,
`barr=i-7j-2k+mu(i+3j+2k)`….`L_2`
Find the shortest distance between `L_1` and `L_2`
View SolutionConsider the points A(2,2,-1), B(3,4,2) and C(7,0,6) Are A,B and C collinear? Explain.
View SolutionConsider the points A(2,2,-1), B(3,4,2) and C(7,0,6).Find the vector and Cartesian equation of the plane passing these three points.
View SolutionConsider the points A(2,2,-1), B(3,4,2) and C(7,0,6).
Find the vector and Cartesian equation of the plane passing these three points.
Find the angle between the above plane and the line `barr=(i+2j-k)+lambda(i-j+k)`
View SolutionConsider three points on space (2,1,0),(3,-2,-2) and (3,1,7). Find the Cartesian equation of the plane passing through the above points.
View SolutionConsider three points on space (2,1,0),(3,-2,-2) and (3,1,7).Find the Cartesian equation of the plane passing through the above points.Convert the equation into vector form.
View SolutionConsider three points on space (2,1,0),(3,-2,-2) and (3,1,7)
Find the Cartesian equation of the plane passing through the above points.
find a unit vector perpendicular to the plane and also find the perpendicular distance of the plane from the origin..
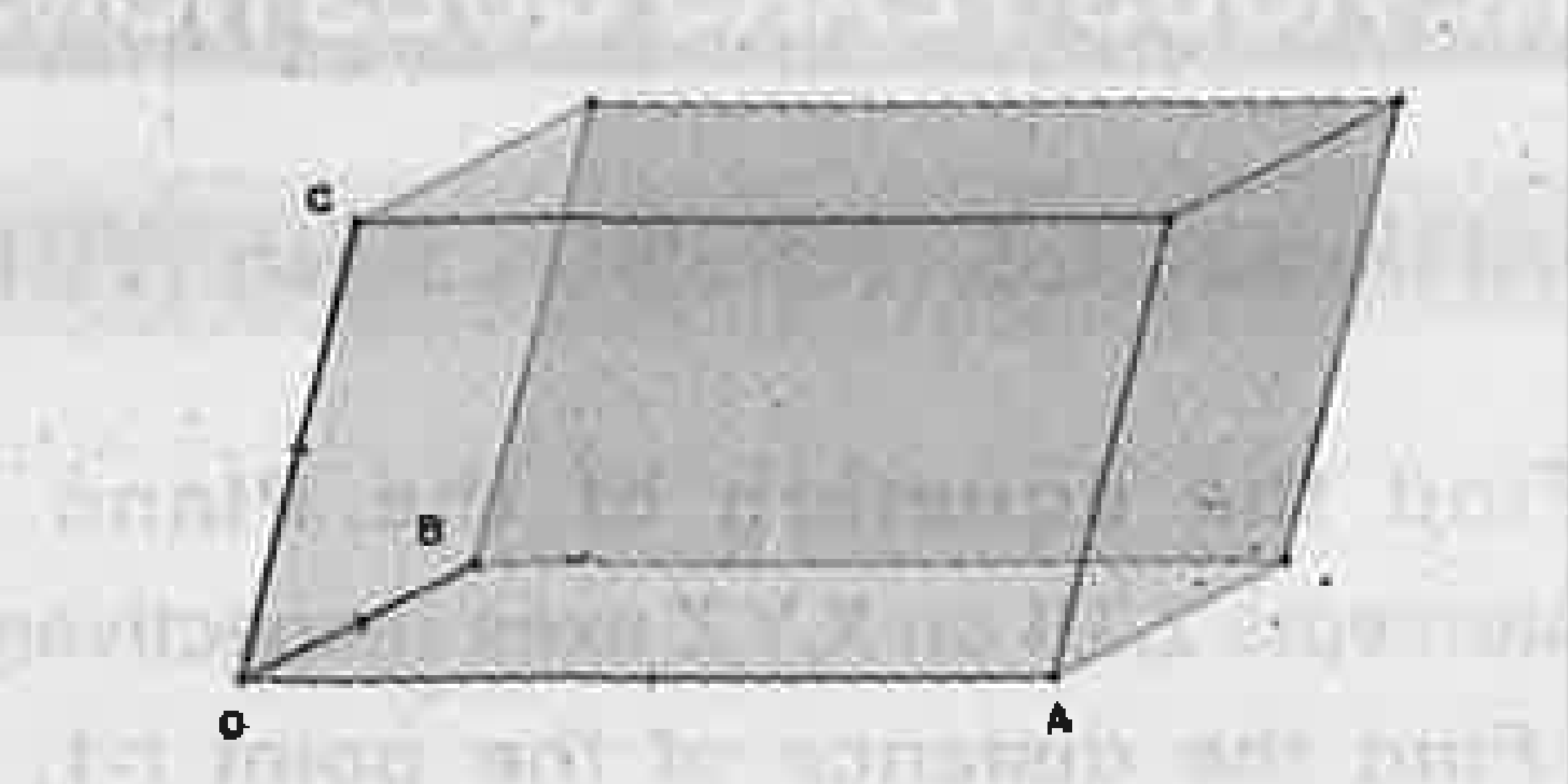
View Solution`bar(OA)=i+2j+3k`
`bar(OB)=i-2j+4k`
`bar(OC)=2i+3j+k`
are adjacent sides of the parallelopiped.
Find the base area of the parallelopiped.
(Base determined by `bar(OA)` and `bar(OB)`)
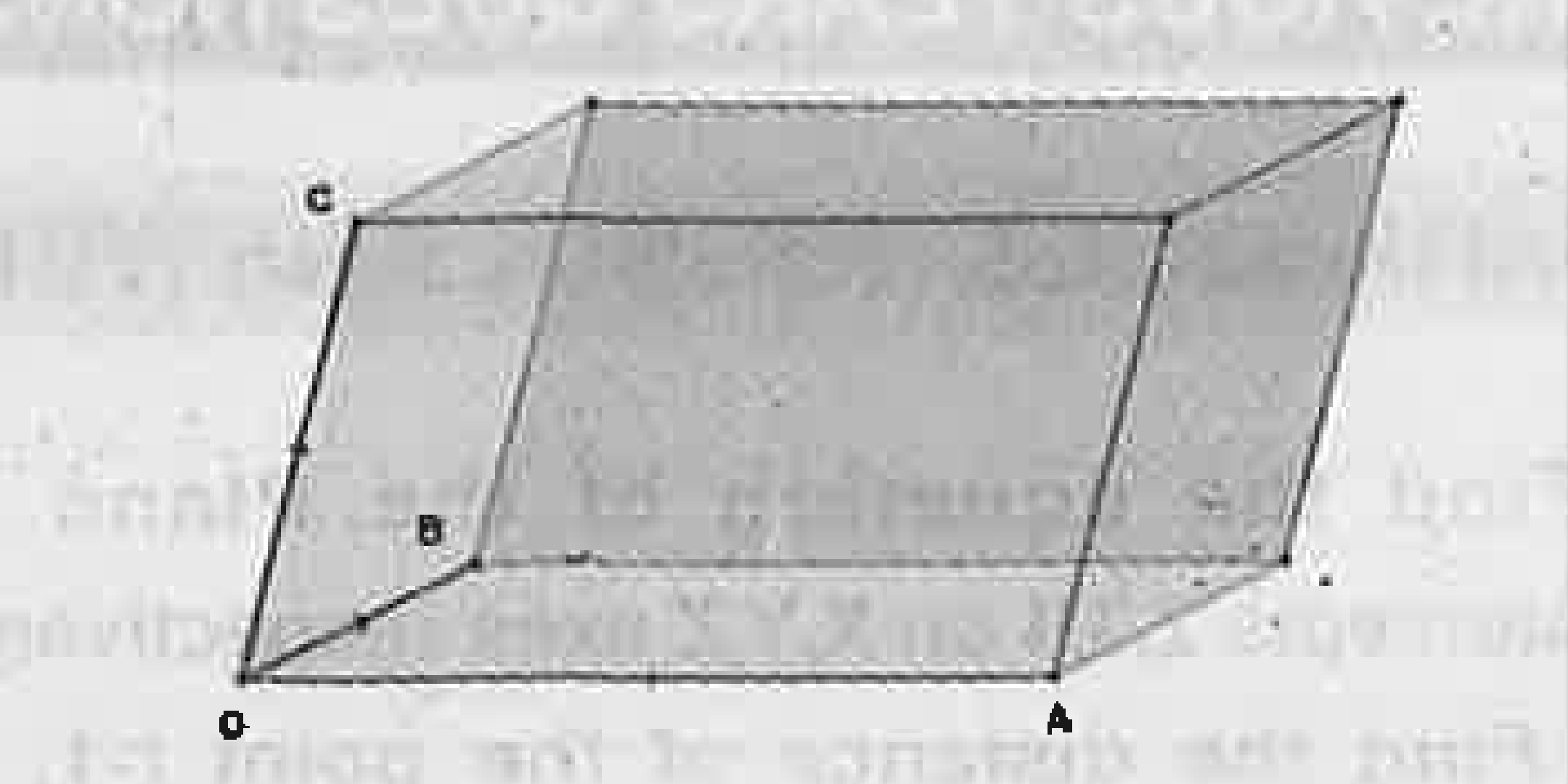
View Solution`bar(OA)=i+2j+3k`
`bar(OB)=i-2j+4k`
`bar(OC)=2i+3j+k`
are adjacent sides of the parallelopiped.
Find the volume of the parallelopiped.
View Solution`bar(OA)=i+2j+3k`
`bar(OB)=i-2j+4k`
`bar(OC)=2i+3j+k`
are adjacent sides of the parallelopiped.
Find the height of the parallelopiped.

View SolutionFind the equation of the line passing through the point (2,1,0) and (3,2,-1)
View SolutionFind the equation of the line passing through the point (2,1,0) and (3,2,-1)
Find the shortest distance of the line from the line
`barr=(i-j+2k)+lambda(2i+j-3k)`
View SolutionThe equation of two lines are `(x-1)/2=(y-2)/2=(z-3)/3` and `x/-3=y/2=z/5` , then Find the dr's of the given lines.
View SolutionThe equation of two lines are `(x-1)/2=(y-2)/2=(z-3)/3` and `x/-3=y/2=z/5` , then Find the angle between the given lines.
View SolutionThe equation of two lines are
`(x-1)/2=(y-2)/2=(z-3)/3` and `x/-3=y/2=z/5` , then
Find the equation of the line passing through (2,1,3) and perpendicular to the given lines.
View SolutionFind the direction cosine of the vector 2i+2j-k.
View SolutionFind the distance of the point (2,3,4) from the plane `barr.(3i-6j+2k)=-11` .
View SolutionFind the shortest distance between the lines `barr=(2i-j-k)+lambda(3i-5j+2k)` and `barr=(i+2j+k)+mu(i-j+k)`
View SolutionFind the equation of the Plane with intercepts 2,3,4 on X,Y,Z axes respectively.
View SolutionFind the distance of the point (-1,-2,3) from the Plane `barr.(2i-3j+4k)=4`
View SolutionConsider the points A(2,2,-1), B(3,4,2), C(7,0,6).Find AB.
View SolutionConsider the points A(2,2,-1), B(3,4,2), C(7,0,6).Find the Cartesian and vector equation of the plane passing through these points.
View SolutionConsider the points A(3,-4,-5) and B(2,-3,1)
Find the vector and Cartesian equation of the line passing through the points A and B.
View SolutionConsider the points A(3,-4,-5) and B(2,-3,1)
Find the point where the line crosses the XY Plane.
View SolutionFind the Cartesian equation of the plane passing through the point (1,2,-3) perpendicular to the vector2i-j+2k .
View SolutionFind the Cartesian equation of the plane passing through the point (1,2,-3) perpendicular to the vector2i-j+2k .
Find the angle between the Plane and the line `(x-1)/2=(y-3)/3=z/6`
View SolutionFind the angle between the lines having direction ratios 1,1,2 and `sqrt3-1,-sqrt3-1,4`
View SolutionIf lines `(x-1)/3=(y-1)/(2lambda)=(z-3)/2` and `(x-1)/(3lambda)=(y-1)/1=(z-6)/-5` are perpendicular , find the value of `lambda`
View SolutionFind the equation of the plane passing through the points (3,-1,2) , (5,2,4) ,(-1,-1,6)
View SolutionFind the equation of the plane passing through the points (3,-1,2) , (5,2,4) ,(-1,-1,6) .Find the perpendicular distance from the point (6,5,9) to this plane.
View SolutionConsider the vector equation of two planes
`barr.(2i+j+k)=3,barr(i-j-k)=4`
Find vector equation of any plane through the intersection of the above two planes.
View SolutionConsider the vector equation of two planes `barr.(2i+j+k)=3,barr.(i-j-k)=4` Find vector equation of the plane through the intersection of the above planes and the point (1,2,-1).
View SolutionConsider the planes `2x+y-2z=5` and `3x-6y-2z=7`.Find their normal vectors.
View SolutionConsider the planes
`2x+y-2z=5` and
`3x-6y-2z=7`
Find the angle between these two planes.
View SolutionIf `a_1,b_1,c_1` and `a_2,b_2,c_2` are the direction ratios of two lines , then write the condition of its perpendicularity.
View SolutionFind the angle between the lines
`(x+3)/3=(y-1)/5=(z+3)/4` and
`(x+1)/1=(y-4)/1=(z-5)/2` .
View SolutionFind the shortest distance between the lines `barr=i+j+lambda(2i-j+k)` and `barr=2i+j-k+mu(3i-5j+2k)`
View SolutionThe equation of the line which passes through the point (1,2,3) and parallel to the vector 3i+2j-2k is
View SolutionFind the angle between the pair lines
`barr=2i-5j+k+lambda(3i+2j+6k)` and
`barr=7i-6k+mu(i+2j+2k)`
View Solution
EXAMPLE questions and complete solutions for chapter THREE DIMENSIONAL GEOMETRY of MAXIMUM PUBLICATION of Class 12