Complete Solutions to EXAMPLE of chapter LINEAR PROGRAMMING of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LINEAR PROGRAMMING |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 58 |
| Academic Year | 2023-24 |
Solve the following LPP Graphically,
Maximise, `Z=60x+15y`
Subject to constriants,
`x+yle50,3x+yle90,xge0,yge0`
View SolutionSolve the following LPP Graphically,
Minimise, `Z=-3x+4y`
Subject to constraints,
`x+2yle8, 3x+2yle12,xge0,yge0`
View SolutionSolve the following LPP Graphically,
Minimise, `Z=3x+5y`
Subject to constraints,
`x+3yge3, x+yge2,xge0,yge0`
View SolutionOne kind of cake requires 200g of flour and 25g of fat ,and another kind of cake requires 100g of flour and 50g of fat.Find the maximum number of cakes which can be made from 5kg of flour and 1kg of fat assuming that there is no shortage of the other ingredients,used in making the cake.
View SolutionA factory makes tennis rackets and bats,A tennis racket takes 1.5 hours of machine and 3 hours of craftsman's time in its making,while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time.In a day,the factory has availibilityof not more than 42 hours of machine time and 24 hours of craftman's time.
What no of rackets and bats must be produced if the factory is to work at full capacity?
View SolutionA factory makes tennis rackets and bats,A tennis racket takes 1.5 hours of machine and 3 hours of craftsman's time in its making,while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time.In a day,the factory has availibilityof not more than 42 hours of machine time and 24 hours of craftman's time.
if the profit on a racket and a bat isRs20 and Rs10 find maximum profit
View SolutionTwo godowns A and B have grains capacity of 100 quintals and 50 quintals respectively.They supply to 3 ration shop D,E,F whose requirement are 60,50 and 40 quintals respectively.The cost of transportation per quintal from the godowns to the shops is given in the following table,
transportation cost per quintal(in Rs).
Hence should the supplies be transported in order that the transportation cost is minimum?What is the minimum cost?

View SolutionChoose the correct answer from the bracket.If an LPP is consistent,then its feasible region is always
View SolutionMaximise` Z=2x+3y` subject to the
constraints x+y<4`,`x>0`,`y>0`
View SolutionThe graph of linear programing problem is given below.The shaded region is the feasible region.The objective function is
` Z=px+qy`
What are the co ordinates of the corners of the feasible region.
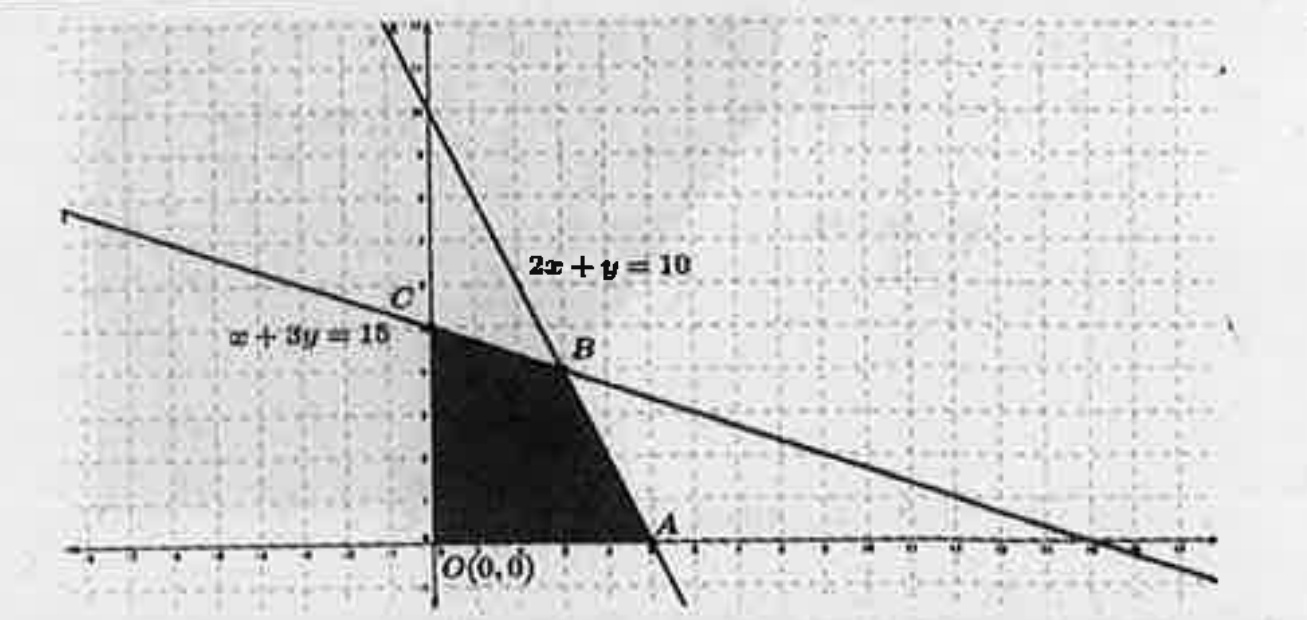
View SolutionThe graph of linear programing problem is given below.The shaded region is the feasible region.The objective function is
` Z=px+qy`
Write the constraints.
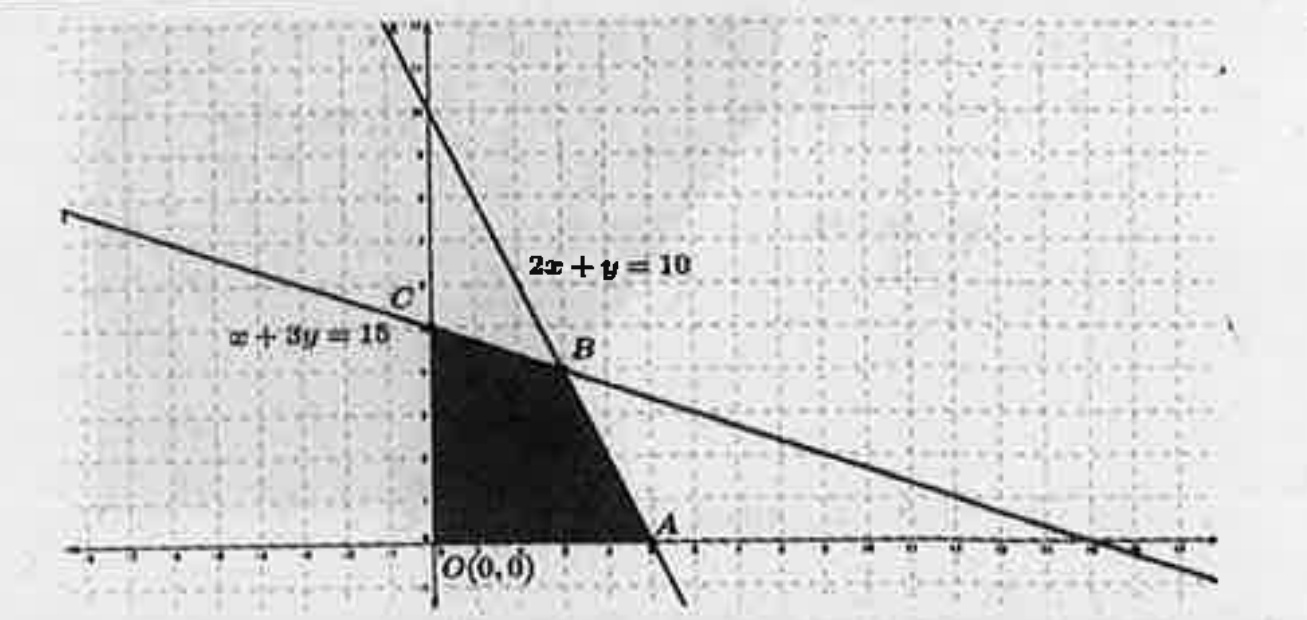
View SolutionThe graph of linear programing problem is given below.The shaded region is the feasible region.The objective function is
` Z=px+qy`
What are the co ordinates of the corners of the feasible region.

View SolutionThe graph of linear programing problem is given below.The shaded region is the feasible region.The objective function is
` Z=px+qy`
Write the constraints.

View SolutionThe graph of linear programing problem is given below.The shaded region is the feasible region.The objective function is
`Z=3x+2y`
Find the Max Z.
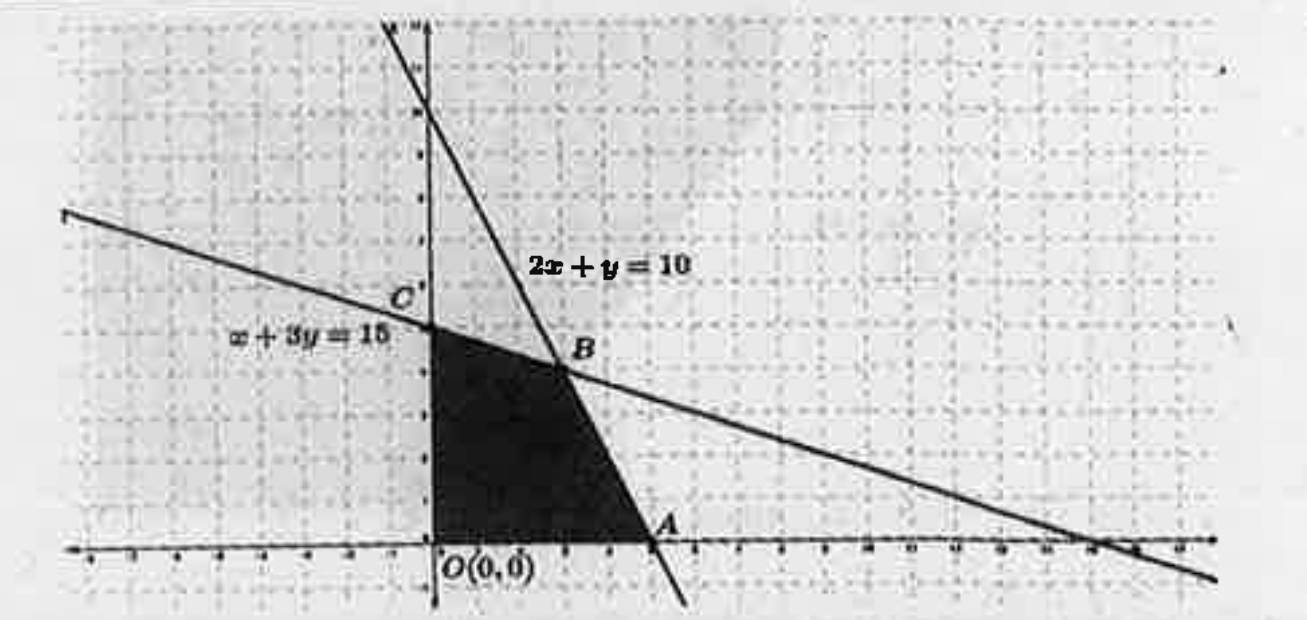
View SolutionA diet is to contain atleast 80 units of vitamin A and 100 units of minerals.Two foods F1 and F2 are available.Food F1 costs Rs 4 per unit food and F2 costs Rs 6 per unit.One unit of food F1 contains 3 units of vitamin A and 4 units of minerals.One unit of food F2 contains 6 unit of of vitamin A and 3 units of minerals.Formulate this as a linear programming problem.Find the minimum costs for diet that consists of misture of these two foods and also meets the minimal nutritional requirements.
View SolutionConsider the linear programming problem,
Maximise, `Z=x+y`,`2x+y-3le0`,`x-2y+1le0`,`yle3`,`xge0`,`yge0`
Draw its feasible region.
View SolutionConsider the linear programming problem,
Maximize, `Z=x+y`, subject to constraints `2x+y-3le0`,`x-2y+1le0`,`yle3`,`xge0`,`yge0`
Find the corner points of the feasible region.
View SolutionConsider the linear programming problem,
Maximise, `Z=x+y`, subject to the constraints `2x+y-3le0`,`x-2y+1le0`,`yle3`,`xge0`,`yge0`
Find the corner at which Z attains its maximum.
View SolutionConsider the LPP
Minimise,Z=200x+500y
`x+2yge10`,`3x+4yle24`,`xge0`,`yge0`
Draw the feasible region.
View SolutionConsider the LPP
Minimise,Z=200x+500y
`x+2yge10`,`3x+4yle24`,`xge0`,`yge0`
Find the co-ordinates of the corner points of the feasible region.
View SolutionConsider the LPP
Minimize,Z=200x+500y
`x+2yge10`,`3x+4yle24`,`xge0`,`yge0`
Solve the LPP.
View SolutionConsider the LPP
Maximise, `Z=5x+3y`
Subject to,`3x+5yle15`,`5x+2yle10`,`x,yge0`
Draw the feasible region.
View SolutionConsider the LPP
Maximise, `Z=5x+3y`
Subject to,`3x+5yle15`,`5x+2yle10`,`x,yge0`
Find the corner points of the feasible region.
View SolutionConsider the LPP
Maximise, `Z=5x+3y`
Subject to,`3x+5yle15`,`5x+2yle10`,`x,yge0`
Find the corner at which Z attains its maximum.
View SolutionConsider the linear programming problem:
Minimise `Z=3x+9y`
subject to the constraints:
`x+3yle60 x+yge10`,`xley`,`xge0`,`yge0`.
Draw its feasible region.
View SolutionConsider the linear programming problem:
Minimise `Z=3x+9y`
subject to the constraints:
`x+3yle60 x+yge10`,`xley`,`xge0`,`yge0`.
Find the vertics of the feasible region.
View SolutionConsider the linear programming problem:
Minimise `Z=3x+9y`
subject to the constraints:
`x+3yle60, x+yge10`,`xley`,`xge0`,`yge0`.
Find the minimum value of Z subject to the given constraints.
View SolutionConsider the linear inequalities
`2x+3yle6`,`2x+yle4`,`x,yge0`
Mark the feasible region.
View SolutionConsider the linear inequalities
`2x+3yle6`,`2x+yle4`,`x,yge0`
Maximise the function `z=4x+5y` subject to the given constraints.
View SolutionConsider the linear programming problem:
Minimise `Z=-3x+4y`
Subject to `x+2yle8`,`3x+2yle12`,x,y >.0 Mark its feasible region.
View SolutionConsider the linear programming problem:
Minimise `Z=-3x+4y`
Subject to `x+2yle8`,`3x+2yle12`,x,y`ge`0`
Find the corner points of the feasible region.
View SolutionConsider the linear programming problem:
Minimise `Z=-3x+4y`
Subject to `x+2yle8`,`3x+2yle12`,x,y`ge`0`
Find the corner at which Z attain its minimum.
View SolutionConsider the linear programming problem:
Maximize `z=4x+y`
Subject to constraints:
`x+yle50`,`3x+yle90`,`x,yge0`
Draw the feasible region.
View SolutionConsider the linear programming problem:
Maximize `z=4x+y`
Subject to constrains:
`x+yle50`,`3x+yle90`,`x,yge0`
Find the corner at which 'z' attains its maximum value.
View SolutionConsider the linear programming problem:
Maximize `z=4x+y`
Subject to constrains:
`x+yle50`,`3x+yle90`,`x,yge0`
Find the corner at which 'z' attains its maximum value.
View SolutionConsider the LPP
Maximise `z=3x+2y`
Subject to the constraints
`x+2yle10`,3x+y`le`15`,`x,y`ge`0`
Find the corner points of the feasible region.
View SolutionConsider the LPP
Maximise `z=3x+2y`
Subject to the constraints
`x+2yle10`,3x+y`le`15`,`x,y`ge`0`
Find the corner points of the feasible region.
View SolutionConsider the LPP
Maximise `z=3x+2y`
Subject to the constraints
`x+2yle10`,3x+y`le`15`,`x,y`ge`0`
Find the maximum value of Z.
View SolutionConsider the linear programming problem:
Maximum `z=50x+40y`
subject to constraints:
`x+2yle10`,`3x+4yge24`,`x,yge0`
Draw the feasible region.
View SolutionConsider the linear programming problem:
Maximum `z=50x+40y`
subject to constraints:
`x+2yle10`,`3x+4yge24`,`x,yge0`
Find the corner points of the feasible region.
View SolutionConsider the linear programming problem:
Maximum `z=50x+40y`
subject to constraints:
`x+2yle10`,`3x+4yge24`,`x,yge0`
Find the maximum value of z.
View SolutionA furniture dealer sells only tables and chairs.He has Rs.12,000 to invest and a space to store 90 pieces.A table costs him Rs.400 and a chair Rs.100. He can sell a table at a profit of Rs.75 and a chair at a profit of Rs.25. Assume that he can sell all the items.The dealer wants to get maximum profit.By defining suitable variables ,write the objective function.
View SolutionA furniture dealer sells only tables and chairs.He has Rs.12,000 to invest and a space to store 90 pieces.A table costs him Rs.400 and a chair Rs.100. He can sell a table at a profit of Rs.75 and a chair at a profit of Rs.25. Assume that he can sell all the items.The dealer wants to get maximum profit.Write the constraints.
View SolutionA furniture dealer sells only tables and chairs.He has Rs.12,000 to invest and a space to store 90 pieces.A table costs him Rs.400 and a chair Rs.100. He can sell a table at a profit of Rs.75 and a chair at a profit of Rs.25. Assume that he can sell all the items.The dealer wants to get maximum profit.
Maximise the objective function graphically.
View SolutionA company produces two types of cricket balls A and B.The production time of one ball of type B is double the type A(time in units ).The company has the time to produce a maximum of 2000 balls per day. The supply of raw materials is sufficient for the production of 1500 balls (both A and B) per day. The company wants to make maximum profit by making profit of Rs.3 from a ball type of A and Rs.5 from type B. Then,
By defining suitable variables write the objective function.
View SolutionA company produces two types of cricket balls A and B.The production time of one ball of type B is double the type A(time in units ).The company has the time to produce a maximum of 2000 balls per day.The supply of raw materials is sufficient for the production of 1500 balls (both A and B) per day.The company wants to make maximum profit by making profit of Rs.3 from a ball type of A and Rs.5 from type B.Then,
Write the constraints.
View SolutionA company produces two types of cricket balls A and B.The production time of one ball of type B is double the type A(time in units ).The company has the time to produce a maximum of 2000 balls per day.The supply of raw materials is sufficient for the production of 1500 balls (both A and B) per day.The company wants to make maximum profit by making profit of Rs.3 from a ball type of A and Rs.5 from type B.Then,
How many balls should be produced in each type per day in order to get maximum profit?
View SolutionThe graph of linear programing problem is given below.The shaded region is the feasible region.The objective function is
` Z=px+qy`
What are the co ordinates of the corners of the feasible region.

View SolutionThe graph of linear programing problem is given below.The shaded region is the feasible region.The objective function is
` Z=px+qy`
Write the constraints.

View SolutionThe graph of linear programming problem is given below.The shaded region is the feasible region.The objective function is Maximise, `Z =px+qy`
` If the Max,Z occurs at A and B,what is the relation between pand q?
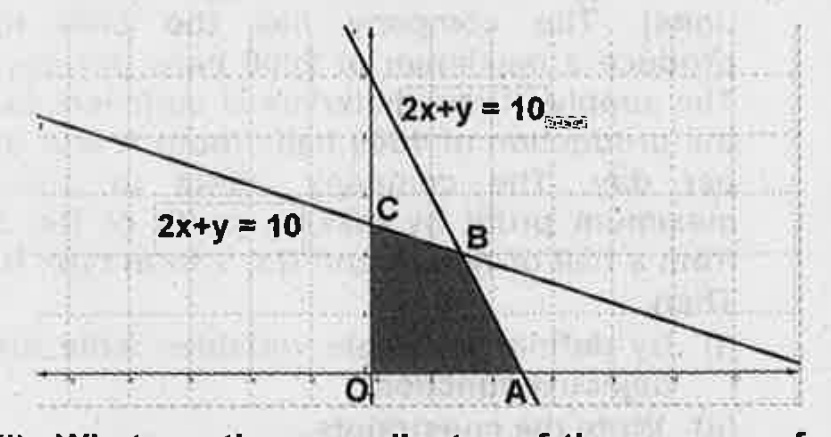
View SolutionThe graph of linear programming problem is given below.The shaded region is the feasible region.The objective function is Maximise, `Z =px+qy`
If q=1, write the objective function when maximum of Z occures at A and B.`
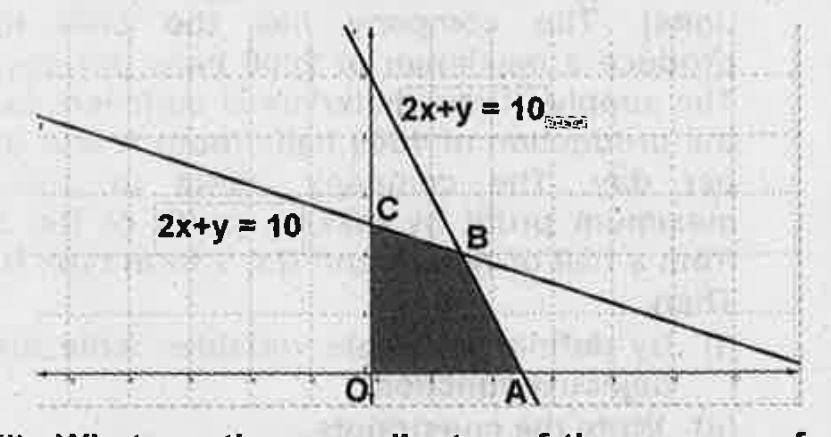
View SolutionThe graph of linear programing problem is given below.The shaded region is the feasible region.The objective function is
`Z=3x+2y`
Find the Max Z.

View SolutionA manufacturur produces nuts and bolts.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts.He earns a profit of Rs.17.50 per package on nuts and Rs.7 per package on bolts.How many package of each should be produced each day so as to maximise the profit,if he operates his machine for at the most 12 hours a days?
By suitable defining the variables write the objective function of the problem.
View SolutionA manufacturur produces nuts and bolts.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts.He earns a profit of Rs.17.50 per package on nuts and Rs.7 per package on bolts.How many package of each should be produced each day so as to maximise the profit,if he operates his machine for at the most 12 hours a days?
Formulate the problem as a linear programming problem.
View SolutionA manufacturur produces nuts and bolts.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts.He earns a profit of Rs.17.50 per package on nuts and Rs.7 per package on bolts.How many package of each should be produced each day so as to maximise the profit,if he operates his machine for at the most 12 hours a days?
Solve the LPP graphically and find the number of packages of nuts and bolts to be manufactured.
View SolutionA bakery owner makes two types of cakes A and B. Three machines are needed for this purpose.The time (in minutes) requried for making each type of cake in each of the machines is given below:
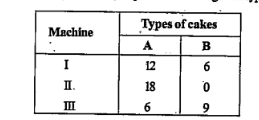
Each machine is available for atmost 6 hours per day. Assume that all cakes will be sold out every day.The bakery owner wants to make maximum profit per day by making 7.50 from type A and 5 from type B.
write the object function
View SolutionA bakery owner makes two types of cakes A and B.There machines are needed for this purpose.The time(in minutes) required for making each type of cakes in each machine is given below,
Each machine is available for atmost 6 hours per day.Assume that all cakes will be sold out everyday.The bakery owner wants to make maximum profit per day by making Rs.7.5 from type A and Rs.5 from type B.
Find the maximum profit graphically.
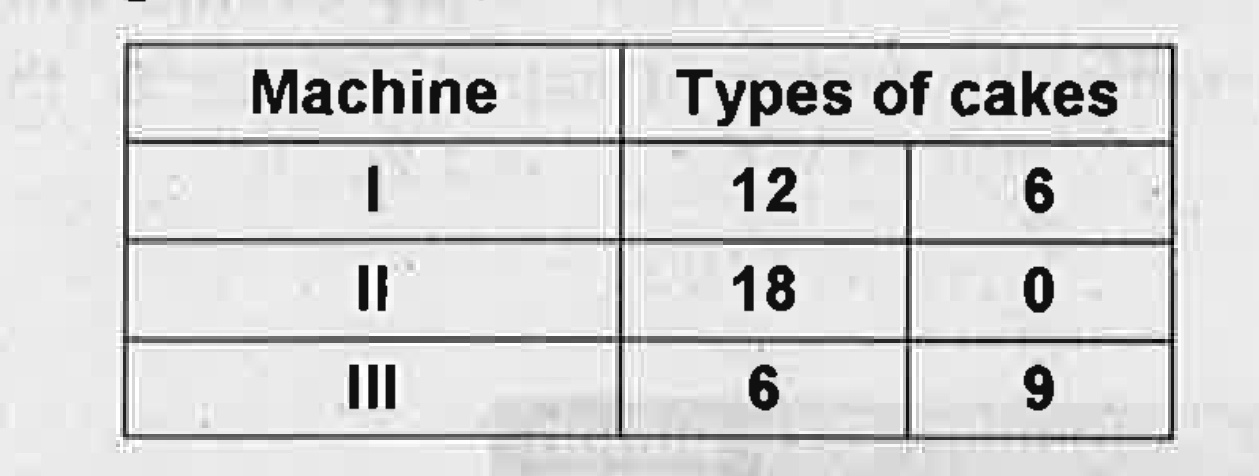
View SolutionIn factory there are two machines A and B producing toys.They respectively produce 60 and 80 units in one hour.A can run a maximum of 10 hours and B a maximum of 7 hours a day .The cost of their running per hour respectively amount to 2,000 and 2,500 rupee.The total duration of working these machines cannot exceed 12 hours a day.If the total cost cannot exceed Rs. 25,000 per day and the total daily production is atleast 800 units,then formulate the problem mathematically.
View Solution
EXAMPLE questions and complete solutions for chapter LINEAR PROGRAMMING of MAXIMUM PUBLICATION of Class 12