Complete Solutions to EXAMPLE of chapter MODEL QUESTION of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MODEL QUESTION |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Let R be a relation on the set {1,2,3}
given by `R={(1,1),(2,2),(1,2),(2,1),
(2,3)}`.Which among the following
element to be included to R so that R
becomes Symmetric?
View SolutionIf * is defined by `a`*`b=a-b^2` and `oplus`
is defined by `a oplus b`=`a^2+b`,where `a
and b` are integers.Then find the value
of `(`3`oplus`4`)`*`5`
View SolutionIf `X+Y=[[5,2],[0,9]]` and `X-Y=[[3,6],[0,-1]],
`f``i``nd` ` ` `2X-3Y`.
View SolutionFind rate of Change of area of a circle
with respect to the radius,when r=10cm
View SolutionFind rate of change of area of a circle with respect to the time when the radius is increasing at the rate 0.7 cm/s.Given that `r=5cm`
View SolutionIntegrate `int (1+logx)^2/xdx`
View Solutionint `(f'(x))/f(x)dx`=…….. a)`[f(x)]^2/2+c` b)`logabs[f(x)]+c` c)`logabs[[f'(x)]/[f(x)]]+c`
d)`logabs[f'(x)]+c`
View SolutionFind the area of a circle with centre (0,0)
and radius 'a' using integration.
View SolutionConsider the differential equation
`dy/dx=(x+y)/x`
Write the order of the differential
equation.
View SolutionConsider the differential equation `dy/dx=(x+y)/x`
Solve the above given differential equation.
View SolutionFollowing table shows a brief description
about manufacturing process of a
company.Time required in hours per unit
of the product and maximum availability
of machine is also given in the table:
Write the constraints.

View SolutionA function `f:ArarrB`,where `A={1,2,3}` and `B={4,5,6}` defined by `f(1)=5`,`f(2)= 6`,`f(3)=4`,Check whether f is a bijection.If it is a bijection,Write `f^-1` as set of ordered pair.
View SolutionThe operation table for an operation `ast` is
given below.Given that 1 is the identity
element.Then which among the
following is true regarding the element in
the first column?
Check whether `ast` is commutative.

View SolutionIf `sin^-1x=y`,then
View SolutionWrite the principal value of `sin^-1(frac(1)(2))`
View SolutionIf `sin^-1x=pi/4`,find the value of `cos^-1x`
View SolutionFind the relation between 'a' and 'b' if the function `f` defined by
`f(x)={(ax+1,xle3),(bx+3,x>3):}` is continuous.
View Solution"All continuous function are not
differentiable." Justify your answer
with an example
View SolutionFind the equation to the tangent to the
curve `y=x^2-2x+7` at (2,7)
View SolutionIntegrate `int(x+2)/(2x^2+6x+5)dx`
View SolutionConsider the differential equation
`xdy/dx+y=1/x^2`
Find the integrating factor.
View SolutionSolve the differential equation `xdy/dx+y=1/x^2`.
View SolutionIf the vectors `vec(PQ)=-3i+4j+4k` and `vec(PR)=-5i+2j+4k` are the sides of a `trianglePQR` Find the angle between `vec(PQ)` and `vec(PR)`
View SolutionIf the vectors `vec(PQ)=-3i+4j+4k` and `vec(PR)=-5i+2j+4k` are the sides of a `trianglePQR`.Find the length of the median through the vertex P.
View SolutionIf `veca=5i-j-3k` and `vecb=i+3j+5k`,then show that the vectors `veca+vecb`,`veca-vecb` are perpendicular.
View SolutionIf `veca=i-2j+3k`,`vecb=2i+3j-4k` and `vecc=i-3j+5k`,then check whether `veca`,`vecb`,`vecc` are coplanar.
View SolutionFind the Cartesian equation of the line passing through origin and (5,-2,3)
View SolutionThe point P(x,y,z) lies in the first octant and its distance from the origin is 12 units.If the position vector of P makes angles 45°,60° with x and y axes respectively,find coordinates of P.
View SolutionSolve graphically.
Maximise `Z=5x+3y`
Subject to the constraints
`3x+5yle15`,`5x+2yle10`,`xge0`,`yge0`
View Solution`A=[[3,3,-1],[-2,-2,1],[-4,-5,2]]` Find `A^T`
View SolutionExpress the following matrices as the sum of a Symmetric and a Skew Symmetric matrix.
`[[3,3,-1],[-2,-2,1],[-4,-5,2]]`
View SolutionIf `A^T=[[cosx,sinx],[-sinx,cosx]]`,Verify that `A^TA=I`
View SolutionWithout expanding prove that
`abs[[x+y,y+z,z+x],[z,x,y],[1,1,1]]=0`
View SolutionConsider the following system of equations `2x-3y+5z=11`, `3x+2y-4z=-5`,`x+y-2z=-3` Express the system in `Ax=B` form.
View SolutionConsider the following system of
equations
`2x-3y+5z=11`,`3x+2y-4z=-5`,`x+y-2z=-3`
Solve the system by matrix method.
View SolutionFind `dy/dx` of the following
`x^2+xy+y=100`
View SolutionFind dy/dx of the following `y^x=2^x`
View SolutionFind dy/dx of the following
`x=costheta`,`y=sintheta` at `theta=pi/4`
View SolutionEvaluate the integrals
`intx/((x+1)(x+2))dx`
View SolutionEvaluate the following `int_0^1 xe^(x^2)dx`
View SolutionEvaluate the following `int_-5^5 abs[x+2]dx`
View SolutionConsider the parabolas `y^2=4x`,`x^2=4y` Draw a rough figure for the above parabolas.
View SolutionConsider the parabolas `y^2=4x`,`x^2=4y`
Find the point of intersection of the
two parabolas.
View SolutionConsider the parabolas `y^2=4x`,`x^2=4y`
Find the area bounded by these two
parabolas.
View SolutionFind the shortest distance between the
lines whose vector equations are
`vecr=(i+2j+3k)+lambda(i-3j+2k)` and
`vecr=(4i+5j+6k)+mu(i-3j+2k)`
View Solution(i) If a plane meets positive x axis at a
distance of 2units from the origin,
positive y axis at a distance of 3 units
from the origin and positive z axis at a
distance of 4 units from the origin.
Find the equation of the plane.
(ii) Find the perpendicular distance of (0,0,0)
from the plane obtained in part (i)
View SolutionA die is thrown twice let the event A be 'odd number on first throw' and B be 'odd number on the second throw' check whether A and B are independent.
View SolutionIf ` ` `f(x)=x/(x-1)` ,`x!=1`
Find fof(x)
View Solutionif `f(x)=x/(x-1)` ,`x!=1`find the inverse of f
View SolutionUsing elementary row operations, find the inverse of the matrix
`[[1,2],[2,-1]]`
View Solutionf(x) is a strictly increasing function, if f'(x) is........a)Positive b)Negative c)0 d)None of these
View SolutionShow that the function F given by
`f(x)=x^3-3x^2+4x,x in R`
is strictly increasing
View Solution`int_0^af(a-x)dx` =..... a)`int_0^(2a)f(x)dx` b)`int_-a^af(x)dx` c)`int_0^af(x)dx`
d)`int_a^0f(x)dx`
View SolutionFind the value of
`int_0^(pi/2)sin^4x/(sin^4x+cos^4x)dx`
View SolutionFind the area of the region bounded by the curve
`y^2=x`
x-axis and the lines x=1 and x=4
View SolutionFind the general solution of the differential equation
`xdy/dx+2y=x^2 log x`
View SolutionA manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns profit of Rs. 17.50 per package on nuts and Rs. 7.00 per package on bolts. Formulate the above LPP if the machine operates for at most 12 hours a day
View SolutionLet
`A=NtimesN` and `ast`
be a binary operation on A defined by (a,b)*(c,d) = (a + c,b + d)
Find (1,2)*(2,3)
View SolutionLet
`A=NtimesN` and `ast`
be a binary operation on A defined by (a,b)*(c,d) = (a + c,b + d)
Prove that
`ast`
is commutative
View SolutionLet
`A=NtimesN` and `ast`
be a binary operation on A defined by (a,b)*(c,d) = (a + c,b + d)
Prove that
`ast`
is associative
View SolutionIdentify the function from the above graph
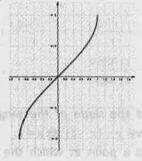
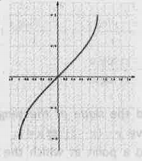
View SolutionFind the domain and range of the function represented in above graph
View SolutionProve that
`tan^-1 (1/2)+tan^-1(2/11)=tan^-1(3/4)`
View Solution`(d(a^x))/dx` =... a)`a^x` b)`log(a^x)` c)`a^xlog a` d)`xa^(x-1)`
View SolutionFind `dy/dx` if `x^y` = `y^x`
View SolutionFind the slope of the tangent to the curve `y=(x-2)^2` at x=1
View SolutionFind a point at which the tangent to the curve `y=(x-2)^2` is parallel to the chord joining the point A (2,0) and B(4,4)
View SolutionEvaluate `int_0^2(x^2+1)dx`
as the limit of a sum
View SolutionConsider the following figure
Find the point of intersection 'P' of the circle
`x^2+y^2 = 50`
and the line y = x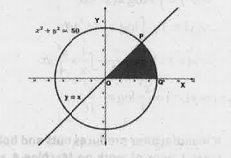
View SolutionThe degree of the differential equation
`xy((d^2y)/dx^2)^2+x^4(dy/dx)^3-ydy/dx=0` is
View SolutionFind the general solution of the differential equation
`sec^2xtan ydx +sec^2 y tan xdy=0`
View SolutionProve that for any vector
`bar a,barb,barc[bara+barb, barb+barc, barc+bara]=2[bara barb barc]`
View SolutionShow that if
`bara+barb,barb+barc,barc+bara`
are coplanar then
`bara,barb,barc` are also coplanar
View SolutionFind the equation of a plane which makes x,y,z intercepts respectively as 1,2,3
View SolutionSolve the following LPP Graphically,
Minimise, `Z=-3x+4y`
Subject to constraints,
`x+2yle8, 3x+2yle12,xge0,yge0`
View SolutionFind x and y if
`x[[2],[3]]+y[[-1],[1]]=[[10],[5]]`
View SolutionExpress the matrix
`[[2,-2,-4],[-1,3,4],[1,-2,-3]]`
as the sum of a symmetric and a skew symmetric matrices.
View Solutionprove that `abs[[a,b,c],[a+2x,b+2y,c+2z],[x,y,z]]=0`
View Solutionif `A=[[1,-1,2],[0,2,-3],[3,-2,4]]` `B=[[-2,0,1],[9,2,-3],[6,1,-2]]` Prove that `B=A^-1`
View Solutionif
`A=[[1,-1,2],[0,2,-3],[3,-2,4]]` `B=[[-2,0,1],[9,2,-3],[6,1,-2]]`
Using
`A^-1` solve the system of linear equation given below: x-y+2z=1, 2y-3z=1, 3x-2y+4z=2
View SolutionProve that the function defined by
`f(x)= cosx^2`
is a continuous function
View Solutionif
`y=e^(a cos^-1x),-1lexle1`, show that
`dy/dx= (-ae^(acos^-1x))/(sqrt(1-x^2))`
View SolutionEvaluate `int sin mxdx`
View SolutionEvaluate `int 1/(sqrt (x^2+2x+2))dx`
View SolutionEvaluate `int x/((x+1)(x+2))dx`
View Solutionif `bara=3i+2j+2k,barb=i+2j-2k` find `bara+barb,bara-barb`
View Solutionif `bara=3i+2j+2k,barb=i+2j-2k` find a unit vector perpendicular to both `bara+barb,bara-barb`
View SolutionConsider the points A(1.2.7),B(2,6,3),C(3,10,-1)
find `bar(AB),bar(BC)`
View SolutionConsider the points A(1,2,7),B(2,6,3),C(3,10,-1)
prove that A,B,C are collinear points
View SolutionFind the angles between the lines
`(x-2)/2=(y-1)/5=(z+3)/-3` and `(x+2)/-1=(y-4)/8=(z-5)/4`
View Solutionfind the shortest distance between the pair of lines
`barr=(i+2j+3k)+lambda(i-3j-2k)` `barr=(4i+5j+6k)+mu(2i+3j+k)`
View SolutionThe probability distribution of a random variable is given by p(x) . What is `sumP(x)` ?
View SolutionThe following is a probability distribution function of a random variable
Find K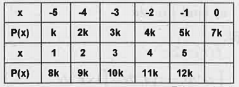
View SolutionConstruct a `2times2` matrix whose elements are given `a_(ij)=2i+j`
View SolutionConstruct a `2times2` matrix whose elements are given `a_(ij)=2i+j`.find `A^2`
View SolutionIf `intf(x)/(x^2+1)dx=logabs(x^2+1)+C`, then
`f(x)`=……………..
View SolutionFind `intxe^xdx`
View SolutionForm the differential equation of the family of all circles touching the y-axis at origin.
View SolutionConsider the relation in the set N of natural numbers defined as `R={(a,b):ab` is a factor of 6}. Determine whether the relation is reflexive, symmetric or transitive.
View SolutionFind the area bounded by the curve `y=cosx` and x axis between `x=0` and `x=pi`.
View Solution
EXAMPLE questions and complete solutions for chapter MODEL QUESTION of MAXIMUM PUBLICATION of Class 12