Complete Solutions to Exercise ( Level 1 (single correct answer type questions)) of chapter QUADRATIC EQUATIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | QUADRATIC EQUATIONS |
| MCGROW HILL PUBLICATION | Exercise ( Level 1 (single correct answer type questions)) |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
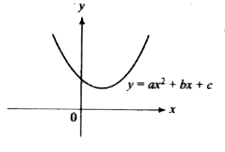
If fig. 3.21 graph of `y = ax^(2) + 2bx + c` is given Which one of the following is not true ?
View SolutionIf `ax^(2) + 2bx + c = 0 and ax^(2) + 2cx + b = 0, b ne c` have a common root, then `(a + b + c)/( a)` is equal to
View SolutionSuppose `a,b,c in R ` `a ne 0 `and `4a - 6b +9c lt 0`. if ` ax^(2) + bx + c = 0` does not have real roots, then `(b + c)/( a)` is less than
View SolutionIf `alpha, beta` be the roots of `4x^(8) - 16x + c = 0, c in R` such that `1 lt alpha lt 2 and 2 lt beta lt 3`, then the number of integral values of c is
View SolutionIf equations `x^2+a x+12=0. x^2+b x+15=0a n dx^2+(a+b)x+36=0,` have a common positive root, then find the values of `aa n dbdot`
View SolutionSuppose `a, b in R`. If the equation `(a)/(x) = (1)/( x - b) + (1)/( x + b) ` is not satisfied by any real value of x, then
View SolutionSuppose `a in R, a ne - 1//2 . " Let " alpha, beta` be roots of `(2a + 1) x^(2) - ax + a - 2 = 0 If alpha lt 1 lt beta `, then
View SolutionSuppose `alpha, beta` are roots of `8x^(2) - 10 x + 3 = 0` , then `sum_(n=0) ^(infty) (alpha^(n) + beta^(n))` is
View SolutionSuppose `a, b, c in R, a ne 0. If a + |b| + 2c = 0`, then roots of `ax^(2) + bx + c = 0` are
View SolutionSuppose `0 lt b lt c and f(x) = (x^(2) - bc)/( 2x - (b + c)) , x in R`, then f(x) cannot lie in
View SolutionIf ` alpha and beta ` are the roots of ` x^(2) +px+q=0` and ` gamma , delta `are the roots of ` x^(2) +rx+x=0` , then evaluate `(alpha - gamma ) ( beta - gamma ) (alpha - delta ) ( beta - delta) ` in terms of p,q,r and s .
View Solution[ The number of real solutions of x^(2)-4|x|-2=0 is [ (a) 1, (b) 2 (c) 3, (d) 4]]
View SolutionThe number of real solutions of `x^(2) - 3|x| + 2 = 0` is
View SolutionIf `2 + sqrt(5)` is root of `x^(2) - px + q = 0 ` where p and q are real, then the ordered pair (p,q) is equal to
View SolutionIf the quadratic equation `2x(2) - px + q = 0 ` where p and q are real, then the ordered pair (p,q) is equal to
View Solutionif a,b, c, d and p are distinct real number such that
`(a^(2) + b^(2) + c^(2))p^(2) - 2p (ab + bc + cd) + (b^(2) + c^(2) + d^(2)) lt 0` then a, b, c, d are in
View SolutionThe number of values of `a` for which equations `x^3+a x+1=0a n dx 64+a x^2+1=-` have a common root is `0` b. `1` c. `2` d. Infinite
View SolutionThe number of values of `a` for which equations `x^3+a x+1=0a n dx 64+a x^2+1=-` have a common root is `0` b. `1` c. `2` d. Infinite
View SolutionThe roots of the equation `|x^2-x-6|=x+2` are
View SolutionThe number of real roots of the equation `|x|^(2) -3|x| + 2 = 0`, is
View SolutionThe least value of `n in N` for which `(n - 4)x^(2) + 8x + n + 2 gt 0 AA x in R`, is
View SolutionLet f(x) be a quadratic expression such that `f(x) lt 0 AA x in R` . If g(x) f'(x) + f''(x) then for `x in R`.
View SolutionIf x + 1 is a factor of `x^(4) + (p - 3) x^(3) - (3p - 5) x^(2) + (2p - 9) x + 12` , then value of p is
View SolutionIf both the roots of the equation are negative `x^2-(p-4)x+2e^(2lnp)-4=0` then p belongs to
View Solution[ Let f and g be two real valued functions and S={x|f(x)=0} and T={x|g(x)=0}, then S nn T represent the set of roots of [ (a) f(x)g(x)=0, (b) f(x)^(2)+g(x)^(2)=0 (c) f(x)+g(x)=0, (d) (f(x))/(g(x))=0]]
View Solution[ If domain of f(x)=sqrt(x^(2)+bx+4) is R, then maxi- mum possible integral value of b is [ (a) 2, (b) 3 (c) 4, (d) 5]]
View SolutionIf `p in (-1, 1)` , then roots of the quadratic equation `(p - 1)x^(2) + px + sqrt(1 - p^(2)) = 0` are
View SolutionIf a,b,c are positive real numbers, then the number of positive real roots of the equation `ax^(2)+bx+c=0` is
View SolutionIf the roots of the equation `x^(2) + p^(2) = 8x + 6p` are real, then p belongs to be interval
View SolutionIf the sum of the roots of the equation `(a+1)x^2=(2a+3)x+(3a+4)=0` is -1, then find the product of the roots.
View SolutionIf 3 - 4i is a root of `x^(2) - px + q = 0 ` where p, q `in R`. then value `(2 p - q)/( p + q)` is
View SolutionIf x = 1 + i is a root of `x^(3) - ix + 1 - i = 0` , then the quadratic equation whose roots are the remain - ing two roots of `x^(3) - ix + 1 - i = 0` is
View SolutionIf `alpha and beta ` be the roots of the eqution `x^(2) +px -1/ (2p^(2)) = 0`, where p `in R`. Then the minimum possible value of `alpha^(2) + beta^(2)` is
View SolutionThe equation `sqrt(x+3-4sqrt(x-1))+sqrt(x+8-6sqrt(x-1))=` hs
View SolutionThe equation `[ x - x^(2) - 1| = |2 x - 3 - x^(2) ]` has
View SolutionIf sin `alpha, cos alpha` are the roots of the equation `ax^(2) + bx + c = 0, (a ne 0)` , then
View SolutionIf `x` is real and `k=(x^2-x+1)/(x_2+x+1)` , then `k in [1//3,3]` (b) `kgeq3` (c) `klt=1//3` (d) none of these
View SolutionIf the equation `x^(2) + bx + ca = 0 and x^(2) + cx + ab = 0` have a common root and `b ne c` , then their other roots will satisfy the equation
View SolutionIf the inequality `(m x^2+3x+4+2x)//(x^2+2x+2)<5` is satisfied for all `x in R ,` then find the value of `mdot`
View SolutionSuppose, a, b, c are three distinct real numbers. Let P (x) =`((x-b)(x-c))/((a-b)(a-c))+((x-c)(x-a))/((b-c)(b-a))+((x-a)(x-b))/((c-a)(c-b))`.
When simplified, P (x) becomes
View SolutionIf `ax^(2) + bx + c, a, b, c in R, a ne 0` has real zero and `a - b + c lt 0` , then value of ac is
View SolutionIf `alpha, beta` are the roots of the equation `x^(2)-2x-a^(2)+1=0` and `gamma, delta` are the roots of the equation
`x^(2)-2(a+1)x+a(a-1)=0` such that `alpha, beta epsilonn (gamma, delta)` find the value of `a`.
View SolutionIf ` alpha, beta` are the roots of the equation ` ax^(2) +2bx +c =0 and alpha +h, beta + h` are the roots of the equation ` Ax^(2) +2Bx + C=0` then
View SolutionThe quadratic equation `x^(2) + 7x = 14 (q^(2) + 1)` , where q is an integer has
View SolutionLet a,b,c ` in R and a gt 0`. If the quadratic equation ` ax^(2) +bx +c=0` has two real roots `alpha and beta` such that ` alpha gt -1 and beta gt 1` , then show that ` 1 + |b/a| + c/a gt 0`
View SolutionLet ` a,b,c in R and a ne 0` be such that ` (a + c)^(2) lt b^(2) ` ,then the quadratic equation ` ax^(2) + bx +c =0` has
View SolutionThe integral values of a for which the quadratic equation `(x - a) (x - 10) + 1 = 0` has integeral roots are
View SolutionThe number of real solution fo `4^(x + 1.5) + 9^(x + 0.5) = (10)/ (6^(x))` is
View SolutionNumber of solutions to the equation `2^(sin^2 x) +5.2^(cos^2 x) = 7,` in the interval `[-pi,pi],` is
View SolutionThe number of values of k for which the equation `x^(2) - 2x + k = 0` has two distinct roots lying in the interval (0,1) is
View SolutionIf roots of the equation `ax^2 + bx + c = 0` are `alpha/(alpha-1)` and `(alpha+1)/alpha` and then `(a+b+c)^2` equals
View SolutionLet `x` be an integer and `x^2 + x + 1` is divisible by 3. When is `x` divided by 3. it leaves remainder
View SolutionIf `alpha, beta` are roots of the equation `x^(2) + ax + b = 0`, then maximum value of `- x^(2) + ax + b + (1)/(4) (alpha - beta )^(2) ` is
View SolutionIf both the roots of the equation `x^(2) + bx + c = 0` lie in the interval (0,1) , then
View SolutionLet a, b, c `in R ` be such that a + b + c `lt 0, a - b + c lt 0 and c gt 0`. If `alpha and beta` are roots of the equation `ax^(2) + bx + c = 0 ` , then value of `[alpha] + [beta]` is
View SolutionFind the valuesof `m` for which exactly one root of the equation `x^(2)-2mx+m^(2)-1=0` lies in the interval `(-2,4)`
View SolutionThe value of `sqrt(8 + 2 sqrt(8 + 2 sqrt(8 + 2 sqrt(8 + . . . . )))) ` is
View SolutionThe number of solutions of the equation `sin((pix)/(2sqrt3))=x^2-2sqrt3x+4`
View SolutionThe number of solutions of `|x+2| = 2(3 - x) ` is
View SolutionIf the equation `ax^(2)+bx+c=0 (a lt 0)` has two roots `alpha` and `beta` such that `alpha lt -3` and `beta gt 3`, then
View SolutionTwo non-integer roots of `(x^(2) - 5x)^(2) - 7 (x^(2) - 5x) + 6 = 0` are
View SolutionThe number of real roots of `((x - 1)/( x + 1))^(4) - 13 ((x - 1)/( x + 1))^(2) + 36 = 0, x ne - 1` is
View SolutionThe number of negative roots of `9^(x +2) - 6 (3^(x +1)) + 1 = 0` is
View SolutionThe number of roots of `81 ((2x - 5)/( 3x +1))^(4) - 45 ((2x - 5)/(3x + 1))^(2) + 4 = 0 , x ne 1//3` is
View Solution`(x^2+3x+2)^2 - 8(x^2+3x) -4 =0`
View SolutionThe number of roots of the equation `sqrt((x)/(x - 3)) + sqrt((x - 3)/( x)) = (5)/(2), x ne 0, x ne 3 ` is
View Solution`4(x-1/x)^2+8(x+1/x)=29` is
View SolutionIrrational roots of the equaiton `2x^(4) + 9x^(3) + 8x^(2) + 9x + 2 = 0` are
View SolutionSum of the roots of the equaiton ` 4 (x - (1)/(x))^(2) - 4 (x - (1)/(x)) + 1 = 0` is
View SolutionThe number of irrational roots of the equation
` (x-1) (x-2) (3x-2) ( 3x +1) =21 ` is
View SolutionProduct of roots of the equation `x - sqrt(3 x - 6) = 2` is
View SolutionNumber of roots of the equation `2sqrt(2x+1)=2x-1` is 0 (b) 1 (c) 2 (d) 3
View SolutionProduct of roots of the equation `sqrt(13 - x^(2)) = x + 5` is
View SolutionThe number of roots of the equation `sqrt(x^2-4) -(x- 2) = sqrt(x^2 - 5x +6)` is
View SolutionThe product of the roots of the equaiton `sqrt(x^(2) - 4x + 3 ) + sqrt(x^(2) - 7x + 12) = 3 sqrt(x - 3)` is
View SolutionSuppose a and b satisfy the equations `18 a^(2) + 77 a + 2 = 0 and 2b^(2) + 77b + 18 = 0` then value of `(ab + a + 1)/( b)` is
View SolutionSuppose `alpha, beta` are roots of `x^(2)-7x+8=0,` with `alpha gt beta,` then value of `(16)/(alpha)+3 beta^(2)-19 beta` is
View SolutionIf `alpha ` is a root of `x^(4) + x^(2) - 1 = 0` , the value of `(alpha^(6) + 2 alpha^(4))^(2012)` is
View SolutionSum and product of all the roots of the equation `(x^(2)-x-1)(x^(2)-x-2)(x^(2)-x-3)...(x^(2)-x-2012)=0` is
View SolutionSuppose three distinct non-zero real numbers satisfy `a^(2) (a + k) = b^(2) (b + k) = c^(2) (c + k)` , where k is some real number, then value of `(1)/(a) +(1)/(b) +(1)/(c) ` is
View Solution
Exercise ( Level 1 (single correct answer type questions)) questions and complete solutions for chapter QUADRATIC EQUATIONS of MCGROW HILL EDUCATION MATHS (HINGLISH) of Class 12
All Exercises from MCGROW HILL PUBLICATION Class 12 MATHS QUADRATIC EQUATIONS
- Exercise ( Level 1 (single correct answer type questions))
- Exercise ( Level 2 (single correct answer type questions))
- Exercise ( Level 2 (Numerical answer type questions))
- Exercise (Concept-based single correct answer type questions)
- Questions from Previous Years. AIEEE/JEE main papers
- Questions from previous Years. B - architecture entrance examination papers
- Solved Examples (Level 1 ( Single Correct Answer Type Questions)
- Solved Examples (Level 2 (Straight Objective Type Questions))
- Solved Examples (Numerical Answer Type Questions)
- Solved Examples (Concept - based (Single Correct Answer Type Questions ))