Complete Solutions to METHEMATICS of chapter MHTCET 2011 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MHTCET 2011 |
| MHTCET PREVIOUS YEAR PAPERS | METHEMATICS |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
The multiplicative inverse of `A = [(cos theta,-sin theta),(sin theta,cos theta)]`is
View SolutionThe value of a for which system of equation , `a^3x+(a+1)^3y+(a+2)^3z=0, ax+(a+1)y+(a+2)z=0, x+y+z=0,` has a non-zero solution is:
View SolutionThe angle between a pair of tangents from a point P to the circe `x^2 + y^2+ 4 x-6y + 9 sin2 alpha + 13 cos^2 alpha =0` is `2alpha`. Find the equation of the locus of the point P.
View SolutionIf one of the lines of the pair `ax^(2)+2hxy+by^(2)=0` bisects the angle between positive direction of the axes, then a, b and h satisfy the relation.
View SolutionIf the pair of straight lines `x^2 - 2pxy - y^2 = 0` and `x^2 - 2qxy -y^2 = 0` be such that each pair bisects the angle between the other pair, then
View SolutionIf the circles `x^2+y^2+2x+2ky+6=0` and `x^2+y^2+2ky+k=0` intersect orthogonally then k equals (A) `2 or -3/2` (B) `-2 or -3/2` (C) `2 or 3/2` (D) `-2 or 3/2`
View SolutionThe equation of a circle which has a tangent `3x+4y=6` and two normals given by `(x-1)(y-2)=0` is
View SolutionThe equation of the common tangents to the circle`(x-3)^(2)+y^(2)=9` and the parabola `y^(2)=4ax` the x-axis, is
View SolutionFind the equations of normal to the parabola `y^2=4a x` at the ends of the latus rectum.
View SolutionFrom point `P(8,27)` tangents PQ and PR are drawn to the ellipse `(x^(2))/(4)+(y^(2))/(9)=1.` Then, angle subtended by QR at origin is
View SolutionIf the normal to the given hyperbola at the point `(c t , c/t)` meets the curve again at `(c t^(prime), c/t^(prime)),` then `t^3t^(prime)=1` (b) `t^3t^(prime)=-1` `tt^(prime)=1` (d) `tt^(prime)=-1`
View SolutionIf `vecu=veca-vecb,vecv=veca+vecb and |veca|=|vecb|=2,` then `|vecuxxvecv|` is equal to
View SolutionIf the vectors a, b and c are coplanar, then `|{:(a, b, c),(a*a, a*b,a*c),(b*a,b*b,b*c):}|` is equal to
View SolutionA vector v is equally inclined to the X-axis, Y-axis and Z-axis respectively the dirction cosines are
View SolutionIf a plane meets the coordinates axes at A, Band C, in such a way that the centroid of `Delta ABC` is at the point `(1,2,3)`, the equation of the plane is
View SolutionIf a line makes angles `alpha,beta,gamma` with the positive direction of coordinate axes, then write the value of `sin^2alpha+sin^2beta+sin^2gammadot`
View SolutionFind the angle between the following pair of lines: A lines with direction ratios 2,2,1 A line joning (3,1,4)to (7,2,12)
View SolutionIf from each of the three boxes containing 3 white and 1 black, 2 white and 2 black, 1 white and 3 black balls, one ball is drawn at random, then the probability that 2 white and 1 black balls will be drawn, is
View SolutionIf X follows the binomial distribution with parameters n=6 and p and 9p(X=4)=P(X=2), then p is
View SolutionIf `E_(1)` denots the envent sof coming sum 6 in throwing two dice and `E_(2)` be the event of coming 2 in any one of two, then `P(E_(2)//E_(1))` is
View SolutionLet ` f(x) = {{:({1+|sin x|}^(a//|sin x|)", " pi/6 lt x lt 0),(" b, " x = 0 ),(e^(tan 2x//tan 3x) ", "0ltx ltpi/6):}`
Determine a and b such that f(x) is continous at x = 0.
View SolutionIf `f(x)=e^(x)g(x),g(0)=2,g'(0)=1, then f'(0) ` is
View SolutionIf a, b, c and d are positive then `lim_(x to oo)(1+(1)/(a+bx))^(x+dx)` is eqqual
View SolutionLet `f(x+y)=f(x)*f(y)AAx , y in R`,suppose that `f(3)=3 and f^(prime)(0)=11` , then `f'(3)` is given by
View SolutionIf `G(x)=-sqrt(25-x^(2)),then lim_(xto1) (G(x)-G(t))/(x-1)` is
View SolutionAt the point x = 1 , then function
`f(x) = {{:(x^(3) - 1, 1lt x lt oo),(x - 1 , 1 - oolt x le 1):}` is
View SolutionIf `x^(p) y^(q) = (x + y)^((p + q)) " then " (dy)/(dx)=` ?
View SolutionIf ` x = 2 cos t - cos 2t , y = 2 sin t - sin 2t`, then the value of
` |(d^(2) y)/(dx^(2))|_(t= pi//2 ) `is
View Solution`y=logtan(x/2)+sin^(-1)(cosx)`, then `dy/dx` is
View SolutionThe minimum value of `(1-x+x^2)/(1+x+x^2)` for all real values of x is:
View SolutionIf `x+y=k` is normal to `y^2=12 x ,` then `k` is 3 (b) 9 (c) `-9` (d) `-3`
View SolutionA particle moves along a straight line according to the law `s=16-2t+3t^(3)`, where `s` metres is the distance of the particle from a fixed point at the end of `t` second. The acceleration of the particle at the end of `2s` is
View SolutionFind: `int[sqrt(cotx)+sqrt(tan x)]dx`
View Solution`int(x^(2))/((x sinx+cosx)^(2))dx` is equal to
View SolutionEvaluate `int_(0)^(pi)(x dx)/(1+cos alpha sin x)`,where `0lt alpha lt pi`.
View Solution`int_(pi//2)^(pi//2)(cosx)/(1+e^(x))dx` is equal to
View Solution`int_(0)^(pi//2)(1)/((1+tanx))dx=?`
View SolutionThe area bounded by the parabola `y^2 = x`, straight line `y = 4` and y-axis is
View SolutionFind the differential equation of all the circles which pass through the origin and whose centres lie on y-axis.
View SolutionIf m and n are order and degree of the differential equation `((d^2y)/(dx^2))^5+(4((d^2y)/(dx^2))^3)/((d^3y)/(dx^3))+(d^3y)/(dx^3)=x^2-1` (A) `m=3, n=1` (B) `m=3, n=3` (C) `m=3, n=2` (D) `m=3, n=5`
View SolutionThe integrating factor of the differential equation `(dy)/(dx)(x(log)_e x)+y=2(log)_e x` is given by
View SolutionThe differential equation whose solution is `(x-h)^2+ (y-k)^2=a^2` is (a is a constant)
View SolutionA diet of a stic person must contain atleast 4000 unit of vitamins, 50 unit of proteins and 1400 calories. Two foods A and B are available at cos of Rs. 4 and Rs. 3 per unit respectively. If one unit of A contains 200 unit of vitamis, 1 unit of protein and 40 calories, while one unit of food B contains 100 unit of vitamins, 2 unit of protein and 40 calories. Formulate the problem, so that the diet be cheapest.
View SolutionThe constraints `-x_(1)+x_(2)lt 1, -x_(1)+3x_(2)le9, x_(1), x_(2)gt, 0` difines on
View SolutionBy Simpson rule taking `n=4,` the value of the integral `int _(0)^(1)(1)/(1+x^(2))dx` is equal to
View SolutionThe propositions `(p implies~p)^^(-p implies p)` is a
View SolutionThe inverse of the proposition `(p^^-q)impliesr` is
View SolutionIn a boolean algebra B, for all x,y in `B,x*(x+y)` is equal to
View SolutionFor the circuit show below, the Boolean polynomial is
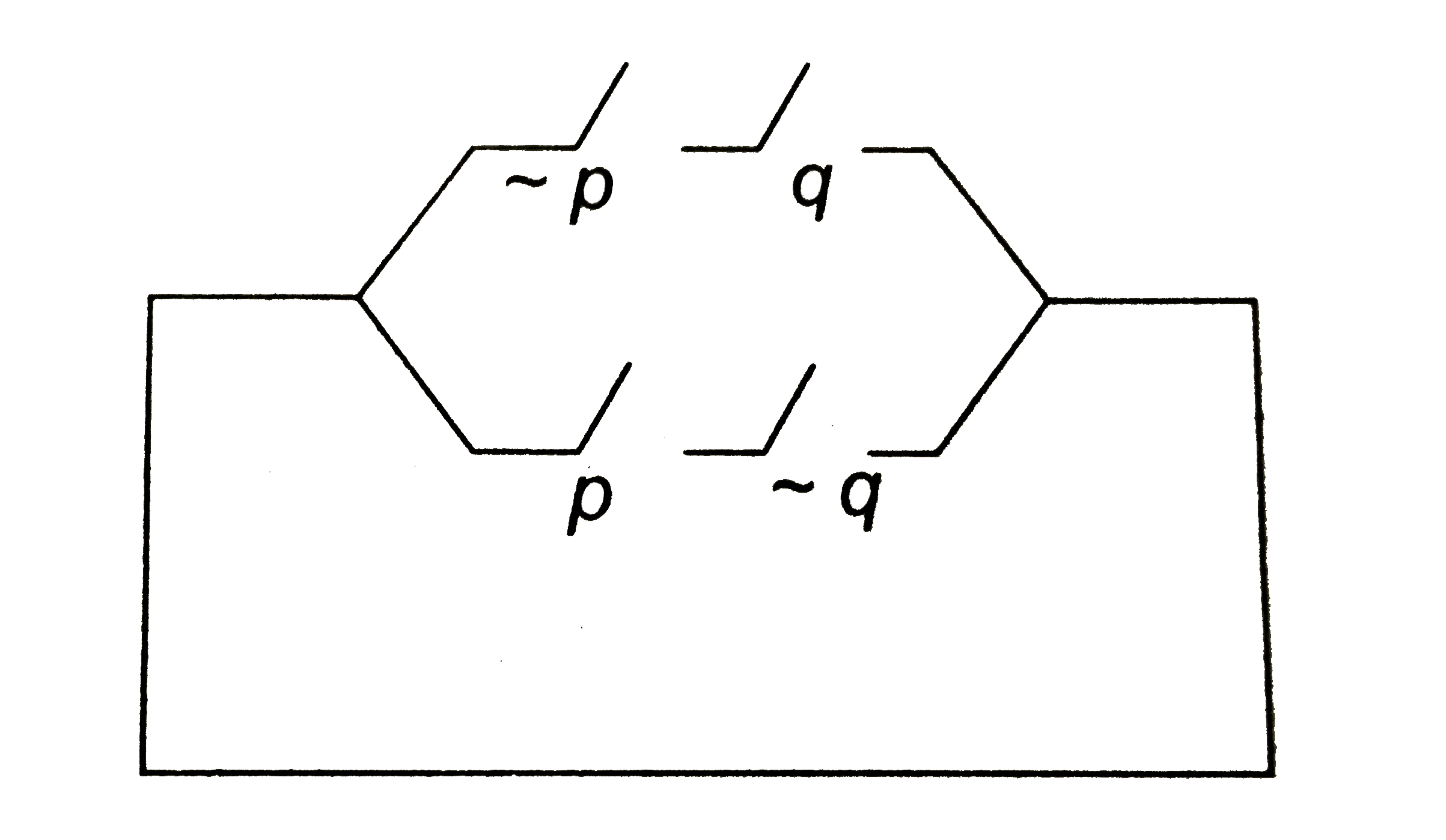
View SolutionThe value of `(1+Delta)(1-Delta)` is
View Solution
METHEMATICS questions and complete solutions for chapter MHTCET 2011 of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12