Complete Solutions to Paper - 2 (MATHEMATICS ) of chapter PRACTICE SET 16 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PRACTICE SET 16 |
| MHTCET PRACTICE PAPER | Paper - 2 (MATHEMATICS ) |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
If A = {x , y}, then the power set of A is
View SolutionIf R is a relation defined as aRb, `"iff"|a-b|gt0`, then the relation is
View SolutionThe point diametrically opposite to the point P(1, 0) on the circle `x^(2)+y^(2)+2x+4y-3=0` is
View SolutionThe centre of the circle whose radius is 5 and which touches the circle `x^(2)+y^(2)-2x-4y-20=0` at `(5,5)` is
View SolutionThe equation `y^(2)-8y-x+19=0` represents
View SolutionThe integrating factor of the differential equation `(dy)/(dx)+(y)/((1-x)sqrt(x))=1-sqrt(x)`, is
View SolutionNumber of solutions of `y=e^(x) and y=sin x` is
View SolutionThe angles A, B and C of a `Delta ABC` are in AP. If `b:c=sqrt(3):sqrt(2),` then `angle A` is equal to
View SolutionIf `sin^(-1)((3)/(x))+sin^(-1)((4)/(x))=(pi)/(2)`, then x is equal to
View SolutionThe probility that the same number appear on throwing three dice simultaneously is
View SolutionThe value of `int_(1)^(4) |x-3|dx` is equal to
View Solution`L e t` `f(x)=(1-tanx)/(4x-pi),x!=pi/4,x in [0,pi/2],` If`f(x)i s` continuous in `[0,pi/4],` then find the value of `f(pi/4)dot`
View SolutionLet the line `(x-2)/(3)=(y-1)/(-5)=(z+2)/(2)` lies in the plane `x+3y-alpha z +beta=0`. Then, `(alpha,beta)` equals
View SolutionA line line makes the same angle `theta` with each of the `x` and z-axes. If the angle `beta`, which it makes with y-axis, is such that `sin^(2)beta=3sin^(2)theta` then `cos^(2)theta` equals
View SolutionThe value of `int(x^(2)+1)/(x^(2)-1)dx` is
View SolutionIf `a=2sqrt(2),b=6,A=45^(@)`, then
View SolutionIf `y=(1+x)(1+x^2)(1+x^4)(1+x^(2n)),` then find `(dy)/(dx)a tx=0.`
View Solution`int (dx)/(sin(x-a)sin(x-b))` is
View SolutionIn `DeltaABC` `2a^2+4b^2+c^2=2ab+2ac` then numerical value of `cosB` is
View SolutionThe solution of the differential equation `(e^(-2 sqrt(x))-(y)/(sqrt(x)))(dx)/(dy)=1` is given by
View SolutionLet `f:(0,oo)to R and F(x)=int_(0)^(x) f(t)dt. " If " F(x^(2))=x^(2)(1+x)`, then f(4) equals
View Solution`lim_(nto oo)1/n+(1)/(sqrt(n^(2)+n))+(1)/(sqrt(n^(2)+2n))+...(1)/(sqrt(n^(2)+(n-1)n))` is equal to
View SolutionThe area bounded by `y = sin^(-1)x,x=(1)/(sqrt(2))` and X-axis is
View SolutionThe perpendicular distance between the line `vecr = 2hati-2hatj+3hatk+lambda(hati-hatj+4hatk)` and the plane `vecr.(hati|5hatj|hatk) = 5` is :
View SolutionIf the slope of one of the lines given by `ax^(2)+2hxy+by^(2)=0` is 5 times the other, then
View SolutionThe derivative of `f(x)=3|2+x|` at the point `x_0=-3` is
View SolutionThe curve given by `x + y = e^(xy)` has a tangent parallel to the y-axis at the point
View SolutionSwitching function of the network is
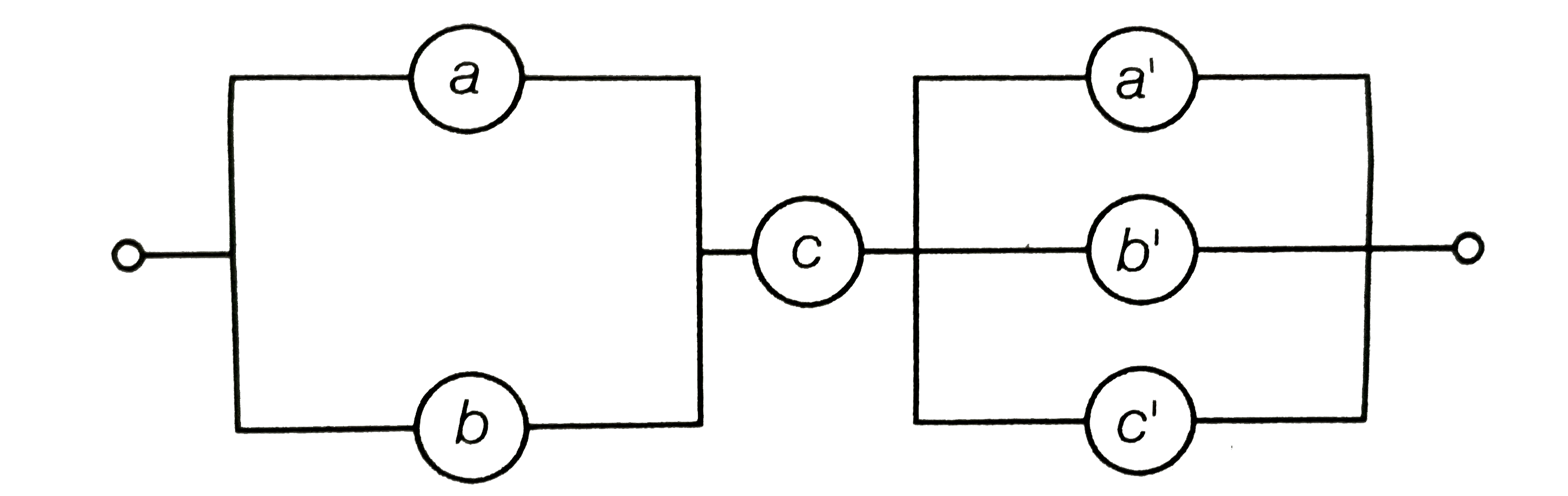
View SolutionLet p be the proposition that Mathematics is interesting and q be the proposition that Mathematics is difficult, then the symbol `p ^^ q` means
View SolutionThe equation to a pair of opposite sides of a parallelogram are `x^2-5x+6=0` and `y^2+5=0` . The equations to its diagonals are `x+4y=13 ,y=4x-7` (b) `4x+y=13 ,4y=x-7` `4x+y=13 ,y=4x-7` (d) `y-4x=13 ,y+4x-7`
View SolutionIn the adjoining circuit, the output s is
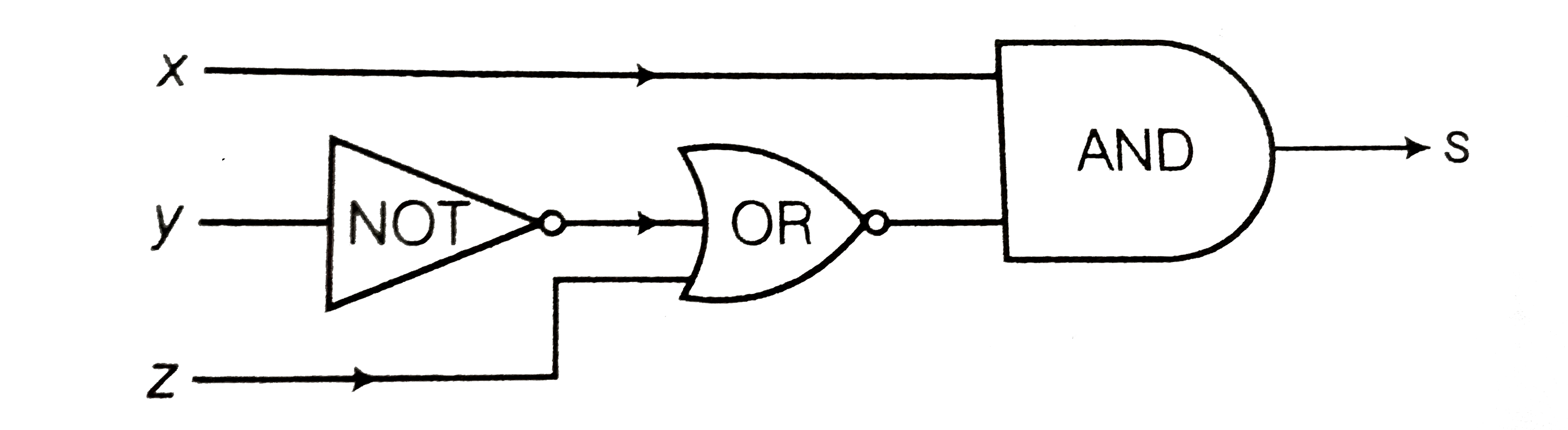
View SolutionThe slope of tangent at (x,y) to a curve passing through (2, 1) is `(x^(2)+y^(2))/(2xy)`, then the equation of the curve is
View SolutionThe value of the integral `int_3^6 sqrtx/(sqrt(9-x)+sqrtx)dx` is
View SolutionFind the probability that a leap year will have 53 Friday or 53 Saturdays.
View SolutionThe function `f(x)=x/2+2/x` has a local minimum at `x=2` (b) `x=-2` `x=0` (d) `x=1`
View SolutionTwo person `A and B` take turns in throwing a pair of dice. The first person to through 9 from both dice will win the game. If A throwns fisrt then the probability that B wins the game is.
View SolutionThe dr. of normal to the plane through `(1,0,0), (0,1,0)` which makes an angle `pi/4` with plane , `x+y=3` are
View SolutionIf twice the 11th term of an AP is equal to 7 times its 21st term, then its 25th term is equal to
View Solutionif a G.P (p+q)th term = m and (p-q) th term = n , then find its p th term
View SolutionIf `x=2+a+a^2+oo,w h e r e|a|<1a n dy=1+b+b^2+oo,w h e r e|b|<1.` prove that: `1+a b+a^2b^2+oo=(x y)/(x+y-1)`
View Solution26, The distance between the lines 3x + 4y = 9 and 6x + 8y + 15-0 is 3 10 10 (d) none of these
View SolutionThe image of the origin with reference to the line 4x+3y -25=0 is
View SolutionIf `g(x)="min"(x,x^(2))`, where x is a real number, then
View SolutionIf `sin3theta = sintheta`, how many solutions exist such that `-2piltthetalt2pi`
View SolutionIf the mean and variance of a random variable X having a binomial distribution of 8 terms, are 4 and 2, respectively. Then `P(X gt 6)` is equal to
View SolutionIf the area bounded by the curve `y= sin ax, y = 0, x=pi//a and x=pi //3a( a gt 0)`, is 3 then a is equal to
View SolutionThe shortest distance between the lines `(x-2)/(3)=(y+3)/(4)=(z-1)/(5) and (x-5)/(1)=(y-1)/(2)=(z-6)/(3)`, is
View Solution`int e^(x log a) e^(x) dx ` is equal to
View SolutionFind the intervals in which `f(x)=x^3-6x^2-36 x+2` is increasing or decreasing.
View SolutionA line with positive diection cosines passes through the ont `P(2,-1,2) and ` makes equal angles with the coordinate axes. The line meets the plane `2x=y+z=0 ` at Q. The length of the line segment PQ equals (A) `1` (B) `sqrt(2)` (C) `sqrt(3)` (D) 2
View Solution
Paper - 2 (MATHEMATICS ) questions and complete solutions for chapter PRACTICE SET 16 of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12