Complete Solutions to MATHMATICS of chapter MHTCET 2017 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MHTCET 2017 |
| MHTCET PREVIOUS YEAR PAPERS | MATHMATICS |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
The numbr of principal solution of ` tan 2 theta =1` is
View SolutionThe objective function, `z=4x_(1)+5x_(2),` subject to `2x_(1)+x_(2)ge7,2x_(1)+3x_(2)le15,x_(2)le3,x_(1),x_(2)ge0` has minimum value at the point
View SolutionIf `z_(1) and z_(2)` are z-coordinates of the points of trisection of the segment joining the points A(2,1,4), B(-1,3,6_, then `z_(1)+z_(2)+`
View SolutionThe maximum value of `f(x)=(logx)/(x)(x ne 0, x ne1)` is
View Solution`int_0^1xtan^(- 1) x dx=`
View SolutionThe statement pattern `(~p ^^ q)` is logically equivalent to
View SolutionIf g(x) is the inverse function of f(x) and `f'(x)=(1)/(1+x^(4))`, then `g'(x)` is
View SolutionThe inverse of the matrix `[(1,0,0),(3,3,0),(5,2,-1)]` is
View SolutionIf `int(1)/(sqrt(9-16x^(2)))dx=alphasin^(-1)(betax)+c`, then `alpha+(1)/(beta)=`
View SolutionO(0,0), A(1,2), B(3,4) are the vertices of `DeltaOAB`. The joint equation of the altitude and median drawn from O is
View SolutionIf the function `f(x) = [tan(pi/4 + x)]^(1/x)` for `x ne 0` is `= K` for x = 0
View SolutionFor a invertible matrix A if `A(adjA)=[(10,0),(0,10)]`, then |A|=
View SolutionThe solution of the differential equation `(dy)/(dx)="tan"((y)/(x))+(y)/(x)` is
View SolutionIn `DeltaABC`, if `sin^(2)A+sin^(2)B=sin^(2)C and l(AB)=10,` then the maximum value of the area of `DeltaABC` is
View SolutionIf `x=f(t)` and `y=g(t)` , then write the value of `(d^2y)/(dx^2)` .
View SolutionThe equation of line equally inclined to coordinate axes and passing through (-3,2,-5) is
View Solution`int_0 ^ (pi/2) log(cosx) dx=`
View SolutionA boy tosses faiir coin 3 times. If he gets Rs 2X for X heads, then his expected gain equals to Rs…..
View SolutionWhich of the following statement pattern is a tautology?
View SolutionIf the angle between the planes `r.(mhati-hatj+2hatk)+3=0 and r*(2hati-mhatj-hatk)-5=0` is `(pi)/(3)`, then m=
View SolutionIf the origin and the points P(2,3,4), Q(1,2,3) and R(x,y,z) are coplanar, then
View Solutionif lines represented by equation `px^(2)-qy^(2)=0` are distinct, then
View SolutionLet `square PQRS` be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
View SolutionIf slopes of lines represented by `kx^(2)+5xy+y^(2)=0` differ by 1, then k=
View SolutionIf vector r wiith dc's l,m,n is equally inclined to the coordinate axes, then the total number of such vectors is
View SolutionIf `int(1)/((x^(2)+4)(x^(2)+9))dx=A" tan"^(-1)(x)/(2)+Btan^(-1)((x)/(3))+C`, then A-B=
View SolutionIf `alpha and beta` are roots of the equation `x^(2)+5|x|-6=0,` then the value of `|tan^(-1)alpha-tan^(-1)beta|` is
View SolutionIf `x=a(t-(1)/(t)),y=a(t+(1)/(t))`, where t be the parameter, then `(dy)/(dx)=?`
View SolutionThe point on the curve `y=sqrt(x-1)`, where the tangent is perpendicular to the line 2x+y-5=0 is
View SolutionIf `intsqrt((x-5)/(x-7))dx = A sqrt(x^(2) - 12 x + 35) + log|x-6 +sqrt(x^(2)-12x+35)| + C`, then
View SolutionAt random variable `X~B(n,p)` if values of mean and variance of X are 18 and 12 respectively, then total number of possible values of X are
View SolutionThe area of the region bounded by the lines y=2x+1y=3x+1 and x=4 is
View SolutionA box contains 6 pens, 2 of which are defective. Two pens are taken randomly from the box. If `r.v.X`, number of defective pens obtained , then standard deviation
View SolutionIf the volume of spherical ball is increasing at the rate of `4pi" cc/s"`, then the rate of change of its surface area when the volume is 288 `pi` cc is
View SolutionIf `f(x)=log(sec^(2)x)^(cot2)` for `xne0` for x=0 is continuous at x=0, then K is
View SolutionIf c denotes the contradication, then dual of the compound statement `~p ^^ (q vv c)` is
View SolutionThe differential equation of all parabolas whose axis are parallel to the y-axis is (a) `( b ) (c) (d)(( e ) (f) d^(( g )3( h ))( i ) y)/( j )(( k ) d (l) x^(( m )3( n ))( o ))( p ) (q)=0( r )` (s) (b) `( t ) (u) (v)(( w ) (x) d^(( y )2( z ))( a a ) x)/( b b )(( c c ) d (dd) y^(( e e )2( f f ))( g g ))( h h ) (ii)=C (jj)` (kk) (c) `( d ) (e) (f)(( g ) (h) d^(( i )3( j ))( k ) y)/( l )(( m ) d (n) x^(( o )3( p ))( q ))( r ) (s)+( t )(( u ) (v) d^(( w )2( x ))( y ) x)/( z )(( a a ) d (bb) y^(( c c )2( d d ))( e e ))( f f ) (gg)=0( h h )` (ii) (d) `( j j ) (kk) (ll)(( m m ) (nn) d^(( o o )2( p p ))( q q ) y)/( r r )(( s s ) d (tt) x^(( u u )2( v v ))( w w ))( x x ) (yy)+2( z z )(( a a a ) dy)/( b b b )(( c c c ) dx)( d d d ) (eee)=C (fff)` (ggg)
View Solution`int_(0)^(x) dx = "……."`, where [x] is greatest integer function.
View SolutionObjective function of an LPP is
View SolutionIf the inverse of the matriix `[(alpha,14,-1),(2,3,1),(6,2,3)]` does not exist, then the vlaue of `alpha` is
View SolutionIf `f(x) = x` for `x le 0 = 0 ` for `x gt 0`, then `f(x)` at `x = 0` is
View SolutionThe equation of the plane through (-1,1,2), whose normal makes equal acute angles with coordinate axes is
View SolutionProbability that a person will develop immunity after vaccinations is 0.8. if 8 people are givenn the vaccine, then probability that all develop immunity is=
View SolutionIf the distance of points `2hati+3hattj+lamdahatk` from the plane `r*(3hati+2hatj+6hatk)=13` is 5 units, then `lamda=`
View SolutionThe value of `cos^(-1)(cot((pi)/(2)))+cos^(-1)(sin((2pi)/(3)))` is
View SolutionThe particular solution of the differential equation xdy + 2 y dx = 0, when x = 2,
View Solution`A B C` is a triangle and `A=(235)dotB=(-1,3,2)a n dC=(lambda,5,mu)dot` If the median through `A` is equally inclined to the axes, then find the value of `lambdaa n dmudot`
View SolutionFor the following distribution function `F(x)` of a rv.X.
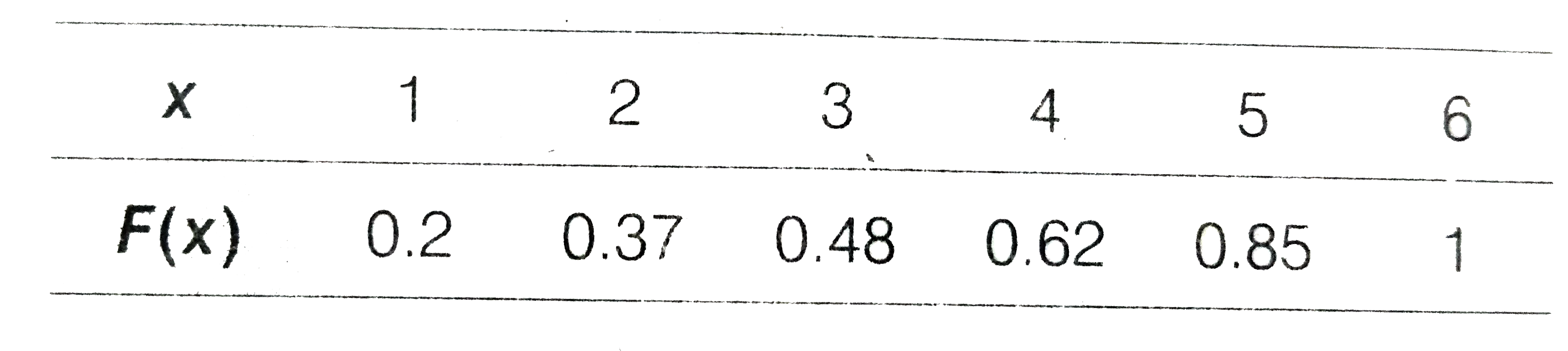
`P (3 lt x le 5) = `
View SolutionThe lines `(x-1)/(2)=(y+1)/(2)=(z-1)/(4) and (x-3)/(1)=(y-k)/(2)=(z)/(1)` intersect each other at point
View Solution`int(sec^(8)x)/(cosecx) dx =`
View Solution
MATHMATICS questions and complete solutions for chapter MHTCET 2017 of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12