Complete Solutions to Paper 2 (Mathmatics) of chapter PRACTICE SET 24 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PRACTICE SET 24 |
| MHTCET PRACTICE PAPER | Paper 2 (Mathmatics) |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
The switching function for the following network is
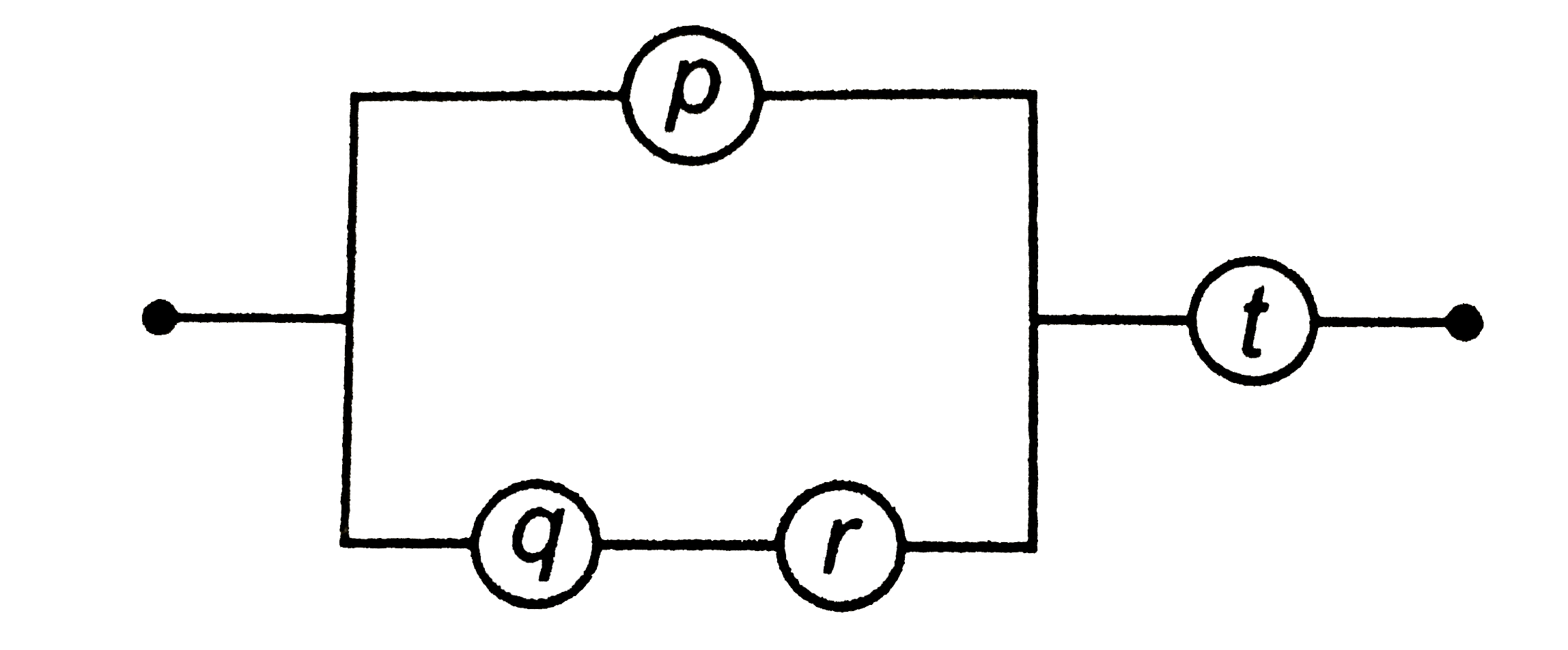
View SolutionFind the incentre of the triangle with vertices `(1, sqrt3), (0, 0)` and `(2, 0)`
View SolutionFind the length of the latus rectum of the parabola `169{(x-1)^2+ (y -3)^2} =(5x-12y + 17)^2`.
View SolutionThe solution set of the inequation `2x+y gt 5` is
View SolutionLet A and B be two events such that `P(A)=0.3` and `P(AuuB)= 0.8`. If A and B are independent events, then `P(B)=`
View SolutionIf `sin^(-1)x+sin^(-1)y=pi/2`, then `dy/dx` is equal to
View Solution`int((tan^(-1)x)^(3))/(1+x^(2))dx` is equal to
View SolutionThe solution of `(dy)/(dx) = 2^(y-x)` is
View SolutionIf the line y = 7x - 25 meets the circle `x^(2) + y^(2) = 25` in the points A,B then the distance between A and B is
View SolutionDual of `x*(y+x) = x` is
View SolutionThe angle between the tangents drawn at the points `(5,12)` and `(12,-5)` to the circle `x^2+y^2=169` is:
View SolutionEquation of radical axis of the circles `x^(2) + y^(2) - 3x - 4y + 5 = 0` and `2x^(2) + 2y^(2) - 10x - 12y + 12 = 0` is
View SolutionGiven two vectors are `hati-hatj and hati+2hatj`. The unit vector coplanar with the two vectors nad perpendicular to first is (A) `1/sqrt(2)(hati+hatj)` (B) `1/sqrt(5)(2hati+hatj)` (C) `+-1/sqrt(2)(hati+hatj)` (D) none of these
View SolutionThe value of `lim_(x to 7) ((2 - sqrt(x - 3))/(x^(2) - 49))` is
View SolutionIf `4x^(2)+ py^(2) =45` and `x^(2)-4y^(2) =5` cut orthogonally, then the value of p is
View Solution`int_0^(pi)e^(sin^2x)cos^3xdx`
View SolutionIf the sum of 12th and 22nd terms of an AP is 100 then the sum of the first 33 terms of an AP is
View SolutionThe negation of the statement `''2 + 3 = 5 and 8 lt 10` is-
View SolutionIf `[{:( 2 + x , 3 , 4 ) , (1 , -1 , 2 ) , (x , 1 , -5):}]` is a singular matrix then x is
View SolutionA straight line through `P(1,2)` is such that its intercept between the axes is bisected at `P` its equation :
View SolutionThe eccentricity of an ellipse with its centre at the origin is `(1)/(2) ` . If one of the directrices is x = 4 , then the equation of ellipse is
View SolutionThe diection cosines of two lines are proportional to `(2,3,-6) and (3,-4,5),` then the acute angle between them is (A) `cos^-1{49/36}` (B) `cos^-1 {(18sqrt(2))/35}` (C) `96^0` (D) `cos^-1(18/35)`
View SolutionFind the probability that a leap year will have 53 Friday or 53 Saturdays.
View SolutionIf `f(x)=sqrt(1+cos^2(x^2)),t h e nf^(prime)((sqrt(pi))/2)` is `(sqrt(pi))/6` (b) `-sqrt(pi//6)` `1//sqrt(6)` (d) `pi//sqrt(6)`
View SolutionThe sum of the series `1^(3) + 2 ^(3) + 3^(3) + ...+15^(3)` is
View SolutionDegree of the differential equation `e^(dy/dx)` = x is
View SolutionIn a Boolean Algebra B, for all x in B. 1' is equal to
View SolutionA survey shows that 63% of the Americans like cheese 4 whereas 76% like apples. If x% of the Americans likes both cheese and apples, find the value of x.`(39<=x<=63)`
View SolutionCircle `x^2 + y^2 - 2x - lambdax - 1 = 0` passes through to fixed points, coordinates of the points are
View SolutionIf `|a| = 3 , |b| = 4 ` , then a value of `lamda` for which `a + lamda b ` is perpendicular to `a - lamda b` is
View SolutionThe minimum value of P = 6x + 16y subject to constraints `x le 40 , y le 20 ` and `x , y ge 0` is
View SolutionIf a dice is thrown twice, the probability of occurrence of 4 atleast once is
View SolutionIf ` y = tan^(-1) (sec x - tan x ) , "then" (dy)/(dx)` is equal to
View Solution`int_(0)^(8)|x-5|dx=17`
View SolutionLet A = {1, 2, 3, 4) and R be the relation on A defined by {(a, b) : a, be A, a × b is an even number}, then the range of R is
View SolutionWhich of the following is not a statement ?
View SolutionThe number of point at which the function `f(x)=|x-1|+[x-2]+cosx,` where `x in [0,4]` is not continuous, is `([.]` denotes greatest intergest function}
View SolutionThe radius of a cylinder is increasing at the rate of `3ms^(-1)` and its altitude is decreasing at the rate of `4ms^(-1)`. The rate of change of volume when radius is `4m` and altitude is 6m is
View SolutionIntegrating factor of differential equation `cosx(dy)/(dx)+ysinx=1` is (a) `( b ) (c)cosx (d)` (e) (b) `( f ) (g)tanx (h)` (i) (c) `( d ) (e)secx (f)` (g) (d) `( h ) (i)sinx (j)` (k)
View SolutionFind the output for the given input for the given circuit
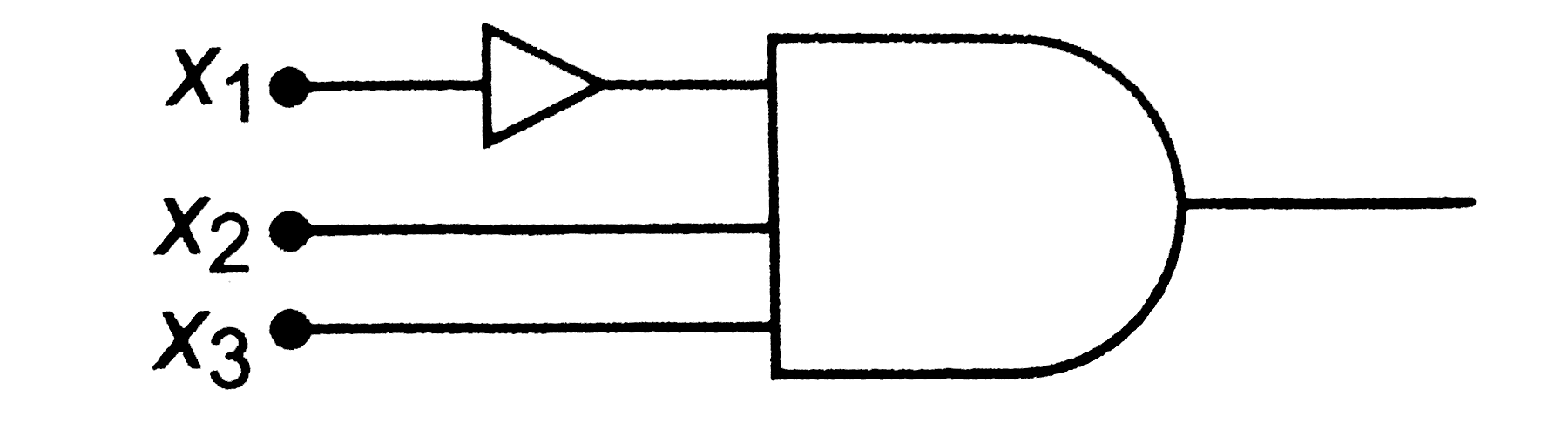
View SolutionLet S be set of all real numbers and let R be relation on s , defined by `a R b hArr |a-b|le 1.` then R is
View SolutionIf e and e' are the eccentricities of the ellipse `5x^(2) + 9 y^(2) = 45 ` and the hyperbola `5x^(2) - 4y^(2) = 45` respectively , then `ee'` is equal to
View SolutionIf O is origin and C is the mid - point of A (2, -1) and B ( -4, 3) . Then value of OC is
View SolutionA letter is taken out at random from 'ASSISTANT and another is taken out from 'STATISTICS. The probability that they are the same letters, is
View SolutionIF t is a parameter, then `x = a(t + (1)/(t))` and `y = b(t - (1)/(t))` represents
View Solution`int(x^(2) - 1)/(x^(4) + x^(2) + 1) dx` is equal to
View Solution`int_(-1)^(0) (dx)/(x^(2) + 2x + 2 )` is equal to
View SolutionThe number of normals drawn to the parabola `y^2 =4x` from the point `(1,0)` is
View SolutionIf `A, B, C` are the vertices of a triangle whose position vectros are `vec a,vec b, vec c and G` is the centroid of the `DeltaABC,` then `overline(GA)+overline(GB)+overline(GC) =`
View SolutionIf `y="sec"(tan^(-1)x),` then `(dy)/(dx)` at `x=1` is equal to: `1/(sqrt(2))` (b) `1/2` (c) 1 (d) `sqrt(2)`
View Solution
Paper 2 (Mathmatics) questions and complete solutions for chapter PRACTICE SET 24 of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12