Complete Solutions to PRACTICE EXERCISE (Exercies 1 (TOPICAL PROBLEMS)) of chapter MATHEMATICAL LOGIC of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MATHEMATICAL LOGIC |
| MHTCET PREP GUIDE | PRACTICE EXERCISE (Exercies 1 (TOPICAL PROBLEMS)) |
| Number Of Questions | 52 |
| Academic Year | 2023-24 |
The conditional statement of "You will get a sweet dish after the dinner" is
View SolutionWhich of the following is not a proposition ?
View SolutionIf p,q and r are simple propositions with truth values T,F and T , respectively, then the truth value of `(~pvvq) ^^~r to p` is
View SolutionIn the truth table for the statement `(~ p rArr ~ q) ^^ (~ q rArr ~p)`, the last column has the truth value in the following order
View SolutionThe false statement among the following is
View SolutionFor the following three statements
p : 2 is an even number
q : 2 is a prime number
r : Sum of two prime numbers is always even.
Then, the symbolic statement `(p ^^ q) rArr ~ r` means
View SolutionLet p be the proposition that Mathematics is interesting and q be the proposition that Mathematics is difficult, then the symbol `p ^^ q` means
View SolutionFor two statement p and q
p : A quadrilateral is a parallelogram
q : The opposite sides are parallel
Then, the compound proposition, ''A quadrillateral is a parallelogram if and only if the opposite sides are parallel'' is represented by
View SolutionConsider the following statements :
p: He is intelligent
q: He is strong
Then symbolic form of statements 'it is wrong that he is intelligent or strong's
View SolutionThe converse of the contrapositive of the conditional `p to ~ q` is
View SolutionIf p,q and r simple propositions with truth values T, F, T, then the truth value of `(~p vv q) ^^ ~ q to p` is
View SolutionThe contrapositive of `(p vv q)to r` is
View SolutionIf `(p^^~r) to (~p vvq)` is false, then truth values of p,q and r are respectively.
View SolutionThe contrapositive of ''If two triangles are identical, then these are similar'' is
View SolutionWhich of the following is the proposition ?
''If a number is a prime, then it is odd''.
View SolutionThe statement `(~p ^^ q) vv ~ q` is equivalent
View Solution`(~(~p))^^q` is equal to
View SolutionThe statement `p to(q to p)` is equivalent to
View Solution`~(p vv q)vv (~p ^^ q)` is logically equivalent to
View SolutionWhich of the following is True?
View SolutionThe logically equivalent proposition of `p iff q` is
View Solutionlogically equivalent to `~(~p=>q)` is
View SolutionLet p and q be two statements, then `(p vv q)vv ~p` is
View SolutionThe statement `(p rArr q) iff (~p ^^ q)` is a
View SolutionLet p and q be two statements. Then, `(~p vv q) ^^ (~p ^^ ~q)` is a
View SolutionIf p and q are two statements, then `(p rArr q) iff (~q rArr ~ p)` is
View SolutionIf p and q are two stastements, then stastement `p rArr p ^^ ~ q` is a
View SolutionThe statement `~(p->q) <- > (~p vv ~q)` is-:
View SolutionThe proposition `S : (p rArr q) iff (~p vv q)` is a
View Solution`~(pvvq)vv(~p^^q)` is equivalent to
View SolutionLet p and q be two statements, then `(p vv q)vv ~p` is
View SolutionThe statement `p to(q to p)` is equivalent to
View SolutionWhich of the following statements is a tautology ?
View SolutionWhich of the following is an example of quantifiers ?
View SolutionThe dual of the statement `(p vv q) ^^ ~(r vv s)` is
View SolutionThe dual of the statement `((p^^ q) ^^ ~q)vv (~q)` is
View SolutionWrite the negation of the following statement: `r :` There exists a number `x` such that `0
View SolutionThe negation of the statement
p : ''For every positive real number x, the number x - 1 is also positive'' is
View SolutionGiven, 'Sachin score runs but India does not win the match is statement.
Statement I The symbolic form is `p ^^ ~ q`.
Statement II Negation is 'Sachin not score runs or India win the match.
Where P : Sachin score runs
q : India win the match.
View SolutionLet S be a non-empty subset of R. Consider the statement P : There is a rational number `x in S` such that `x gt 0`.
Which of the following statements is the negation of the statement P ?
View SolutionLet p : 7 is not greater than 4 and q : Paris is in France be two statements. Then, `~(p vv q)` is the statement
View SolutionThe negation of the proposition ''If 2 prime, then 3 is odd'' is
View Solution`(~(~p))^^q` is equal to
View SolutionThe negation of the compound proposition is `p vv (~ p vv q)`
View SolutionThe negation of `p ^^ (q to ~ r)` is
View SolutionNegation of ''London is in England and Berut is in Lebnan'' is
View SolutionThe simplified circuit for the following circuit is
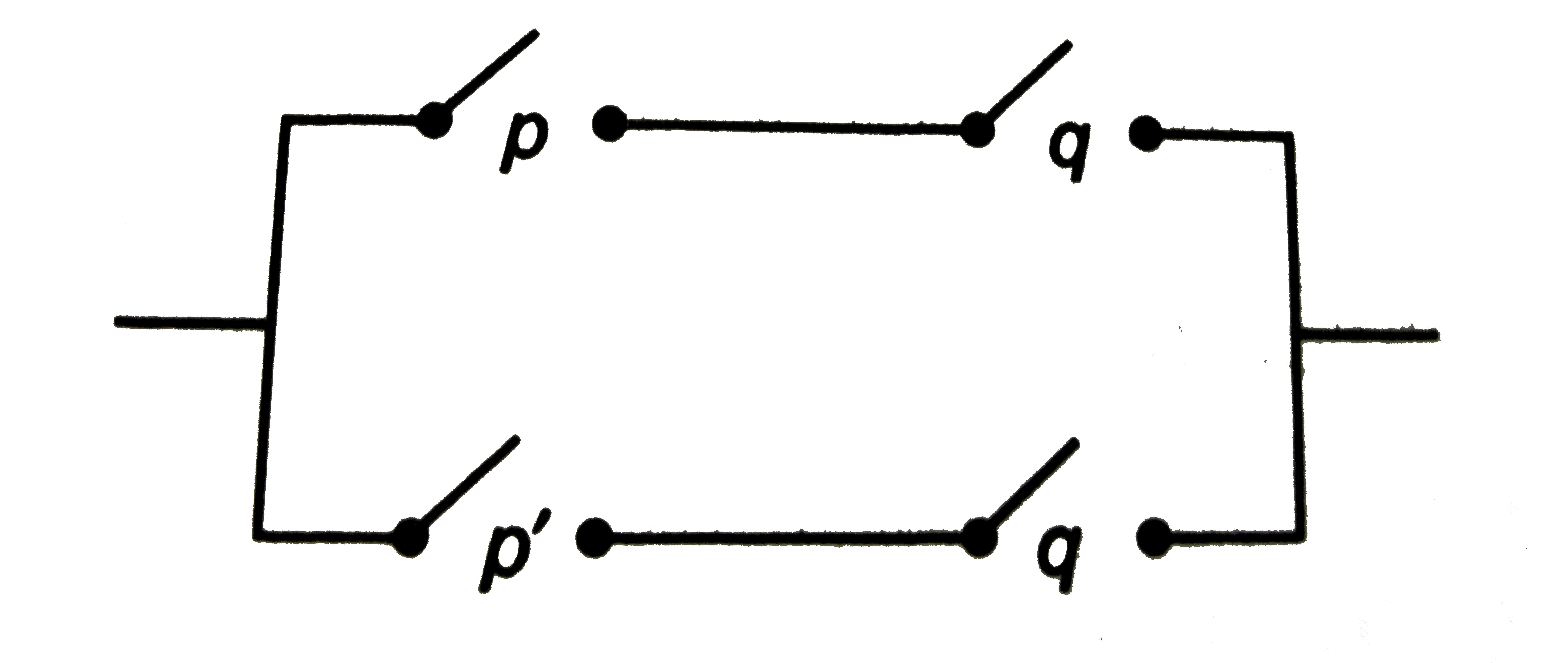
View SolutionConsider the circuit
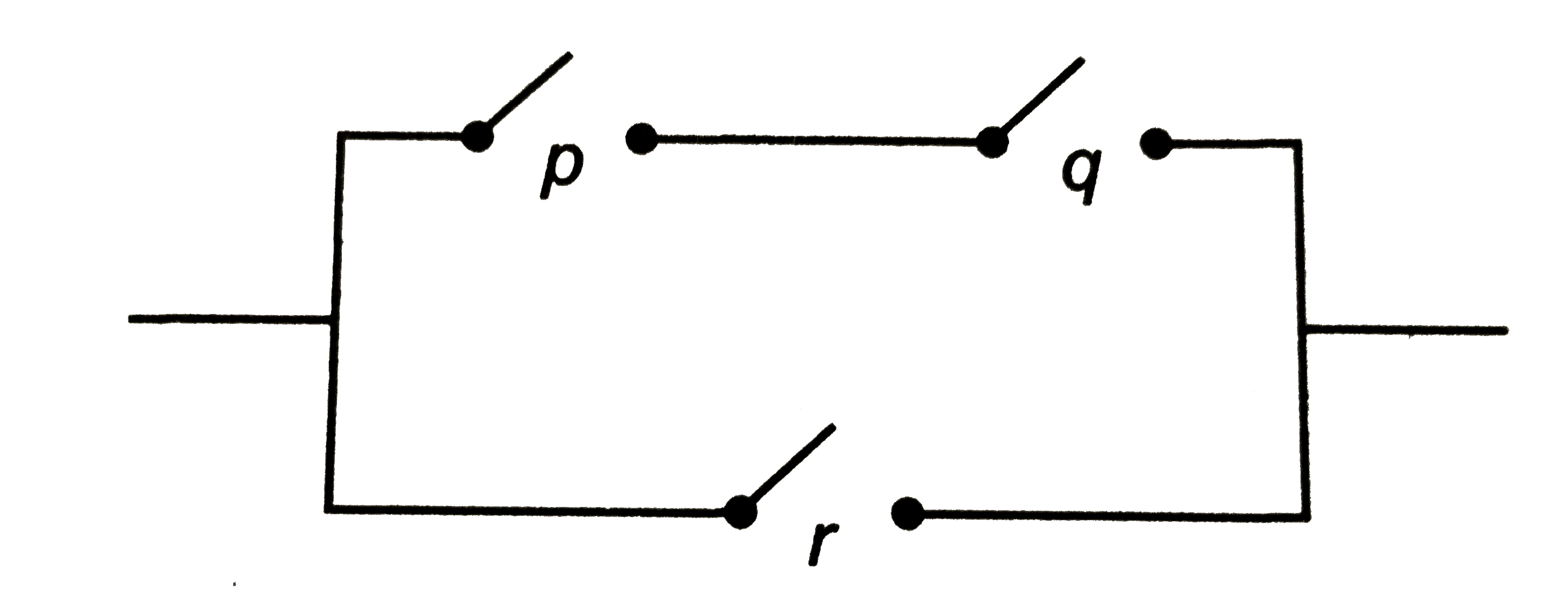
Then, the current flow in the circuit is
View SolutionThe simplified circuit for the following circuit is
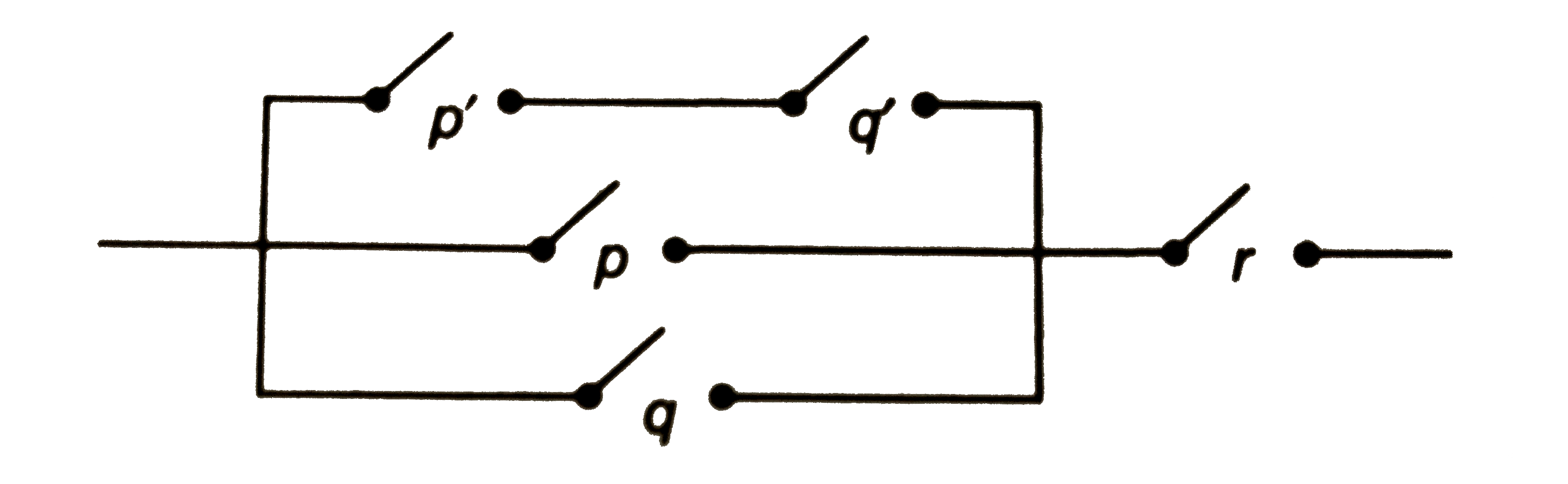
View SolutionConsider the switching circuit given below :
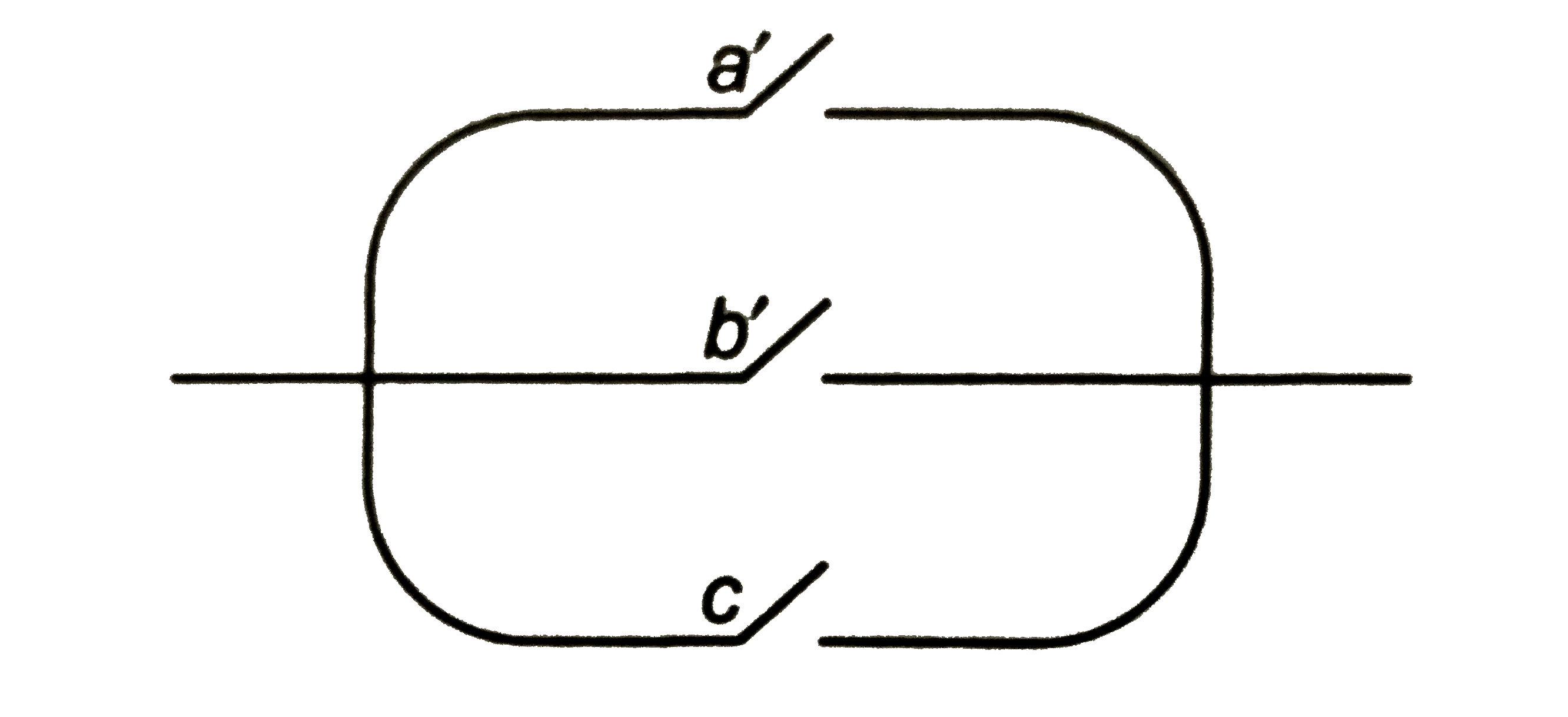
Then, the current flow in the circuit is
View SolutionQuivalent circuit for the logical expression `(~p ^^ q) vv (~p ^^ ~q) vv (p ^^ ~q)` is
View SolutionConsider the switching circuit given below
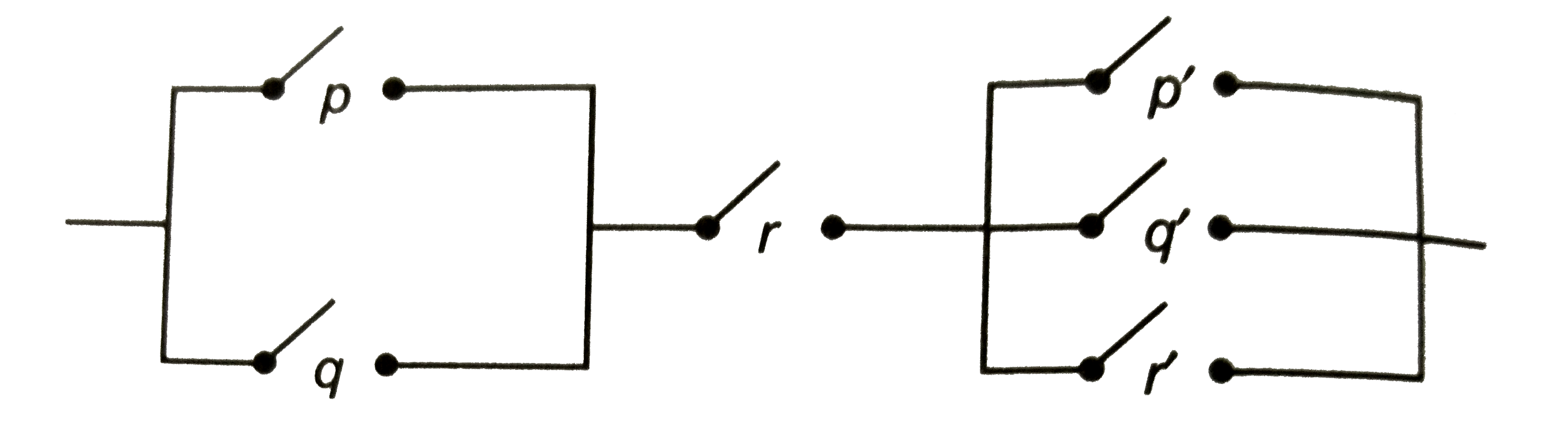
Then, the current flow in the circuit is
View Solution
PRACTICE EXERCISE (Exercies 1 (TOPICAL PROBLEMS)) questions and complete solutions for chapter MATHEMATICAL LOGIC of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12