Complete Solutions to EXERCISE 1 of chapter ELASTICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELASTICITY |
| MHTCET PREP GUIDE | EXERCISE 1 |
| Number Of Questions | 66 |
| Academic Year | 2023-24 |
The following four wires of length L and radius r are made of the same material. Which of these will have the largest extension, when the same tension is applied?
View SolutionA sphere or radius 3 cm is subjected to a pressure of 100 atm. Its volume decreases by 0.3 cc. What will be its bulk modulus?
View SolutionTo break a wire of 1 m length, minimum 40 kg weight is required. Then, the wire of the same material of double radius and 6 m length will require breaking weight.
View Solutionwhen a weight of 10 kg is suspended from a copper wire of length 3m and diameter 0.4 mm. Its length increases by 2.4 cm. If the diameter of the wire is doubled then the extension in its length will be
View SolutionA force of `6 xx 10^(6) Nm^(-2)` required for breaking a material. The denisty `rho` of the material is `3 xx 10^(3) kg m^(-3)`. If the wire is to break under its own weight, then the length of the wire made of that material should be (Given, g = 10 `ms^(-2)`)
View SolutionThe length of the wire is increased by 2% by applying a load of 2.5 kg-wt. what is the linear strain produced in the wire?
View SolutionThe breaking force for a wire of diameter D of a material is F. The breaking force for a wire of the same material of radius D is
View SolutionA copper wire and a steel wire of the same diameter and length are joined end and a force is applied which stretches their combined length by 1 cm. Then, the two wires will have
View SolutionA substance breaks down by a stress of `10^(6) Nm^(-2)`. If the density of the material of the wire is `3 xx 10^(3) kgm^(-3)`. Then the length of the wire of the substance which will break under its own weight when suspended vertically is
View SolutionThe breaking stress of a wire depends on
View SolutionTwo wires of equal cross-section but one made of steel and the other of copper are joined end to end. When the cobination is kept under tension, the elongations in the two wires are found to be equal elongations in the two wire are found to be equal. What is the ratio of the lengths of the two wires?
(Given, Young's modulus of steel `= 2 xx 10^(11) Nm^(-2)` and young's modulus of copper `= 1.1 xx 10^(11) Nm^(-2)`)
View SolutionThe Young's modulus of brass and steel are respectively `1.0 xx 10^(11) Nm^(-2)` and `2.0 xx 10^(11) Nm^(-2)`. A brass wire and a steel wire of the same length are extended by 1 mm each under the same force. If radii of brass and steel wires are `R_(B)` and `R_(s)` respectively, then
View SolutionA tangential force of 0.25 N is applied to a 5 cm cube to displace its upper surface with respect to the bottom surface. The shearing stress is
View SolutionThe adjacent graph shows the extension `(Delta I)` of a wire of lenth 1 m suspended from the top of a root at one end with a load w connected to the other end. It the cross-sectional area of the wire is `10^(-6) m^(2)`, then calculate the Young's modulus of material of the wire
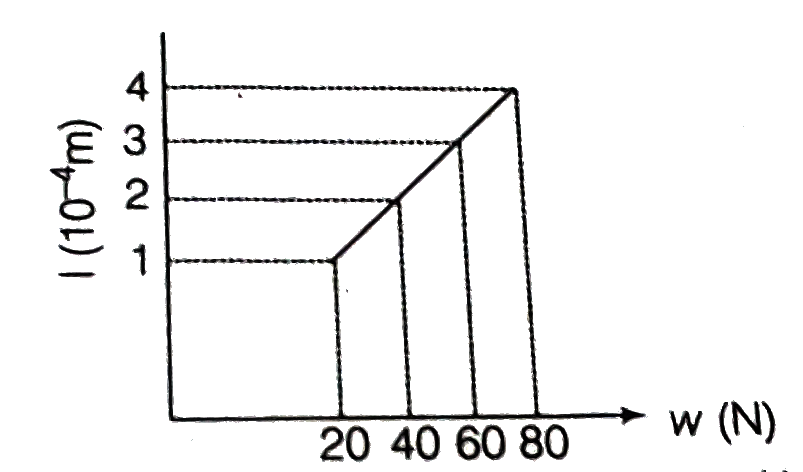
View SolutionA body subjected to strain a number of times does not obey Hook's law due to
View SolutionWhich of the following statements is wrong?
View SolutionA stress of `3.18 xx 10^(8) Nm^(-2)` is applied to a steel rod of length 1m along its length, its Young's modulus is `2 xx 10^(11) Nm^(-2)`. Then the elongation produced in the rod (in mm) is
View SolutionThe young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced to` L/2` and radius `r/2` , then its young's modulus will be
View SolutionAn iron rod of length 2 m and cross-sectional area of `50 mm^(2)` is stretched by 0.5 mm, when a mass of 250 Kg is hung from its lower end. Young's modulus of iron rod is
View SolutionA particular force (F) applied on a wire increases its length by `2 xx 10^(-3)` m. To increases the wire's length by `4 xx 10^(-3)` m, the applied force will be
View SolutionWhen a sphere is taken to bottom of sea 1 km deep, it contracts by 0.01%. The bulk modulus of elasticity of the material of sphere is
(Given density of water = 1 g `cm^(-3)`)
View SolutionA copper bar of length L and area of cross-section A is placed in a chamber at atmospheric pressure. If the chamber is evacuated, then the percentage change in its volume will be (Given, compressibility of copper is `8 xx 10^(12) m^(2) N^(-1)` and 1 atm `= 10^(5) Nm^(-2)`)
View SolutionA ball falling in a lake of depth `200 m` shows a decrease of `0.1% ` in its volume at the bottom. The bulk modulus of elasticity of the material of the ball is (take `g = 10 ms^(-2)`)
View SolutionWhen a rubber cord is stretched, the change in volume with respect to change in its linear dimensions is negligible. The Poisson's ratio for rubber is
View SolutionA uniform cube is subjected to volume compression. If each side is decreased by 1 % then bulk strain is
View SolutionFor most materials the Youngs modulus is n times the modulus of rigidity, where n is
View SolutionIn the three states of matter, the elastic coefficient can be
View SolutionFor a wire of length L, maximum change in length under stress condition is 2 mm. What is the change in length under same conditions when length of wire is halved?
View SolutionTo what depth below the surface of sea should a rubber ball be taken as to decreases its volume by 0.1% (Given denisty of sea water = 1000 kg `m^(-3)`, Bulk modulus of rubber `= 9 xx 10^(8) Nm^(-2)`, acceleration due to gravity `= 10 ms^(-2)`)
View SolutionOne end of a unifrom wire of length L and weigth W is attached rigidly to a point in the roof and a weight `W_(1)` is suspended from its lower end. If S is the area of cross-section of the wire then the stress in the wire at a height `(3L)/(4)` from its lower end is
View SolutionA 5 aluminium wire `(Y = 7 xx 10^(10) Nm^(-2)`) of diameter 3 mm supports a 40 kg mass. In order to have the same elongation in a copper wire `(Y = 12 xx 10^(10) Nm^(-2)`) of the same length under the same weight, the diameter (in mm) should be
View SolutionFour identical rods are stretched by same force. Maximum extension is produced in
View SolutionCompressibility of water is `5 xx 10^(-10) m^(2) N^(-1)`. The change in volume of 100 mL water subjected to `15 xx 10^(6)` Pa pressure will be
View SolutionA wire elongates by `l` mm when a load W is hanged from it. If the wire goes over a pulley and two weights W each are hung at the two ends, the elongation of the wire will be (in mm)
View SolutionAn iron bar of length I and having a cross-section area A is heated from `0^(@)` to `100^(@)C`. If this bar is so held that it is not permitted to expand or bend, the force that is developed, is
View SolutionThe relation between Y (Young's modulus), K (bulk modulus) and `eta` (shear modulus) is
View SolutionWhen the tension in a metal wire is `T_(1)`, its length is `l_(1)`. When the tension is `T_(2)`, its length is `l_(2)`. The natural length of wire is
View SolutionA rubber rope of length 8 m is hung from the ceiling of a room. What is the increases in length of the rope due to its own weight? (Given, Young's modulus of elasticity of rubber `= 5 xx 10^(6) Nm^(-2)` and density of rubber `= 1.5 xx 10^(6) kg m^(-3)` and `g = 10 ms^(-2)`)
View SolutionA and B are two wire. The radius of A is twice that of B. If they are stretched by the same load, then the stress on B is
View SolutionTwo wires, one made of copper and other of steel are joined end the end (as shown in figure). The area of cross-section of copper wire is twice that of steel wire.
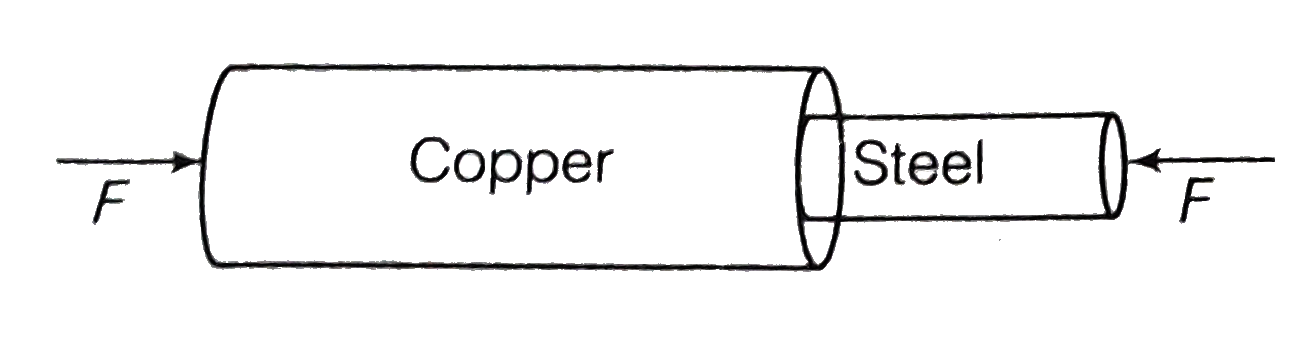
They are placed under compressive force fo magnitudes F. The ratio for their lengths such that change in lengths of both wires are same is (Given, `Y_(s) = 2 xx 10^(11) Nm^(-2)` and `Y_(C ) = 1.1 xx 10^(11) Nm^(-2)`)
View SolutionIf the Young's modulus of the material is 3 times its modulus of rigidity then its bulk modulus of elasticity will be
View SolutionIf the compressibility of water is `sigma` per unit atmospheric pressure, then the decrease in volume V due to atmospheric pressure P will be
View SolutionA cube is compressed at `0^(@)C` equally from all sides by an external pressure p. By what amount should be temperature be raised to bring it back to the size it had before the external pressure was applied? Given, B is bulk modulus of elasticity of the material of the cube and `alpha` is the coefficient of linear expansion.
View SolutionThe compressibility of water is `4xx10^-5` per unit atmospheric pressure. The decrease in volume of 100 cubic centimetre of water under a pressure of 100 atmosphere will be
View SolutionA wire is suspended by one end. At the other end a weight equivalent to 20 N force is applied. If the increase in length is 1.0 mm, the increase in energy of the wire will be
View SolutionYoung's modulus of the material of a wire is Y. ON pulling the wire by a force F, the increase in its length is x. The potential energy of the stretched wire is
View SolutionA 1 m long steel wire of cross-sectional area `1 mm^(2)` is extended 1 mm. If `Y = 2 xx 10^(11) Nm^(-2)`, then the work done is
View SolutionTwo wire of same material and same diameter have lengths in the ratio 2 : 5. They are stretched by same force. The ratio of work done in stretching them is
View SolutionIf in a wier of Young's modulus Y, longitudinal strain X is produced, then the value of potential energy stored in its unit volume will be
View SolutionA wire suspended vertically from one of the its ends is stretched by attaching a weight of 200 N to the lower end. The weight stretches the wire by 1 mm. then the elastic energy stored in the wire is
View SolutionA body of mass m = 10 kg is attached to a wire of length 0.3m. The maximum angular velocity with which it can be rotated in a horizontal circle is (Given, breaking stress of wire `= 4.8 xx 10^(7) Nm^(-2)` and area of cross-section of a wire `= 10^(-2) m^(2)`)
View SolutionTwo wires of equal lengths and cross-sections are suspended as shown in the figure. Their Young's moduli are `y_(1)` and `y_(2)` respectively. What is their equivalent Young's modulus?

View SolutionTwo cylinders of same material and of same lengths are joined to end as shown in the figure. The upper end of A is rigidly fixed. Their radii are in ratio of 1 : 2. If the lower end of B is twisted by an angle `theta`, then the angle of twist of cylinder A is
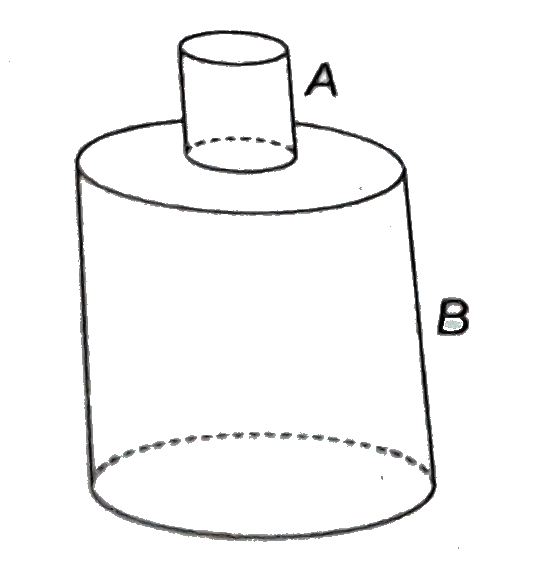
View SolutionWires A and B are made from the same material. A has twice the diameter and three times the length of B. If the elastic limits are not reached, when each is stretched by the same tension, the ratio of energy stored in A to that in B is.
View SolutionTwo wires of the same material and length but diameters in the ratio 1 : 2 are stretched by the same force. The potential energy per unit volume for the two wire when stretched will be in the ratio
View SolutionA metal rod of Young's modulus `2 xx 10^(10) Nm^(-2)` undergoes elastic strain of 0.06%. The energy per unit volume stored (in `Jm^(-3)`) is
View SolutionA 45 kg boy whose leg bones are `5 cm^(2)` in area and 50 cm long falls through a height of 2m without breaking his leg bones. If the bones can stand a stress of `0.9 xx 10^(8) Nm^(-2)`, then young's modulus for the material of the bone 18
View SolutionTwo wires A and B of same length and of the same material have the respective radii `r_(1)` and `r_(2)`. Their one end is fixed with a rigid support, and at other end equal twisting couple is applied. Then the ratio of the angle of twist at the end of A and the angle of twist at the end of B will be
View SolutionIf the work done in stretching a wire by 1 mm is 2J, then work necessary for stretching another wire of same material but with double radius of corss-section and half the length by 1 mm is
View SolutionIn above question, the work done in the two wire is
View SolutionA material has Poisson's ratio `0.50`. If a uniform rod of it suffers a longitudinal strain of `2 xx 10^(-3)`, then the percentage change in volume is
View SolutionA rigid bar of mass M is supported symmetrically by three wires each of length I. Those at each end are of copper and the middle one is of iron. What is the ratio of their diameters `(D_("copper"))/(D_("iron"))` if each wire is to have ratio same tension?
View SolutionWhen a wire is subjected to a force along its length, its length increases by 0.4% andits radius decreaes by 0.2%. Then, the poisson's ratio of the material of the wire is
View SolutionTwo rods of different materials with coefficients linear thermal expansion `alpha_(1), alpha_(2)`, and Young's moduli `Y_(1)` and `Y_(2)`, respectively are fixed between two rigid walls. They are heated to have the same increase in temperature . If the rods do not bend and if `alpha_(1) : alpha_(2) = 2 : 3`, then thermal stresses developed in the two rods will be equal when `Y_(1) : Y_(2)` ie equal to
View SolutionIf longitudinal strain for a wire is 0.03 and its Poisson's ratio is 0.5, then its lateral strain is
View SolutionThe poisson's ratio cannot have the value
View Solution
EXERCISE 1 questions and complete solutions for chapter ELASTICITY of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12