Complete Solutions to Exercise 2 of chapter WAVE MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE MOTION |
| MHTCET PREP GUIDE | Exercise 2 |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
The displacement x(in metres) of a particle performing simple harmonic motion is related to time t(in seconds) as `x=0.05cos(4pit+(pi)/4)` .the frequency of the motion will be
View SolutionWave of frequency 500 Hz has a phase velocity `360 m//s`. The phase difference between two displacement at a certain point at time `10^(-3)s` apart will be
View SolutionIf the speed of a wave doubles as it passes from shallow water into deeper water, its wavelength will be
View SolutionAn observer is approaching a stationary source with a velocity `1/4` th of the velocity of sound. Then the ratio of the apparent frequency to actual frequency of source is
View SolutionThe resultant wave obtained when the above two waves interfere with each other is best represented as

View SolutionThe temperature at which the speed of sound in air becomes double of its value at `27^(@)C` is
View SolutionA sine wave has an amplitude A and wavelength `lambda`. Let V be the wave velocity and v be the maximum velocity of a particle in the medium. Then
View SolutionTwo waves represented by `y=asin(omegat-kx)` and `y=acos(omegat-kx)` are superposed. The resultant wave will have an amplitude.
View SolutionA travelling wave in a stretched string is described by the equation `y = A sin (kx - omegat)` the maximum particle velocity is
View SolutionWhen two progressive waves `y_(1) = 4 sin (2x - 6t)` and `y_(2) = 3 sin (2x - 6t - (pi)/(2))` are superimposed, the amplitude of the resultant wave is
View SolutionSound waves of `v=60 Hz` fall normally on a perfectly reflecting wall. The shortest distance from the wall at which all particles will have maximum amplitude of vibration will be (Given, speed of sound `=300 ms^(-1)`)
View SolutionThe equation of a wave on a string of linear mass density `0.04 kg m^(-1)` is given by `y = 0.02 (m) sin [2pi((t)/(0.04(s))-(x)/(0.50(m)))]`. The tension in the string is :
View SolutionThe displacement `y` of a particle executing periodic motion is given by `y = 4 cos^(2) ((1)/(2)t) sin(1000t)`
This expression may be considereed to be a result of the superposition of
View SolutionA progressive wave y = A sin (k x - `omega`t) is reflected by a rigid wall at x = 0 . Then the reflected wave can be represented by -
View SolutionA fork of unknown frequency gives 4 beats per second when sounded with another of frequency `256`. The fork is now loaded with a piece of wax and again 4 beats per second are heard. Calculate the frequency of the unknown fork.
View SolutionBeast are produced by frequencies `v_(1)` and `v_(2) (v_(1) gt v_(2))`. The duration of time between two sucessive maximum or minima is equal to
View SolutionTwo turning forks of frequencies `n_(1)` and `n_(2)` produces n beats per second. If `n_(2)` and n are known, `n_(1)` may be given by
View SolutionA tuning fork of frequency 480 Hz produces 10 beats per second when sounded with a vibrating sonometer string. What must have been the frequency of the string if a slight increase in tension produces lesser beats per second than before
View SolutionTwo sitar strings A and B are slightly out of tune and produce beats of frequency 5 Hz. When the tension in the string B is slightly increased, the beat frequency is found to reduce to 3 Hz. If the frequency of string A is 427 Hz, the original frequency of string B is
View SolutionTwo tunning forks A and B produce notes of frequencies 256 Hz & 262 Hz respectively. An unknown note sounded at the same time with A produce beats. When the note is sounded with B, beats frequency is twice as large. The unknown frequency could be
View SolutionA source of sound gives five beats per second when sounded with another source of frequency `100s^-1`. The second harmonic of the source together with a source of frequency `205s^-1` gives five beats per second. What is the ferquency of the source?
View SolutionWhen two tuning forks (fork `1` and fork `2` ) are sounded simultaneously, `4` beats per second are heard. Now, some tape is attached on the prong of the fork `2`. When the tuning forks are sounded again, `6` beats per second are heard. If the frequency of fork `1` is `200 Hz`, then what was the original frequency of fork `2` ?
View SolutionTwo sound sources emitting sound each of wavelength `lambda` are fixed at a given distance apart. A listener moves with a velocity `u` along the line joining the two suorces. The number of beats heard by him per second is
View SolutionA source of sound of frequency 256 Hz is moving towards a wall with a velocity of 5 m/s. How many beats per second will be heard by an observer O standing in such a positoin that the source S is between O and wall? `(c=330(m)/(s))`
View SolutionA bus is moving with a velocity of `5 ms^(-1)` towards a huge wall. The driver sound a horn of frequency 165 Hz. If the speed of sound in air is `335 ms^(-1)`, the number of beats heard per second by a passenger inside the bus will be
View SolutionA sound wave of frequency `f` travels horizontally to the right. It is reflected from a large vertical plane surface moving to left with a speed `v`. The speed of sound in medium is `C`
View SolutionThe equation of a wave travelling on a string is `y=8 sin [pi/2 (4t-x/16)]`, where x, y are in cm and t in second. The velocity of the wave is
View SolutionThe diagram shows the propagation of a progressive wave A, B, C, D, E, are five points on this wave.
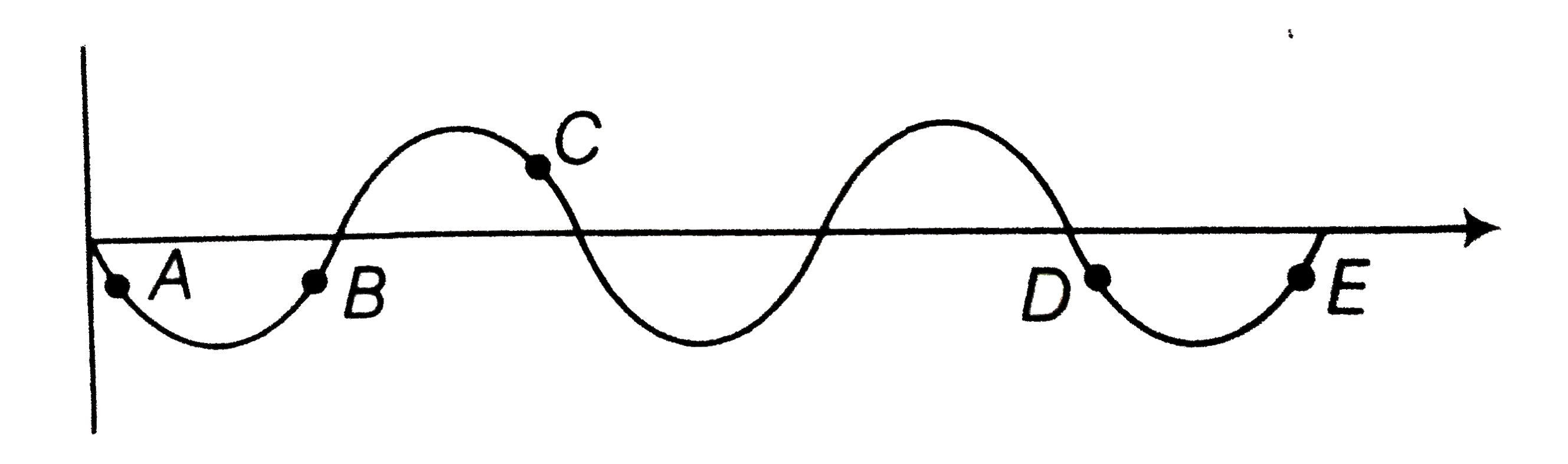
Which points are in the same state of vibration?
View SolutionIf the amplitude of a wave at a distance `r` from a point source is `A`, the amplitude at a distance `2 r` will be
View SolutionThe equation of a progresive wave along a string is `y=2 x 10^(-6) sin pi (t/0.002-x/60)` where x is in cm and t is in second. What is the phase difference at any instant between two points which are 2 cm apart?
View Solution
Exercise 2 questions and complete solutions for chapter WAVE MOTION of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12