Complete Solutions to Exercise 1 (TOPICAL PROBLEMS) of chapter INTERFERENCE AND DIFFRACTION OF LIGHT of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | INTERFERENCE AND DIFFRACTION OF LIGHT |
| MHTCET PREP GUIDE | Exercise 1 (TOPICAL PROBLEMS) |
| Number Of Questions | 53 |
| Academic Year | 2023-24 |
A is an essential condition for coherent sources. Here, A refers to
View SolutionThe maximum intensity of fringes in Young's experiment is I. If one of the slit is closed, then the intensity at that place becomes `I_o`. Which of the following relation is true?
View SolutionThe maximum intensity in the case of n identical waves each of intensity `2(W)/(m^(2))` is `32(W)/(m^(2))` the value of n is
View Solution`S_(1) and S_(2)` are two coherent sources. The intensity of both sources are same. If the intensity at the point of maxima is `4Wm^(-2)`, the intensity of each source is
View SolutionThree waves of equal frequency having amplitudes `10mum`, `4mum`, `7mum` arrive at a given point with successive phase difference of `pi//2`, the amplitude of the resulting wave in `mum` is given by
View SolutionA parallel beam of light of intensity I is incident on a glass plate. `25%` of light is reflected in any reflection by upper surface and `50%` of light is reflected by any reflection from lower surface. Rest is refracted The ratio of maximum to minimum intensity in interference region of reflected rays is

View SolutionTwo periodic waves of intensities `I_(1)` and `I_(2)` pass through a region at the same time in the same direction. The sum of the maximum and minimum intensities is:
View SolutionInterference was observed in interference chamber when air was present, now the chamber is evacuated and if the same light is used, a careful observer will see
View SolutionTwo coherent monochromatic light beams of intensities I and 4I are superposed. The maximum and minimum possible intensities in the resulting beam are
View SolutionTwo coherent monochormatic light source are located at two vertices of an equilateral trangle. If the intensity due to each of the source independently is `1Wm^(-2)` at the third vertex. The resultant intensity due to both the sources at that point (i.e at the third vertex) is (in `Wm^(-2)` )
View SolutionTwo coherent waves are represented by `y_(1)=a_(1)cos_(omega)` t and `y_(2)=a_(2)sin_(omega)`t. The resultant intensity due to interference will be
View SolutionTwo sources are called coherent if they produce waves
View SolutionThe ratio of the intensities of two waves is `16:9`. The ratio of their amplitudes is
View SolutionMatch the following columns and choose the correct options from the codes given below.

View SolutionThe Young's double slit experiment is performed with blue and with green light of wavelengths `4360 A` and `5460 A` respectively. If `X` is the distance of `4th` maximum from the central one, then :
View SolutionIn Young's experiment, the wavelength of red light is `7.8xx10^(-5)` cm and that of blue light is `5.2 xx 10^(-5)` cm. The value of n for which (n + 1)th blue light band coincides with nth red band is
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionIn the setup shown in figure, the two slits, `S_(1)` and `S_(2)` are not equidistant from the slit S. The central fringe at O is, then
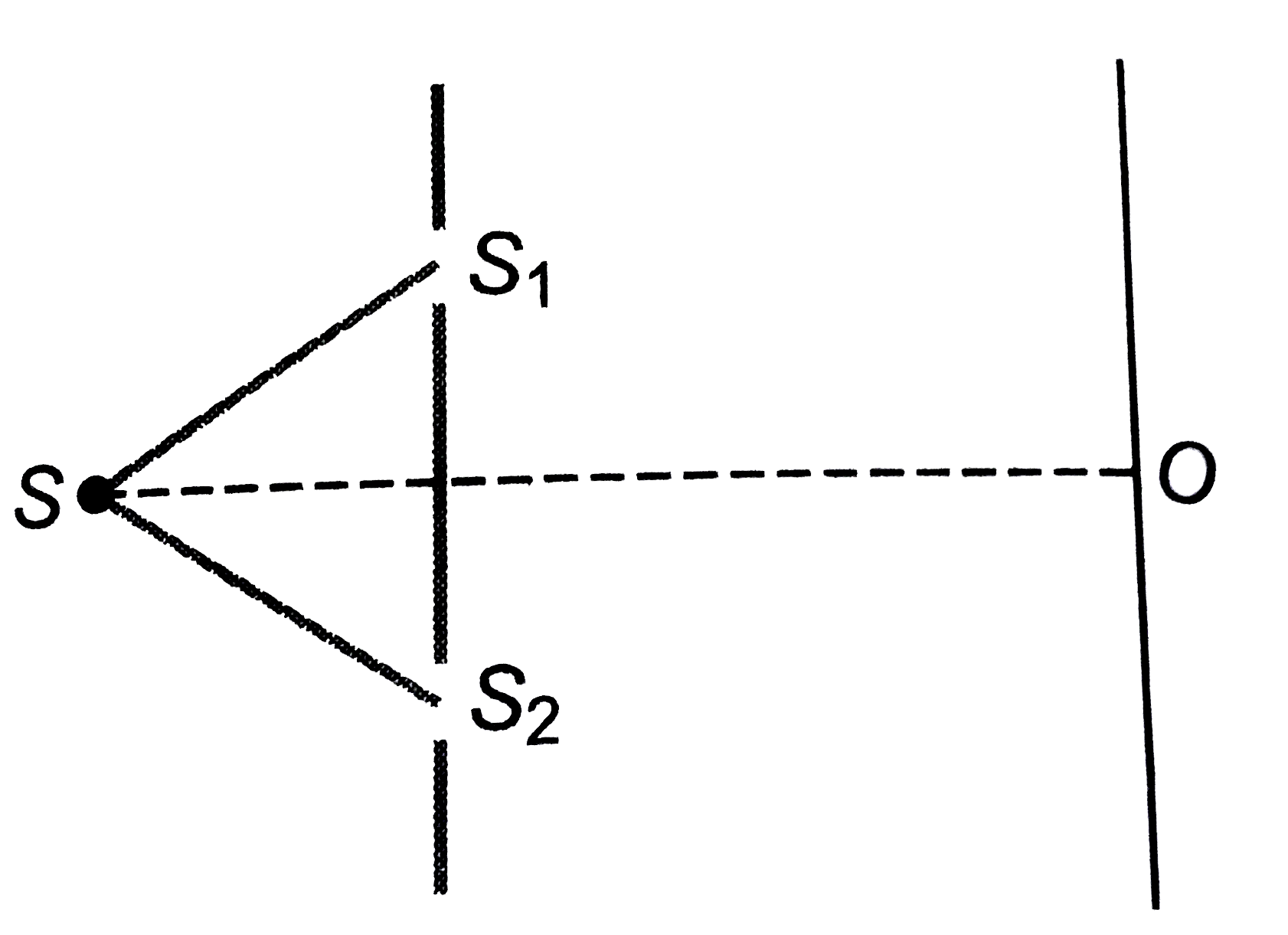
View SolutionThe separation between successive fringes in a double slit arrangement is x. If the whole arrangement is dipped under water, what will be the new fringe separation ? [The wavelength of light being used is `5000 Å`]
View SolutionIn a Young's double-slit experiment, let `S_(1)` and `S_(2)` be the two slits, and `C` be the centre of the screen. If `/_S_(1)CS_(2)=theta` and `lambda` is wavelength, the fringe width will be
View SolutionIn the Young's double slit experiment , a mica slip of thickness t and refractive index `mu` is introduced in the ray from first source `S_(1)` . By how much distance fringes pattern will be displaced ? (d = distance between the slits and D is the distance between slits and screen)
View SolutionIn double slit experiment, the angular width of the fringes is `0.20^@` for the sodium light `(lambda=5890Å)`. In order to increase the angular width of the fringes by `10%`, the necessary change in the wavelength is
View SolutionA beam of light consisting of two wavelength `650nm` and `520nm` is used to illuminate the slit of a Young's double slit experiment. Then the order of the bright firnge of the longer wavelength that coincide with a bright fringe of the shorter wavelength at the least distance from the central maximum is
View SolutionIn Young's double slit experiment, the 8th maximum with wavelength `lambda_1` is at a distance `d_1` from the central maximum and the 6th maximum with a wavelength `lambda_2` is at a distance `d_2`. Then `(d_1//d_2)` is equal to
View SolutionIn a Young's experiment, two coherent sources are placed `0.90mm` apart and the fringes are observed one metre away. If is produces the second dark fringe at a distance of `1mm` from the central fringe, the wavelength of monochromatic light used would be
View SolutionThe wavelength of the light used in Young's double slit experiment is `lambda`. The intensity at a point on the screen is I, where the path difference is `(lambda)/(6)`. If `I_(0)` denotes the maximum intensity, then the ratio of I and `I_(0)` is
View SolutionIn a double slit interference experiment, the fringe width obtained with a light of wavelength 5900 Å was 1.2 mm for parallel narrow slits placed 2 mm apart. In this arrangement. If the slit separation is increased by one-and-half times the previous value, then the fringe width is
View SolutionIn an interference pattern the position of zeroth order maxima is 4.8 mm from a certain point P on the screen. The fringe width is 0.2 mm. The position of second maxima from point P is
View SolutionThe ratio of intensity at the centre of a bright fringe to the intensity at a point distant one-fourth of the distance between two successive bright fringes will be
View SolutionIn a Young's double slit experiment, the slit separation is `1mm` and the screen is `1m` from the slit. For a monochromatic light of wavelength `500nm`, the distance of 3rd minima from the central maxima is
View SolutionIn double slit experiment , the distance between two slits is `0.6mm` and these are illuminated with light of wavelength `4800 Å`. The angular width of dark fringe on the screen at a distance 120 cm from slits will be
View SolutionIn Young's double slit experiment, the aperture screen distance is `2m`. The fringe width is `1mm`. Light of `600nm` is used. If a thin plate of glass `(mu=1.5)` of thickness `0.06mm` is placed over one of the slits, then there will be a lateral displacement of the fringes by
View SolutionIn a Young's double slit experiment, the fringe width is found to be `0.4mm`. If the whole apparatus is immersed in water of refractive index `4//3` without disturbing the geometrical arrangement, the new fringe width will be
View SolutionIn young's double slit experiment, if wavelength of light changes from `lambda_(1)` to `lambda_(2)` and distance of seventh maxima changes from `d_(1)` to `d_(2)`. Then
View Solutionin a two-slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by `5xx10^(-2)` m towards the slits, the change in fringe width is `3xx10^(-5)`. If the distance between the slits is `10^(-3)`m, calculate the wavelength of the light used.
View SolutionIn Young's double slit experiment, the intensity on the screen at a point where path difference is `lambda` is K. What will be the intensity at the point where path difference is `lambda//4`?
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionIn the Young's experiment, one of the slit is covered with a transparent sheet of thickness `3.6xx10^(-3)` cm due to which position of central fringe shifts to a position originally occupied by 30th bright fringe. The refractive index of the sheet, if `lambda=6000Å` is
View SolutionA double slit experiment is performed with light of wavelength `500nm`. A thin film of thickness `2mum` and refractive index `1.5` is introduced in the path of the upper beam. The location of the central maximum will
View SolutionIn a Young's double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case
View SolutionA small aperture is illuminated with a parallel beam of `lambda = 628 nm`. The emergent beam has an anglur divergence of `2^(@)`. The size of the aperture is
View SolutionIn a single slit diffraction of light of wavelength `lambda` by a slit of width e, the size of the central maximum on a screen at a distance b is
View SolutionThe angular width of the central maximum of the diffraction patternn in a single slit (of width a) experiment, with `lamda` as the wavelenth of light, is
View SolutionA single slit Fraunhofer diffraction pattern is formed with white light. For what wavelength of light the third secondary maximum in the diffraction pattern coincides with the secondary maximum in the pattern for red light of wavelength 6500 Å ?
View SolutionIn a diffraction pattern due to single slit of width `'a'`, the first minimum is observed at an angle `30^(@)` when light of wavelength `5000 Å` is inclined on the slit. The first secondary maximum is observed at an angle of:
View SolutionA beam of light of wavelength 600 nm from a distant source falls on a single slit 1 mm wide and the resulting diffraction pattern is observed on a screen 2 m away. The distance between the first dark fringes on either side of the central bright fringe is
View SolutionIn Fraunhofer diffraction experiment, L is the distance between screen and the obstacle, b is the size of obstacle and `lambda` is wavelength of incident light. The general condition for the applicability of Fraunhofer diffraction is :
View SolutionThe distance between the first and the sixth minima in the diffraction pattern of a single slit is 0.5 mm. The screen is 0.5 m away from the slit. If the wavelength of light used is 5000 Å. Then the slit width will be
View SolutionRed light of wavelength 625 nm is incident normally on a optical diffraction grating with `2xx10^(5)` lines/m. Including central principal maxima, how many maxima may be observed on a screen which is far from the grating?
View SolutionA parallel monochromatic beam of light is incident normally on a narrow slit. A diffraction pattern is formed on a screen placed perpendicular to the direction of the incident beam. At the first minimum of the diffraction pattern, the phase difference between the rays coming from the two edges of the slit is
View SolutionThe source is at some distance from an obstacle. Distance between obstacle and the point of observation is b and wavelength of light is `lambda`. Then the average distance of nth Fresnel zone will be at a distance …from the point of observation.
View SolutionWhen a compact disc is illuminated by a source of white light, coloured lines are observed. This is due to
View SolutionWhen light is incident on a diffraction grating, the zero order principal maximum will be
View Solution
Exercise 1 (TOPICAL PROBLEMS) questions and complete solutions for chapter INTERFERENCE AND DIFFRACTION OF LIGHT of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12