Complete Solutions to प्रश्नावली 8.6 (पाठ्य पुस्तक) of chapter अवकलजों के अनुप्रयोग of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | अवकलजों के अनुप्रयोग |
| MITTAL PUBLICATION | प्रश्नावली 8.6 (पाठ्य पुस्तक) |
| Number Of Questions | 5 |
| Academic Year | 2023-24 |
सिद्ध कीजिए कि किसी वृत्त में बड़े से बड़ा त्रिभुज जो खींचा जा सकता है, वह समबाहु होगा।
View Solutionकिसी वर्ग का परिमाप तथा वृत्त की परिधि का योग दिया हुआ है। सिद्ध कीजिए कि उनके क्षेत्रफल का योग न्यूनतम होगा यदि वर्ग की भुजा वृत्त के व्यास के बराबर है।
View Solutionयदि एक गोले में एक शंकु बनाया जाता है तब सिद्ध कीजिए कि उसका आयतन महत्तम होगा यदि शंकु की ऊँचाई गोले के व्यास की दो तिहाई हो।
View Solutionयदि एक समकोण त्रिभुज के कर्ण तथा एक भुजा का योग दिया हुआ है। तब सिद्ध कीजिए कि त्रिभुज का क्षेत्रफल अधिकतम होगा। यदि इन भुजाओं के मध्य कोण `(pi)/(3)` है।
View Solutionयदि किसी समबाहु त्रिभुज के अंदर a त्रिज्या का वृत्त बनाया गया है। तब सिद्ध कीजिए कि त्रिभुज न्यूनतम परिमाप `6sqrt(3)a` होगा।
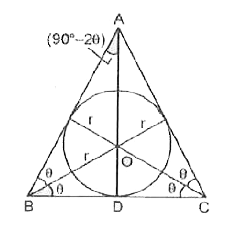
View Solution
प्रश्नावली 8.6 (पाठ्य पुस्तक) questions and complete solutions for chapter अवकलजों के अनुप्रयोग of MITTAL MATHS (HINDI) of Class 12
All Exercises from MITTAL PUBLICATION Class 12 MATHS अवकलजों के अनुप्रयोग
- CHECK YOUR POTENTIALITY
- COMPETITION CORNER
- LAST YEAR.S BOARD QUESTIONS
- PRACTICE QUESTIONS
- अभ्यासार्थ प्रश्नावली 8.1
- अभ्यासार्थ प्रश्नावली 8.2
- अभ्यासार्थ प्रश्नावली 8.3
- अभ्यासार्थ प्रश्नावली 8.4
- अभ्यासार्थ प्रश्नावली 8.5
- अभ्यासार्थ प्रश्नावली 8.6
- अभ्यासार्थ प्रश्नावली 8.7
- उदाहरण
- पाठ्य पुस्तक के उदाहरण
- प्रश्नावली 8.1 (पाठ्य पुस्तक)
- प्रश्नावली 8.2 (पाठ्य पुस्तक)
- प्रश्नावली 8.3 (पाठ्य पुस्तक)
- प्रश्नावली 8.4 (पाठ्य पुस्तक)
- प्रश्नावली 8.5 (पाठ्य पुस्तक)
- प्रश्नावली 8.6 (पाठ्य पुस्तक)
- विविध प्रश्नावली 8 (पाठ्य पुस्तक)
- साधित उदाहरण