Complete Solutions to साधित उदाहरण of chapter सदिश of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | सदिश |
| MITTAL PUBLICATION | साधित उदाहरण |
| Number Of Questions | 96 |
| Academic Year | 2023-24 |
निम्नलिखित राशियों में बताइए की कौन सदिश है तथा कौन अदिश है ?
50 सेकंड
View Solutionनिम्नलिखित राशियों में बताइए की कौन सदिश है तथा कौन अदिश है ?
`50 "मीटर"^2`
View Solutionनिम्नलिखित राशियों में बताइए की कौन सदिश है तथा कौन अदिश है ?
10 किमी /घंटा
View Solutionनिम्नलिखित राशियों में बताइए की कौन सदिश है तथा कौन अदिश है ?
30 ग्राम/सेमी^3
View Solutionनिम्नलिखित राशियों में बताइए की कौन सदिश है ?
View Solutionनिम्नलिखित राशियों में बताइए की कौन सदिश है तथा कौन अदिश है ?
5 N
View Solutionपूरब से `45^@` उत्तर में 30 km के विस्थापन का आलेखीय निरूपण कीजिए।
View Solutionदी गई आकृति (एक वर्ग) में निम्नलिखित सदिशों को पहचानिए :
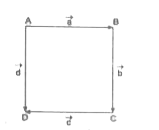
सह - आदिम
View Solutionदी गई आकृति (एक वर्ग) में निम्नलिखित सदिशों को पहचानिए :
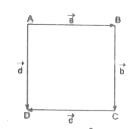
समान
View Solutionदी गई आकृति (एक वर्ग) में निम्नलिखित सदिशों को पहचानिए :

सरेख परन्तु असमान
View Solutionसदिश `4hati-5hatj+11hatk` का मापांक ज्ञात कीजिए।
View Solutionयदि सदिश `veca=2hati+4hatj-5hatk` तथा `vecb=hati+2hatj+3hatk` है तो `|veca+vecb|` का मान ज्ञात कीजिए।
View Solutionयदि `vecA=2hati-hatj+3hatk` तथा `vecB=3hati+7hatj-2hatk` तो `|2vecA-3vecB|` का मान ज्ञात कीजिए।
View Solutionयदि `veca=3hati+4hatj+5hatk` तथा `vecb=5hati+3hatj+4hatk` तब क्या `|veca|=|vecb|` ? क्या सदिश `veca` तथा `vecb` समान है ?
View Solutionसदिश `veca=2hati+hatj+3hatk` के अनुदिश मात्रक सदिश (Unit vector ) ज्ञात कीजिए।
View Solutionसदिश `veca=hati+4hatj+2hatk` के अनुदिश ऐसा सदिश ज्ञात कीजिए जिसका परिमाण 7 इकाई है।
View Solutionसदिश `veca=hati+2hatj+3hatk` के दिक् अनुपात लिखिए तथा इसकी सहायता से दिक् कोसाइन ज्ञात कीजिए।
View Solutionसदिशों `veca=5hati-2hatj+3hatk` तथा `vecb=2hati+3hatj+4hatk` के अंतर के अनुदिश मात्रक सदिश (unit vector ) ज्ञात कीजिए।
View Solutionएक सदिश का प्रारंभिक बिंदु (1,2) है तथा (-4,4) अंतिम बिंदु है। इस सदिश के अदिश एवं सदिश घटक ज्ञात कीजिए ।
View Solutionइस बिंदु का स्थिति सदिश ज्ञात कीजिए जो कि बिन्दुओ P(3,4,5) तथा Q(6,7,8) को मिलाने रेखा को 2:1 के अनुपात में (i) अंत तथा (ii) बाहा विभाजन करता है।
View Solutionबिन्दुओ A(4,3,2) तथा B(-2,1,4) को मिलाने वाले सदिश का मध्य - बिंदु ज्ञात कीजिए।
View Solutionयदि सदिश `veca,vecb,vecc` किसी त्रिभुज की भुजाओं द्वारा एक कर्म में प्रदर्शित हो , तो सिद्ध कीजिए कि सदिशों का योग सुनी सदिश होता है अर्थात `veca+vecb+vecc=vec0`
View Solutionसिद्ध कीजिए कि तीन सदिश `(5hati-2hatj-7hatk), (4hati+3hatj+2hatk)` तथा `(9hati+hatj-5hatk)` एक समकोण त्रिभुज की भुजाएँ निर्धारत करते है।
View Solutionसदिशों `2hati+3hatj-6hatk, 6hati-2hatj+3hatk` तथा `3hati+6hatj-2hatk` द्वारा क्या एक समबाहु त्रिभुज बनता है ?
View Solutionयदि एक सदिश OX , OY और OZ अक्षो से क्रमश: `alpha , beta ` और `gamma` कोण बनता है , तो सिद्ध कीजिए कि `sin^2alpha +sin^2beta+sin^2gamma=2`
View Solutionयदि `veca=2hati+2hatj-hatk` तथा `vecb=6hati-3hatj+2hatk` तो `veca.vecb` का मान ज्ञात कीजिए।
View Solutionसदिशों `veca=4hati+3hatj+hatk vecb=2hati-hatj+2hatk` के बीच का कोण ज्ञात कीजिए।
View Solutionयदि `veca=2hati+3hatj+3hatk, vecb=-hati+2hatj+hatk,vecc=3hati+hatj` तथा `veca+lambda vecb` सदिश `vecc` पर लम्ब हो , तो `lambda` का मान ज्ञात कीजिए।
View Solutionसदिश `7hati+3hatj+hatk` का सदिश `8hati-hatj+7hatk` पर प्रक्षेप ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि बिंदु जिनके स्थिति सदिश क्रमश: `2hati-hatj+hatk,hati-3hatj-5hatk` तथा `3hati-4hatj-4hatk` है , एक समकोण त्रिभुज के शीर्ष है।
View Solutionसिद्ध कीजिए कि सदिश `veca=hati+2hatj+hatk, vecb=hati+hatj-3hatk` तथा `vecc=7hati-4hatj+hatk` एक-दूसरे पर लम्ब है।
View Solutionयदि `veca` तथा `vecb` दो सदिश है जिनके परिमाण (मापांक ) क्रमश: a और b है , तो सिद्ध कीजिए कि `(veca/a_2-vecb/b^2)^2=((veca-vecb)/(ab))^2` `|veca|=a` तथा `|vecb|=b`
View Solutionयदि सदिश `veca` तथा `vecb` इस प्रकार है कि `|veca|=3` तथा `|vecb|=4` तथा `veca.vecb=5`, तो `|veca - vecb|` ज्ञात कीजिए।
View Solutionयदि सदिश `veca` मात्रक सदिश है तथा `(vecx-veca). (vecx+veca)=15`, तो `|vecx|` का मान ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि दो सदिशों `veca` तथा `vecb` के लिए सदैव (त्रिभुज असमीका ) `|veca+vecb| le |veca|+|vecb|` सत्य होता है।
View Solutionयदि `triangleABC` के शीर्ष कोणों की सम्मुख भुजाएँ क्रमश: a,b तथा c हो , तो सिद्ध कीजिए कि `cosC=(a^2+b^2-c^2)/(2ab)`
View Solutionसिद्ध कीजिए कि अर्धवृत्त में स्थित कोण समकोण होता है।
View Solutionयदि `veca=2hati-hatj+hatk` तथा `vecb=hati+hatj-3hatk` तो `vecaxxvecb` ज्ञात कीजिए ।
View Solutionयदि `veca=2hati+hatj+7hatk` तथा `vecb=hatj+6hatk` तो `vecaxxvecb` का मान ज्ञात कीजिए ।
View Solutionसदिशों `veca=2hati-hatj+hatk` और `vecb=3hati+4hatj-hatk` के बीच के कोण की ज्या (sin) ज्ञात कीजिए।
View Solutionयदि `veca=hati+2hatj+3hatk` और `vecb=3hati-2hatj+2hatk`, तो `veca` और `vecb` दोनों के लंबवत एकांक सदिश ज्ञात कीजिए।
View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिनके शीर्ष A(1,-1,2) ,B(2,1,-1) तथा C(3,-1,2) है।
View Solutionउस समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी आसन्न भुजाएँ `veca=hati+2hatj+3hatk` तथा `vecb=3hati-2hatj+hatk` है।
View Solutionयदि सदिश `veca` और `vecb` इस प्रकार है कि `|veca|=3` और `|vecb|=sqrt2/3` , यदि `vecaxxvecb` एक इकाई सदिश है , तो `veca` और `vecb` के बीच का कोण ज्ञात कीजिए।
View Solutionयदि `veca+vecb+vecc=vec0` तो सिद्ध कीजिए कि `vecaxxvecb=vecbxxvecc=veccxxveca`.
View Solutionयदि `|veca|=7, |vecb|=sqrt26` और `|vecaxxvecb|` =35 ,तो `veca.vecb` ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि `hatixx(vecaxxhati)+hatjxx(vecaxxhatj)+hatkxx(vecaxxhatk)=2veca`
View Solutionयदि `veca=hati+hatj-hatk,vecb=2hati+hatj+2hatk` और `vecc=3hati+hatj+3hatk` ,तो `veca.(vecbxxvecc)` का मान ज्ञात कीजिए।
View Solutionउस समांतर षट्फलक का आयतन ज्ञात कीजिए जिसकी भुजाएँ `veca=2hati+3hatj+4hatk,vecb=hati+2hatj-hatk` और `vecc=3hati-hatj+2hatk` है।
View Solutionसिद्ध कीजिए कि सदिश `hati+2hatj+5hatk, hati-hatj+2hatk` और `hati-2hatj+hatk` एक समतलीय है।
View Solution'm'' का वह मान ज्ञात कीजिए जिसके लिये सदिश `veca=hati-hatj+hatk,vecb=2hati+hatj-hatk` और `vecc=mhati-hatj+mhatk` एक समतलीय है।
View Solutionसिद्ध कीजिए कि चार बिंदु A,B,C और D जिनके निर्देशांक क्रमश: (4,5,1),(0,-1,-1),(3,9,4) और (-4,4,4) है ,एक समतलीय है।
View Solutionयदि `vecl=ahati+hatj+hatk, vecm=hati+bhatj+hatk` तथा `vecn=hati+hatj+hatk` एकसमतलीय है तो सिद्ध कीजिए कि `1/(1-a)+1/(1-b)+1/(1-c)=1`, जहाँ `a ne 1, b ne 1 , c ne 1`
View Solutionयदि `veca,vecb,vecc` परस्पर लम्बकोणीय सदिश है, तो सिद्ध कीजिए कि
`[veca,vecb,vecc]^2=a^(2)b^(2)c^(2)`.
View Solutionयदि `veca=3hati-4hatj-hatk,vecb=2hati+hatj+hatk` तथा `vecc=hati-2hatj+4hatk` है तो `{vecaxx(vecbxxvecc)}` का मान ज्ञात कीजिए।
View Solutionयदि `veca=-2hati+3hatj-4hatk,vecb=hati-2hatj+3hatk` तथा `vecc=hati-3hatj+5hatk` है तो `{(vecaxxvecb)xxvecc}` का मान ज्ञात कीजिए।
View Solutionसूत्र `vecaxx(vecbxxvecc)=(veca.vecc)vecb-(veca.vecb)vecc` को सत्यापित कीजिए जबकि `veca=hati-2hatj+hatk, vecb=2hati+hatj+hatk` तथा `vecc=hati+2hatj-hatk`
View Solutionयदि `[vecavecbvecc]ne0` है तो सिद्ध कीजिए कि सदिश `(vecaxxvecb),(vecbxxvecc)` तथा `(veccxxveca)` एकसमतलीय नहीं है
View Solutionसिद्ध कीजिए कि सदिश `(veca+vecb),(vecb+vecc)` तथा `(vecc+veca)` एक समतलीय होंगे , यदि और केवल यदि `(vecaxxvecb),(vecbxxvecc)` तथा `(veccxxveca)` एक समतलीय है।
View Solutionसिद्ध कीजिए कि `[vecaxxvecb vecaxxvecc vecd]=[veca.vecd][veca vecb vecc]`
View Solutionसिद्ध कीजिए कि `(vecaxxvecb).(veccxxvecd)=(veca.vecc)(vecb.vecd)-(veca.vecd)(vecb.vecc)`
View Solutionयदि `veca,vecb,vecc,vecd` समतलीय सदिश है तो सिद्ध कीजिए कि `(vecaxxvecb)xx(veccxxvecd)=vec0`
View Solutionसदिशों `veca=hati-2hatj+hatk,vecb=-2hati+4hatj+5hatk` तथा `vecc=hati-6hatj-7hatk` का योगफल ज्ञात कीजिए।
View Solutionयदि सदिश `veca=xhati+2hatj+zhatk` और `vecb=2hati+yhatj+hatk` समान है , तो x,y व z के मान ज्ञात कीजिए ।
View Solutionमान लीजिए `veca=hati+2hatj` और `vecb=2hati+hatj` तब क्या `|veca||vecb|` है ? क्या सदिश `veca` और `vecb` समान है ?
View Solutionसदिश `veca=2hati+3hatj+hatk` के अनुदिश मात्रक सदिश ज्ञात कीजिए।
View Solutionसदिश `veca=hati-2hatj` के अनुदिश एक ऐसा सदिश ज्ञात कीजिए जिसका परिमाण 7 इकाई है।
View Solutionसदिश `veca=2hati+2hatj-5hatk` और `vecb=2hati+hatj+3hatk` के योगफल के अनुदिश सदिश ज्ञात कीजिए।
View Solutionसदिश `veca=hati+hatj-2hatk` के दिक् - अनुपात लिखिए और इसकी सहायता से दिक् - कोसाइन ज्ञात कीजिए ।
View Solutionबिंदु P(2,3,0) एवं Q(-1,-2,-4) को मिलाने वाला एवं P से Q की तरफ दिष्ट ज्ञात कीजिए।
View Solutionदो बिंदु P और Q के स्थिति सदिश क्रमश: `vec(OP)=3veca-2vecb` और `vec(OQ)=veca+vecb` है। एक ऐसे बिंदु R का स्थिति सदिश ज्ञात कीजिए , जो P एवं Q को मिलाने वाली रेखा को के 2:1 अनुपात में अन्तः बाहा विभाजित करता है।
View Solutionदर्शाइए कि बिंदु `A(2hati-hatj+hatk),B(hati-3hatj-5hatk), C(3hati-4hatj-4hatk)` एक समकोण त्रिभुज के शीर्ष है।
View Solutionयदि `veca=hati+2hatj+3hatk` तथा `vecb=3hati+2hatj+hatk` हो तो `veca.vecb` का मान ज्ञात कीजिए।
View Solution`lambda` के किस मान के लिए सदिश `2hati+lambdahatj+5hatk` और `-hati+hatj+hatk` परस्पर लंबवृत है।
View Solutionसदिश `3hati+hatj+3hatk` तथा `2hati+2hatj-hatk` के मध्य का कोण ज्ञात कीजिए।
View Solutionप्रदर्शित कीजिए कि `(veca+vecb)^2=a^2+2a.b+b^2`
View Solutionप्रदर्शित कीजिए कि `(veca.vecb).(veca-vecb)=a^2-b^2`
View Solutionयदि दो इकाई सदिशों `veca` और `vecb` के मध्य का कोण `theta` है , तो सिद्ध कीजिए कि `"sin" theta/2 =1/2[hata-hatb]`.
View Solutionयदि `veca,vecb,vecc` समान परिमाण के परस्पर लम्ब सदिश हो तो सिद्ध कीजिए कि सदिश `veca+vecb+vecc` सदिशों `veca,vecb` और `vecc` के साथ बराबर कोण बनाता है।
View Solution`veca,vecb,vecc` क्रमश: 3,4,5 परिमाण के सदिश है। यदि प्रत्येक सदिश अन्य दो सदिशों के योग पर लम्ब हो , तो सदिश `veca+vecb+vecc` का परिमाण ज्ञात कीजिए।
View Solution`(2hati-3hatj+4hatk)xx(3hati+4hatj-4hatk)` का मान ज्ञात कीजिए।
View Solutionयदि `veca=3hati+hatj+2hatk` तथा `vecb=2hati-2hatj+2hatk` हो तो `veca` तथा `vecb` दोनों के लंबवृत इकाई सदिश `hatn` ज्ञात कीजिए।
View Solutionयदि `vecaxxvecb=veccxxvecd` तथा `vecaxxvecc=vecbxxvecd`, तो सिद्ध कीजिए कि `veca-vecd` एवं `vecb-vecc` समान्तर है।
View Solutionयदि `vecaxxvecb=veccxxvecb`तो सिद्ध कीजिए `veca-vecc = lambdavecb` कि जहाँ एक `lambda` अदिश है।
View Solutionयदि A(1,2,2),B(2,-1,1) तथा C(-1,2,3) समतल में कोई तीन बिंदु हो तो समतल ABC के अभिलम्ब कि दिशा में एक सदिश ज्ञात कीजिए जिसका परिमाण 5 इकाई है।
View Solutionसिद्ध कीजिए कि समान्तर चतुर्भुज ABCD का क्षेत्रफल `1/2|vec(AC)xxvec(BD)|` द्वारा व्यक्त होता है , जहाँ `vec(AC)`तथा `vec(BD)` इसके विकर्ण है।
View Solutionसिद्ध कीजिए कि `[hatihatjhatk]+[hatjhatkhati]+[hatkhatihatj]=3`
View Solutionयदि `veca=hati-2hatj+hatk,vecb=hati+hatj+hatk` तथा `vecc=hati+2hatj+hatk` हो ,तो `veca.(vecbxxvecc)` तथा `(vecaxxvecb).vecc` का मान ज्ञात कीजिए। दर्शाइए कि `veca.(vecbxxvecc)=(vecaxxvecb).vecc`
View Solutionसिद्ध कीजिए कि `[veca+vecb vecb+vecc vecc+veca]=2[veca vecb vecc]`
View Solution`lambda` के किस मान के लिए सदिश `veca=2hati-hatj+hatk,vecb=hati+2hatj-3hatk` और `vecc=3hati+lambdahatj+5hatk` समतलीय होंगे ।
View Solutionसिद्ध कीजिए कि बिंदु A(4,8,12),B(2,4,6),C(3,5,4),D(5,8,5) समतलीय है।
View Solutionयदि चार बिंदु `A(veca),B(vecb),C(vecc)` एवं `D(vecd)` समतलीय हो तो सिद्ध कीजिए कि `[vecavecbvecc]=[vecbveccvecd]+[veccvecavecd]+[vecavecbvecd]`
View Solutionउस समान्तर षट्फलकी का आयतन ज्ञात कीजिए जिसकी तीन संगामी कोरे `2hati-3hatj+4hatk,hati+2hatj-hatk` तथा `2hati-hatj+2hatk` है।
View Solutionएक चतुष्फलक के चारो शीर्ष O(0,0,0), A(1,2,1),B(2,1,3) और C(-1,1,2) है चतुफलक का आयतन ज्ञात कीजिए।
View Solutionयदि `veca=3hati+2hatj+hatk, vecb=hati-2hatj+2hatk` तथा `vecc=2hati+hatj-hatk` हो , तो `vecaxx(vecbxxvecc)` का मान ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि `(vecaxxvecb)xxvecc=vecaxx(vecbxxvecc)` यदि और केवल यदि `(veccxxveca)xxvecb=vec0`
View Solution
साधित उदाहरण questions and complete solutions for chapter सदिश of MITTAL MATHS (HINDI) of Class 12
All Exercises from MITTAL PUBLICATION Class 12 MATHS सदिश
- CHECK YOUR POTENTIALITY
- COMPETITION CORNER
- LAST YEAR.S BOARD QUESTIONS
- PRACTICE CORNER
- प्रश्नवाली 13.1
- प्रश्नवाली 13.1 (पाठ्य पुस्तक )
- प्रश्नवाली 13.2
- प्रश्नवाली 13.2 (पाठ्य पुस्तक )
- प्रश्नवाली 13.3
- प्रश्नवाली 13.3 (पाठ्य पुस्तक )
- प्रश्नवाली 13.4
- प्रश्नवाली 13.4 (पाठ्य पुस्तक )
- प्रश्नवाली 13.5
- प्रश्नवाली 13.5 (पाठ्य पुस्तक )
- साधित उदाहरण