Complete Solutions to पाठ्य पुस्तक के उदाहरण of chapter प्रायिकता एवं प्रायिकता बंटन of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | प्रायिकता एवं प्रायिकता बंटन |
| MITTAL PUBLICATION | पाठ्य पुस्तक के उदाहरण |
| Number Of Questions | 54 |
| Academic Year | 2023-24 |
यदि `P(A) = 6/ 11, P (B) = 5/11` और`P (A cup B) = 7/11` हो , तो ज्ञात कीजिए -
`P(A cap B)`
View Solutionयदि `P(A) = 6/ 11, P (B) = 5/11` और`P (A cup B) = 7/11` हो , तो ज्ञात कीजिए -
`P(A/B)`
View Solutionयदि `P(A) = 6/ 11, P (B) = 5/11` और`P (A cup B) = 7/11` हो , तो ज्ञात कीजिए -
`P(B/A)`
View Solutionएक प्रशिक्षक के पास 300 सत्य / असत्य प्रकार के आसान प्रश्न ,200 सत्य / असत्य प्रकार के कठिन प्रश्न ,500 बहु विकल्पीय प्रकार के आसान प्रश्न तथा 400 बहु - विकल्पीय प्रश्न के कठिन प्रश्नो का संग्रह है । यदि प्रश्नो के संग्रह में से एक प्रश्न यादृच्छया चुना जाये तो इस प्रशकन के आसान होने कि प्रैकटा ज्ञात करो यदि यह ज्ञात है कि प्रश्न बहु - विकल्पीय प्रश्न है ?
View Solutionएक सिक्के को तीन बार उछाला गया है। निम्न प्रत्येक अवस्था में `P (A/B)` ज्ञात करो -
A : तीसरी उछाल पर चित , B : पहली दोनों उछालो पर चित
View Solutionएक सिक्के को तीन बार उछाला गया है। निम्न प्रत्येक अवस्था में `P (A/B)` ज्ञात करो -
A : कम - से - कम दो चित , B : अधिकतम दो चित
View Solutionएक सिक्के को तीन बार उछाला गया है। निम्न प्रत्येक अवस्था में `P (A/B)` ज्ञात करो -
A : अधिकतम दो पट, B : कम से कम एक पद
View Solutionएक काले तथा लाल पासे को कर्म में उछाला गया है। तब
पासो पर प्राप्त अंको का योग 9 से अधिक होने कि सप्रतिबन्ध प्रायिकता ज्ञात करो यदि ज्ञात है कि काले पासे पर अंक 5 प्रकट हुआ है।
View Solutionएक काले तथा लाल पासे को कर्म में उछाला गया है। तब
पासो पर प्राप्त अंको का योग 8 होने कि सप्रतिबंध प्रायिकता ज्ञात करो यदि यह ज्ञात है कि लाल पासे पर प्रकट अंक 4 से कम है।
View Solutionएक पासे को तीन बार उछाला गया है इस प्रयोग से संबंधित घटनाओ A व B को निम्न प्रकार परिभाषित किया गया है :
A : तीसरी उछाल पर अंक 4 का प्रकट होना
B : पहली दो उछालो पर क्रमशः6 तथा 6 प्रकट होना इस अवस्था में `P(A/B)`ज्ञात करो।
View Solutionएक पासे को उछालने के परीक्षण पर विचार कीजिए। यदि पासे पर प्राप्त अंक 3 या 3 का गुणज हो , तो पासे का पुनः उछाला जाता है तथा एसी प्राप्त अंक 3 या 3 के गुणज के अतिरिक्त हो तो एक सिक्के को उछाला जाता है। यदि घटना कम से कम एक पासे 3 पर प्रकट होना का घटित होना दिया गया है तो घटना ' सिक्के पर पट आना कि सप्रतिबंध प्रायिकता ज्ञात कीजिए।
View Solutionएक थैले में 10 सफ़ेद और 15 काली गेंदे है। दो गेंदे एक के बाद निकाली जाती है और पहली गेंद दूसरी के निकलने से पहले वापस नहीं रखी जाती है , तब पहली गेंद के सफ़ेद तथा दूसरी गेंद के काली होने कि प्रायिकता ज्ञात करो ।
View Solution52 पत्तो कि अच्छी तरह फेंटी गई ताश कि गड्डी में से एक - एक करके तीन पत्ते बिना प्रतिस्थापन के निकाले गए। इनमे से पहले दो पत्तो का बादशाह तथा तीसरे पत्ते का बेगम होने कि प्रायिकता ज्ञात करो ।
View Solutionघटनाएँ A तथा B इस प्रकार कि है कि `P(A) = 1/2 , P(B) = 7/12 ` तथा P(A - नहीं या B - नहीं ) `= 1/4` तब क्या A तथा B स्वतंत्र घटनाएँ है ?
View Solutionएक न्याय्य सिक्के और एक अनभिंत पासे को उछाला गया है। A माना घटना ' सिक्के पर चित प्रकट होना ' तथा B घटना ' पासे पर अंक 3 प्रकट होना ' को निरूपित करते है। निरीक्षण कीजिए कि घटनाएँ A और B स्वतंत्र है या नहीं ।
View Solutionएक पासे पर अंक1,2,3 लाल रंग से तथा4,5,6 हरे रंग से लिख गया है। इस पासे को उछाला गया है। माना A घटना अंक सम है तथा B घटना ' अंक लाल है ' को निरूपित करते है। क्या घटनाएँ A तथा B स्वतंत्र है ?
View Solutionएक पासे को एक बार उछाला गया है माना A घटना ' पासे पर प्राप्त अंक के 3 का गुणज होना ' तथा B घटना ' पासे पर प्राप्त अंक सम होना ' को निरूपित करते है। क्या घटनाएँ A तथा B स्वतंत्र है ?
View Solutionघटनाएँ A तथा B इस प्रकार है कि `P(A) = 1/2 , P ( A cup B ) = 3/ 5 ` तथा `P (B) = r` तब r ज्ञात कीजिए । यदि
ये घटनाएँ परस्पर अपजवर्ती है।
View Solutionघटनाएँ A तथा B इस प्रकार है कि `P(A) = 1/2 , P ( A cup B ) = 3/ 5 ` तथा `P (B) = r` तब r ज्ञात कीजिए । यदि
ये घटनाएँ स्वतंत्र है।
View Solutionतीन सिक्को को उछाला गया है। माना A घटना ' ती चित या तीन पर प्राप्त होना ' , B घटना ' कम से कम दो चित प्राप्त होना, ' तथा C घटना ' अधिकतम दो चित प्रपात होना ' को निरूपित करते है। ज्ञात कीजिये की निम्न युग्मो (A,B) , (A,C) तथा (B,C) में से कौन - कौन से स्वतंत्र है ? कौन - कौन से युग्म आश्रित है ?
View Solutionयदि किसी यादृच्छिक प्रयोग से सम्बद्ध A तथा B स्वतंत्र घटनाएँ है तो सिद्ध करो :
`bar(A)` तथा B स्वतंत्र घटनाएँ है ।
View Solutionयदि किसी यादृच्छिक प्रयोग से सम्बद्ध A तथा B स्वतंत्र घटनाएँ है तो सिद्ध करो :
A तथा`bar(B)` स्वतंत्र घटनाएं है
View Solutionयदि किसी यादृच्छिक प्रयोग से सम्बद्ध A तथा B स्वतंत्र घटनाएँ है तो सिद्ध करो :
`bar(A)` तथा `bar(B)` भी स्वतंत्र घटनाएँ है।
View Solutionयदि A तथा B स्वतंत्र घटनाएं हो तो कम से कम एक घटना के घटित होने की प्रायिकता ज्ञात करो ।
View Solutionकिसी कक्षा के दो तिहाई विद्यार्थी लड़के है तथा शेष लड़कियाँ है। किसी लड़की के प्रथम श्रेणी प्रपात करने की प्रायिकता `0.25` व लड़के के प्रथम श्रेणी प्रपात करने की प्रायिकता `0.28` है। तब यादृच्छया चुने गए किसी विद्यार्थी के प्रथम श्रेणी प्राप्त करने की परपायिकता ज्ञात करो।
View Solutionएक बोल्ट बनाने के कारखाने में मशीने ( यंत्र ) A , B और C कुल उत्पादन का क्रमशः 25 % , 35 % और 40 % बोल्ट बनाती है । इन मशीनों के उत्पादन का क्रमशः 5, 4 और 2 प्रतिशत त्रुटिपूर्ण है। बोलतो के कुल उत्पादन में से एक बोल्ट यादृच्छया निकाला जाता है और वह त्रुटिपूर्ण पाया जाता है । इसकी प्रायिकता है की यह बोल्ट मशीन B द्वारा बनाया जाता है ?
View Solutionतीन सर्वसम डिब्बे I,IIऔर III में एक सोने और एक चाँदी का सिक्का है। एक व्यक्ति यादृच्छया एक डिब्बा चुनता है और उसमे से एक सिक्का निकालता है । यदि निकाला गया सिक्का सोने का है तो इस बात की या प्रायिकता है की डिब्बे में दूसरा सिक्का भी सोने का है ?
View Solutionएक व्यक्ति के बारे में ज्ञात है कि वह 4 में से 3 बार सत्य बोलता यही। वह ऐसे पास को उड़ेलता है और बदलता है कि उस पर आने वाली संख्या 6 है । इसकी प्रायिकता ज्ञात कीजिए कि पासे पर आने वाली संख्या वास्तव में 6 है |
View Solutionमाना कि एक एच , आई , वी परीक्षण कि विश्वसनीयता निम्नलिखित प्रकार से निर्दिष्ट कि गई है। एच , आई , वी पोजिटिव व्यक्तियों के लिए परीक्षण 90 % पता लगाने में और 10 % पता न लगाने में सक्ष्म है । एच , आई , वी से स्वतंत्र व्यक्तियों के99 % लिए परीक्षण सही पता लगाता है यदि एच , आई , वी नेगेटिव बताता है जबकि 1 % परीक्षित व्यक्तयो के लिए एच , आई , वी जोजिटिव बताता है। एक बड़ी जनसँख्या , जिसमे `0.1` % व्यक्ति एच , आई , वी ग्रसित है , में से एक व्यक्ति यादृच्छया चुना जाता है और उस का परीक्षण किया जाने पर रोगविज्ञानी एच , आई , वी कि उपस्थिति बताता है क्या प्रायिकता है कि वह व्यक्ति वास्तव में एच , आई , वी ग्रस्त है ?
View Solutionएक यादृच्छिक चर का प्रायिकता बंटन नीचे दिया गया है -
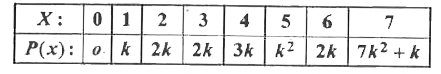
ज्ञात कीजिए -
(i) K
(ii) ` P ( x lt 6 ) `
(iii) ` P ( x ge 6)`
(iv) ` P (0 ltx lt 5)`
View Solutionताश के 52 पत्तो कि एक भली - भाँति फेंटी गई गड्डी में तीन पत्ते निकाले गए है । इक्को कि संख्या का प्रायिकता बंटन ज्ञात कीजिए।
View Solutionमाना किसी यादृच्छिक चुने गए विद्यालयी दिवस में पढाई के घंटो को X से दर्शाया जाता है । X के मान x लेने कि प्रायिकता निम्न है , जहाँ k एक अज्ञात अचर है ।
` P (X = x) = |{:(0.1 ," , यदि "x = 0 ),(kx," , यदि x = 1 या 2" ),(K (5-x)," ,यदि x= 3 या 4" ),(0," अन्यथा "):}`
k का मान ज्ञात करो ।
View Solutionमाना किसी यादृच्छिक चुने गए विद्यालयी दिवस में पढाई के घंटो को X से दर्शाया जाता है । X के मान x लेने कि प्रायिकता निम्न है , जहाँ k एक अज्ञात अचर है ।
` P (X = x) = |{:(0.1 ," , यदि "x = 0 ),(kx," , यदि x = 1 या 2" ),(K (5-x)," ,यदि x= 3 या 4" ),(0," अन्यथा "):}`
इस बात कि क्या प्रायिकता है कि आप
View Solutionमाना किसी यादृच्छिक चुने गए विद्यालयी दिवस में पढाई के घंटो को X से दर्शाया जाता है । X के मान x लेने कि प्रायिकता निम्न है , जहाँ k एक अज्ञात अचर है ।
` P (X = x) = |{:(0.1 ," , यदि "x = 0 ),(kx," , यदि x = 1 या 2" ),(K (5-x)," ,यदि x= 3 या 4" ),(0," अन्यथा "):}`
कम से कम दो घंटो पड़ते है ?
View Solutionमाना किसी यादृच्छिक चुने गए विद्यालयी दिवस में पढाई के घंटो को X से दर्शाया जाता है । X के मान x लेने कि प्रायिकता निम्न है , जहाँ k एक अज्ञात अचर है ।
` P (X = x) = |{:(0.1 ," , यदि "x = 0 ),(kx," , यदि x = 1 या 2" ),(K (5-x)," ,यदि x= 3 या 4" ),(0," अन्यथा "):}`
तथ्यतः दो घंटे पढ़ते है ?
View Solutionमाना किसी यादृच्छिक चुने गए विद्यालयी दिवस में पढाई के घंटो को X से दर्शाया जाता है । X के मान x लेने कि प्रायिकता निम्न है , जहाँ k एक अज्ञात अचर है ।
` P (X = x) = |{:(0.1 ," , यदि "x = 0 ),(kx," , यदि x = 1 या 2" ),(K (5-x)," ,यदि x= 3 या 4" ),(0," अन्यथा "):}`
अधिकतम दो घंटे पढ़ते है ?
View Solutionएक सिक्के को इस प्रकार अभिनत किया गया है कि सिक्के पर चित आने कि संभावना पट आने कि अपेक्षा तीन गुना है। यदि सिक्के को दो बार उछाला जाता है तो पीटीओ कि संख्या के लिए प्रायिकता बंटन ज्ञात करो।
View Solutionतीन सिक्को को एक साथ उछाला गया है। सिक्को पर चितो कि संख्या को यादृच्छिक चर X मानते हुए X का माध्य ज्ञात कीजिए ।
View Solutionताश के 52 पत्तो कि एक अच्छी प्रकार से फेंटी गई गड्डी में से दो पत्ते प्रतिस्थापन के साथ निकाले जाते है । इक्को कि संख्या का प्रायिकता बंटन तथा माध्य ज्ञात कीजिए ।
View Solutionदो पासो को एक साथ उछाला गया है। यदि X अंक छः कि संख्याओं को व्यक्त करता हो तो X का प्रसारण ज्ञात करो।
View Solutionप्रथम छः घनपूर्णांको में से दो संख्याओं यादृच्छया ( बिना प्रतिस्थापन ) चुनी जाती है माना दोनों संख्याओं में से बड़ी संख्या को व्यक्त करता है । जब X का प्रसरण ज्ञात करे।
View Solutionएक कक्षा में 15 छात्र है जिसकी आयु 14,17,15 21,17,19,20 , 16,18,20,17,16,19, और 20 वर्ष है । एक छात्र को इस प्रकार चुरा गया है प्रत्येक क्षात्र के चुने जाने कि संभावना समान है और चुने गए छात्र कि आयु X को लिखा गया । यादृच्छिक चर X का प्रायिकता बंटन क्या है ? X का माध्य , प्रसरण व मानक विचलन ज्ञात कीजिए।
View Solutionपासो के एक जोड़े को 7 बार फेंका गया है। यदि ' पासो ' पर प्राप्त अंको का योग 7 होना सफलता मानी जाए तो क्या प्रायिकता है :
कोई सफलता नहीं
View Solutionपासो के एक जोड़े को 7 बार फेंका गया है। यदि ' पासो ' पर प्राप्त अंको का योग 7 होना सफलता मानी जाए तो क्या प्रायिकता है :
छः सफलताएँ
View Solutionपासो के एक जोड़े को 7 बार फेंका गया है। यदि ' पासो ' पर प्राप्त अंको का योग 7 होना सफलता मानी जाए तो क्या प्रायिकता है :
कम से कम छः सफलताएँ
View Solutionपासो के एक जोड़े को 7 बार फेंका गया है। यदि ' पासो ' पर प्राप्त अंको का योग 7 होना सफलता मानी जाए तो क्या प्रायिकता है :
अधिकतम छः सफलताएँ
View Solutionएक अनभिनत पासे को एक बार - बार तब तक उछाला जाता है। जब तक की उस पर 6 का अंक तीन बार प्राप्त नहीं हो जाता। इस बात की क्या प्रायिकता है की पासे पर तीसरा 6 का अंक उसे छठी बार उछालने पर प्राप्त होता है।
View Solutionएक न्याय्य सिक्के को 5 बार उछाला गया है । कम से कम 3 चित प्राप्त करने की प्रायिकता ज्ञात कीजिये।
View Solutionएक पासे को 6 बार उछाला गया है। यदि 'पासे पर विषम संख्या प्राप्त होना' एक सफलता है तो निमंलिखित कि प्रायिकताएन क्या होंगी?
(i) तथ्यत: 5 सफलताएँ
(ii) कम से कम 5 सफलताएँ
(iii) अधिकतम 5 सफलताएँ।
View Solutionएक व्यक्ति के लक्ष्य भेदन की प्रायिकता `1/4` है। यह कम - से - कम कितनी बार गोली चलाए की लक्ष्य को कम से कम एक बार भेदने की प्रायिकता `2/3` से अधिक हो ?
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता `0.4` तथा एक कदम पीछे हटने की प्रायिकता `0.5` है। इस बात की क्या प्रायिकता है ग्यारह कदमो के पश्चात वह व्यक्ति शुरुआती बिंदु से के कदम दूर है ?
View SolutionA और B एकांतरतः एक पासे के जोड़े को उछलते है। यदि B के 7 फेंकने से पहले A 6 फेंकता है तब A जीतता है तथा यदि A 6 फेंकने से पहले B,7 फेंकता है तब B जीतता है। यदि A के जितने की प्रायिकता ज्ञात करो ।
View Solutionयदि एक द्वितीय क्रम के सारणिक का प्रत्येक अवयव शून्य या एक हो तो सारणिक का मान धनात्मक होने की क्या प्रायिकता है ? ( यह मानते हुए कि सरणिक के प्रत्येक अवयव को स्वतंत्र रूप से चुना जा सकता है तथा प्रत्येक के चुने जाने कि प्रायिकता `1/2 ` है । )
View Solutionद्विपद बंटन `B (4,1/3)` का माध्य ज्ञात कीजिये ।
View Solution
पाठ्य पुस्तक के उदाहरण questions and complete solutions for chapter प्रायिकता एवं प्रायिकता बंटन of MITTAL MATHS (HINDI) of Class 12
All Exercises from MITTAL PUBLICATION Class 12 MATHS प्रायिकता एवं प्रायिकता बंटन
- CHECK YOUR POTENTIALITY
- COMPETITION CORNER
- LAST YEARS BOARD QUESTIONS
- PRACTICE QUESTIONS
- अभ्यासार्थ प्रश्नावली 16.1
- अभ्यासार्थ प्रश्नावली 16.2
- अभ्यासार्थ प्रश्नावली 16.3
- अभ्यासार्थ प्रश्नावली 16.4
- अभ्यासार्थ प्रश्नावली 16.5
- पाठ्य पुस्तक के उदाहरण
- पाठ्य पुस्तक प्रश्नावली 16.1
- पाठ्य पुस्तक प्रश्नावली 16.2
- पाठ्य पुस्तक प्रश्नावली 16.3
- पाठ्य पुस्तक प्रश्नावली 16.4
- पाठ्य पुस्तक प्रश्नावली 16.5
- विविध प्रश्नावली 16 (पाठ्य पुस्तक )
- साधित उदाहरण