Complete Solutions to EXERCISE of chapter SAMPLE PAPER 2016 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | SAMPLE PAPER 2016 |
| MODERN PUBLICATION | EXERCISE |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
Write that condition of Rolle’s theorem which is violated by the function `f(x)=|x-1|` in `[0,2]`.
View SolutionWrite the value of `int_0^(pi/2)(sinx)/(sinx+cosx)dx-int_0^(pi/2)(cosx)/(sinx+cosx)dx`
View SolutionIf p and q are the order and degree of the differential equation `y(dy/dx)^2+x^2(d^2y)/dx^2+xy=sinx,` then choose the correct statement out of (i) `pgtq`, (ii) `p=q`, (iii) `pltq`.
View SolutionIf `|vec(a)|=3,|vec(b)|=2` and `vec(a)*vec(b)=0`, then write the value of `|vec(a)xxvec(b)|`.
View SolutionWrite the distance between parallel planes `2x-y+3z=4` and `2x-y+3z=18`.
View SolutionWrite the equation of the sphere concentric with the sphere `x^2+y^2+z^2-4x-2x-2y+2z-30=0` and passing through the origin.
View SolutionIf A is a `4xx5` matrix and B is a matrix such that `A^TB` and `BA^T` both are defined, then write the order of B.
View SolutionIf `""^nC_r=^nP_r,r!=1`, then write the value of r.
View SolutionA binomial distribution has mean `4` and variance `3`. Write the number of trials.
View SolutionFind `(dy)/(dt)`, when `y=sin^(-1)(2sqrt(t^(2)-1)/(t^(2)))`
View SolutionFind dy/dx if
`x^m y^n = (x/y)^(m+n)`
View SolutionIf `x=asec theta, y=b tan theta`, then prove that `(d^(2)y)/(dx^(2))=-(b^(4))/(a^(2)y^(3))`
View Solutionif `u=x^3-3xy^2`, show that
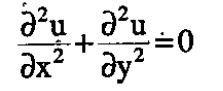
View SolutionFind the interval where the following function is increasing:
`y=sinx+cosx`, `x epsilon [0,2pi].`
View SolutionFind the following limits:`lim_(xrarr0+)(ln tanx)/(ln sin 2x)`
View SolutionThe radius of a spherical soap bubble is increasing at the rate of 0.2 cm`//`sec. Find the rate of increase of its surface area, when the radius is 7 cm. (`pi` = 3.141 approx)
View SolutionIf `f'(x)=e^x+1/(1+x^2)` and `f(0)=1,` then find f(x).
View SolutionEvaluate : `int(logx)^2dx`
View SolutionEvaluate: `int(2x+9)/(x+3)^2dx`
View Solution`int_0^1(x^5(4-x^2))/sqrt(1-x^2)dx`
View SolutionEvaluate `int (sin x cos x)/(sin^2x- 2sin x+3) dx`
View SolutionSolve `dy + e^-y sin x dx = 0`.
View SolutionSolve: `(x^2-1)dy/dx+2xy=1`
View SolutionProve that
`|a+b| le |a| + |b|`
State when equality will hold,
View SolutionFind the area of the triangle ABC with vertices A(1,2,4), B(3,1,-2) and C(4,3,1) by vector method.
View SolutionFor any three vectors veca,vecb,vecc show that `[(veca-vecb) (vecc-veca) (vecb-vecc)] = 0`
View SolutionThe projection of a line segment `overline(OP)`, through origin O, on the co-ordinate axes are 6, 2, 3. Find the length of the line segment OP and its direction cosines.
View SolutionFind the equation of the plane passing through the point (-1,3,2) and perpendicular to the planes `x+2y+2z=5` and `3x+3y+2z=8`.
View SolutionProve that the lines `(x+4)/3=(y+6)/5=(z-1)/(-2)` and `3x-2y+z+5=0=2x+3y+4z-4` are co-planar.
View SolutionSolve the following LPP graphically
Maximize, `Z=20x+30y`
Subject to `3x+5yle15`
`x,yge0`.
View SolutionFind the feasible region of the following system
`2x+yge6,x-yle3,xge0,yge0`
View SolutionShow that `(a+1)` is a factor of `abs([(a+1),2,3],[1,a+1,3],[3,-6,a+1])`
View SolutionProve that the following. `[[a,b,c],[x,y,z],[p,q,r]]=[[y,b,q],[x,a,p],[z,c,r]]=[[x,y,z],[p,q,r],[a,b,c]]`
View SolutionIf `A=[[alpha,0],[1,1]]` and `B=[[1,0],[5,1]]`, show that for no values of `alpha, A^2=B`.
View SolutionHow many 4 digit numbers each greater than 6000 can be formed with be digits 5, 6, 7 and 8?
View SolutionIf `m=""^nC_2`, prove that `""^nC_2=3(n+1)C_4`.
View SolutionIf the ratio of the 3rd term from the beginning to the 3rd term from the end in the expansion of `(1+sqrt2)^n` is `1/8`, then find the value of n.
View SolutionLet A and B be events with `P(A)=1/3,P(AuuB)=3/4,P(AnnB)=1/4`, find `P(AuuB^C)`.
View SolutionIf X follows a binomial distribution with parameter `n=6` and p with `4P(X=4)= P(X=2)`, find p.
View SolutionIf `x = (1-cos^2 theta)/(cos theta), y = (1-cos^(2n)theta)/(cos^n theta)` then show that `(dy/dx)^2 = n^2((y^2 + 4)/(x^2 +4))`
View SolutionShows that the triangle of greatest area that can be inscribed in a circle is equilateral.
View SolutionDetermine the area common to the parabola `y^2=x` and the circle `x^2+y^2=2x`.
View SolutionFind the solution of the following differential equations:
`x dy-ydx=sqrt(x^2+y^2)dx`
View SolutionProve that `vecaxx(vecbxxvecc)+ vecbxx(veccxxveca)+veccxx(vecaxxvecb)` = 0 and hence prove that `vecaxx(vecbxxvecc), vecbxx(veccxxveca), veccxx(vecaxxvecb)` are coplanar.
View SolutionA variable plane meets the coordinate axes at P, Q, R points. If the plane passes through a fixed point (a, b, c), prove that the centre of the shpere passing the origin and P, Q, R will lie on the surface `a/x+b/y+c/z=2`
View SolutionSolve the following LPP graphically Maximize `z=5x_1+3x_2`
Subject to `3x_1+5x_2le15
,5x_1+2x_2le10
,x_1, x_2ge0`.
View SolutionSolve the following system of equations by the matrix inversion method.
`x+y+z=4`
`2x-y+3z=1`
and `3x+2y-z=1`
View SolutionThree persons hit a target with probabilities `(1/2)`,`(1/3)` and `(1/4)` respectively. If each one shoots at the target once, (i) find the probaility that exactly one of them hits the target, (ii) if only one of them hits the target what is the probability that it was the first person?
View Solution
EXERCISE questions and complete solutions for chapter SAMPLE PAPER 2016 of MODERN PUBLICATION of Class 12