Complete Solutions to Objective Type Questions (D. Very Short Answer Types Questions) of chapter RELATIONS AND FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| MODERN PUBLICATION | Objective Type Questions (D. Very Short Answer Types Questions) |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
Let `A={1,2,3,4}`. Let R be the equivalence relation on `AxxA` defined by `(a,b)R(c,d)` iff `a+d=b+c`. Find `{(1,3)}`.
View SolutionIf `R={(1,-1),(2,-2),(3,-1)}` is a relation, then find the range of R.
View SolutionIf `R={(x,y):x+2y=10}` is a relation in N, write the range of R.
View SolutionGive an example of a relation which is reflexive and symmetric but not transitive.
View SolutionGive an example of a relation which is transitive but neither reflexive nor symmetric.
View SolutionLet R be the relation ''greater than'' from `A={1,4,5}` to `B={1,2,4,5,6,7}`. Write down the elements corresponding to R.
View SolutionWhich one of the following graphs represents the function of x? why?
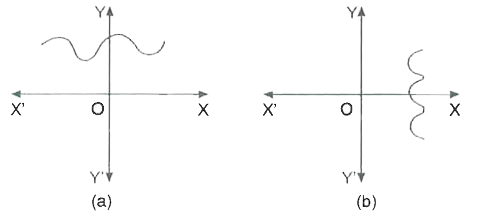
View SolutionShow that `f(x)=3x+5` for all `xinQ`, is one-one.
View SolutionShow that the function `f: N->N` , given by `f(x)=2x` , is one-one but not onto.
View SolutionIf f is a function from `RrarrR` such that `f(x)=x^(2)AA x inR`, then show that 'f' is not one-one.
View SolutionLet `A = {1, 2, 3}`, `B = {4, 5, 6, 7}`and let `f = {(1, 4), (2, 5), (3, 6)}`be a function from A to B. Show that f is one-one.
View SolutionThe function P is defined as:
''To each person on the earth is assigned a date of birth''. Is this function one-one? Give reason.
View SolutionWrite the function whose graph is shown below:
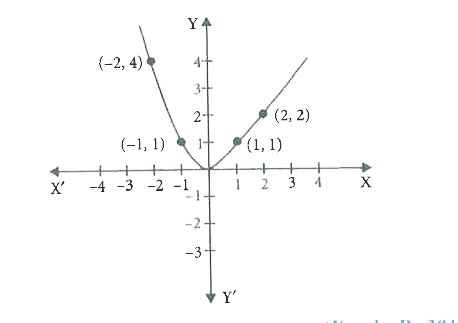
View SolutionConsider functions f and g such that composite gof is defined and is one-one. Are f and g both necessarily one-one.
View SolutionAre f and g both necessarily onto, if `gof`is onto?
View SolutionGive examples of two functions `f:" "N->Z" "a n dg:" "Z->Z` such that o f is injective but is not injective. (Hint: Consider `f(x)" "=" "x" "a n d""""""""g(x)" "=" "|x|` )
View SolutionGive examples of function:
`f:NrarrN and g:NrarrN`
such that gof is onto but f is not onto.
View SolutionFind fog, if `f:RrarrR` and `g:RrarrR` are given by:
`f(x)=cosxandg(x)=x^(2)`.
View SolutionIf f (x) = sin x, g(x) = `x^(2)`, if `x inR`, then find [(fog)(x)].
View SolutionIf `f:RrarrR` is defined by `f(x)=3x+1`, find `f(f(x))`.
View SolutionLet `'**'` be a binary operation on N given by:
`a**b=LCM (a,b)` for all `a, b inN`.
Find `6**7`
View SolutionLet `'**'` be a binary operation on N given by:
`a**b=LCM (a,b)` for all `a, b inN`.
Find `20**16`
View SolutionThe binary operation `**:RxxRrarrR` is defined as:
`a**b=2a+b`.
Find `(2**3)**5`.
View SolutionShow that `+ : R xx R ->R`and `xx : R xx R ->R`are commutative binary operations, but ` : RxxR ->R`and `-: : R_* xxR_* ->R_*`are not commutative.
View SolutionShow that `+ : R xx R ->R`and `xx : R xx R ->R`are commutative binary operations, but ` : RxxR ->R`and `-: : R_* xxR_* ->R_*`are not commutative.
View SolutionShow that addition and multiplication are associative binary operation on R. But subtraction is not associative on R. Division is not associative on R*.
View SolutionShow that subtraction and division are not binary operations on N.
View SolutionShow that `" "a` is not the inverse of `a in N` for the addition operation + on N and `1/a` is not the inverse of `a in N` for multiplication operation `xx` on N, for `a!=1` .
View SolutionShow that `" "a` is not the inverse of `a in N` for the addition operation + on N and `1/a` is not the inverse of `a in N` for multiplication operation `xx` on N, for `a!=1` .
View Solution
Objective Type Questions (D. Very Short Answer Types Questions) questions and complete solutions for chapter RELATIONS AND FUNCTIONS of ARIHANT MATHS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 MATHS RELATIONS AND FUNCTIONS
- CHAPTER TEST (1)
- CHECK YOUR UNDERSTANDING
- COMPETITION FILE (Questions from JEE Main)
- Exercise
- EXERCISE 1 (a) (Long Answer Type Questions (I))
- EXERCISE 1 (a) (Long Answer Type Questions (II))
- EXERCISE 1 (a) (Short Answer Type Questions)
- EXERCISE 1 (b) (Long Answer Type Questions (I))
- EXERCISE 1 (c) (Long Answer Type Questions (I))
- EXERCISE 1 (c) (Short Answer Type Questions)
- EXERCISE 1 (d) (Long Answer Type Questions (I))
- EXERCISE 1 (d) (Short Answer Type Questions)
- EXERCISE 1 (e) (Long Answer Type Questions (I))
- EXERCISE 1 (e) (Short Answer Type Questions)
- FREQUENTLY ASKED QUESTIONS
- ILLUSTRATIVE EXAMPLES
- Misellaneous Exercise on Chapter (1)
- NCERT - FILE (Question from NCERT Book) (Exercise 1.1)
- NCERT - FILE (Question from NCERT Book) (Exercise 1.2)
- NCERT - FILE (Question from NCERT Book) (Exercise 1.3)
- NCERT - FILE (Question from NCERT Book) (Exercise 1.4)
- Objective Type Questions (A. Multiple Choice Questions)
- Objective Type Questions (B. Fill in the Blanks)
- Objective Type Questions (C. True/False Questions)
- Objective Type Questions (D. Very Short Answer Types Questions)
- QUESTIONS FROM NCERT EXEMPLAR
- Revision Exercise