Complete Solutions to Objective Type Questions (A. Multiple Choice Questions) of chapter INVERSE - TRIGONOMETRIC FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | INVERSE - TRIGONOMETRIC FUNCTIONS |
| MODERN PUBLICATION | Objective Type Questions (A. Multiple Choice Questions) |
| Number Of Questions | 26 |
| Academic Year | 2023-24 |
If `Sin^(-1)x=y`, then
View Solution`tan^(-1)(sqrt(3))+sec^(-1)(-2)`=
View Solution`cos^(-1)(cos((7pi)/6))` is equal to
View Solution`sin(pi/3-sin^(-1)(-1/2))`is equal to(A) `1/2` (B) `1/3` (C) `1/4` (D) 1
View Solution`tan^(-1)sqrt(3)-cot^(-1)(-sqrt(3))`is equal to
View Solution`sin(tan^(-1)x),|x| le 1` is equal to :
View Solution`sin^(-1)(1-x)-2 sin^(-1)x=(pi)/(2)`, then x is equal to
View Solution`tan^(-1)(x/y)-tan^(-1)(x-y)/(x+y)`is equal to(A) `pi/2` (B) `pi/3` (C) `pi/4` (D) `(-3pi)/4`
View SolutionThe value of ` sin^(-1) (cos ((43pi)/5))` is :
View SolutionThe principal value of the expression : `cos^(-1) [ cos (-680^(@))] ` is :
View SolutionThe value of `cot(sin^(-1) x ) ` is :
View SolutionThe domain of `sin^(-1) 2x ` is :
View Solutionthe greatest and least values of `(sin^(-1) x)^2+(cos^(-1)x)^2`
View SolutionThe principal value of `sin^(-1)(1/2)` is
View Solution`tan^(-1)sqrt(3)-cot^(-1)(-sqrt(3))`is equal to(A) `pi` (B) `-pi/2` (C) 0 (D) `2sqrt(3)`
View Solution`cos^(-1)(cos((7pi)/6))` is equal to
View Solution`sin(pi/3-sin^(-1)(-1/2))`is equal to(A) `1/2` (B) `1/3` (C) `1/4` (D) 1
View Solution`sin(pi/3-sin^(-1)(-1/2))`is equal to
View SolutionFind the principal value of: `sin^(-1)(-1/2)`
View SolutionIf `cos^(-1) x = y ` then :
View SolutionFind the principal value of `sin^(-1)``(1/(sqrt(2)))`
View SolutionThe value of `sin(cos^(-1)3/5)` is
View SolutionIdentify the function from the following figure :
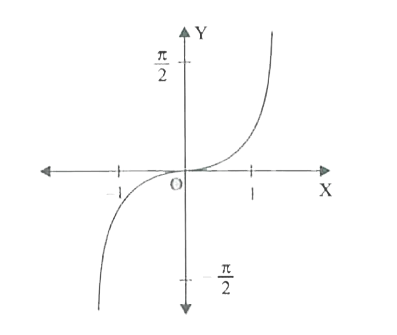
View SolutionFind the principal value of `cot^(-1)``((-1)/(sqrt(3)))`.
View SolutionPrincipal value of `cos^(-1)[cos((4pi)/(3))]` is
View SolutionThe principle value of `sin ^(-1)(sin ""(2pi)/(3))` is
View Solution
Objective Type Questions (A. Multiple Choice Questions) questions and complete solutions for chapter INVERSE - TRIGONOMETRIC FUNCTIONS of ARIHANT MATHS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 MATHS INVERSE - TRIGONOMETRIC FUNCTIONS
- CHAPTER TEST (2)
- CHECK YOUR UNDERSTANDING
- COMPLETITION FILE (Questions from JEE Main)
- Exercise
- EXERCISE 2 (a) (Long Answer Type Questions )
- EXERCISE 2 (a) (Short Answer Type Questions)
- EXERCISE 2 (b) (Long Answer Type Questions (II))
- EXERCISE 2 (b) (Short Answer Type Questions)
- Frequently Asked Questions
- ILLUSTRATIVE EXAMPLES
- Misellaneous Exercise on Chapter (2)
- NCERT - FILE (Question from NCERT Book) (Exercise 2.1)
- NCERT - FILE (Question from NCERT Book) (Exercise 2.2)
- Objective Type Questions (A. Multiple Choice Questions)
- Objective Type Questions (B. Fill in the Blanks)
- Objective Type Questions (C. True/False Questions)
- Objective Type Questions (D. Very Short Answer Types Questions)
- Questions From NCERT Exemplar
- Revision Exercise